Team:TU-Delft/Project/Modelling

</html>

Results

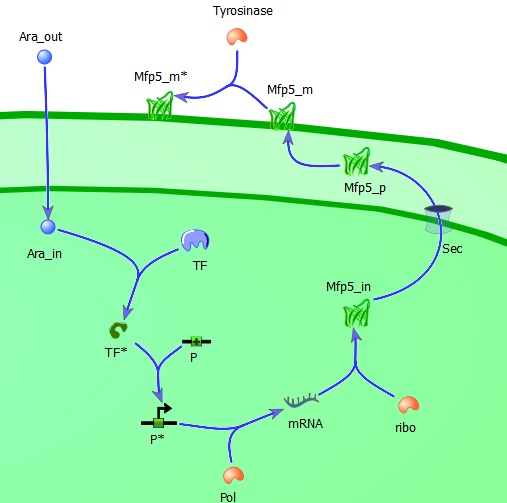
The Cluster model

The Regulatory Model

Description:

To perform simulations, a numerical ordinary differential equation solver of MatLab was used (ode45). As mentioned in a previous section the model includes several assumption, mainly based on mechanisms described in literature (Alon, 2007). Following hypotheses were used to derive a mechanistic model for the production and transport of Mfp-5.

'The tansport of arabinose (the inducer) across the inner cell membrane is based on diffusion kinetics.'

Under normal conditions, arabinose is transported into E.coli via arabinose permeases (AraE and AraFGH) (Khlebnikov et al., 2000). Because no kinetic mechanisms for the transport were available, the transport was simplified to a diffusion mechanism over the two membranes. The diffusion coefficient was based on literature; diffusion coefficient for small molecules (Alon, 2007). The assumed concentration of inducer (Carabinose_out = 55E-5 mol/L) was shown as optimal inducer concentration (Nanninger et al., 2010). The following relation was used to calculate the rate of diffusion (v_arabinose) in time (Fick’s Law):

v_arabinose= -Diff.coef_arabinose*((〖C_arabinose〗_in- C_(arabinose_out )))/(d_(membrane_tot )*10E-5)

The concentration of arabinoseout is given, as shown by literature. The thickness of the membrane, d_(membrane_tot )=0.021 µm is calculated by addition of the inner-membrane, outer-membrane and periplasm (Mitra et al., 2004)(Graham et al., 1991)(Abramson et al., 2003). Per iteration the 〖C_arabinose〗_in will increase, until steady state is reached, as described in the following equation:

C_(arabinose_in )= v_arabinose*A_cell/V_cell

In this equation, the volume of the cell equals 1 µm3 (Kubitschek et al., 1986) and the surface of the cell is calculated. Assumed is a spherical cell, whereupon Acell can be calculated by 4πR2, with R = ∛((V_cell*(3/4))/π) .

'Production of AraC and Mfp-5: protein production.'

When the arabinose in transported in the cell, first this will bind to the AraC-gene. This is the gene for the production of the transcription factor. After the transcription factor is produced, this will bind to the mfp-5 promoter , in order to produce the mfp-5 protein. The AraC-protein as well as the Mfp-5 protein are assumed to follow similar processes: the production of a protein. This production is divided into two steps; first transcription (copying DNA to mRNA, messenger RNA ) whereupon translation follows. Translation means the translation of mRNA to amino The following relations were assumed (Alon, 2007):

Transcription : the production of mRNA

During the production of mRNA , several assumptions are taken into account. In order to transcribe a gene, a certain amount of inducer is required, assumed is that one molecule arabinose activates one gene, thus N =1 (Khlebnikov et al., 2000). Since we inserted a high copy vector, there are several copies of the AraC gene present, which was assumed to be 100 AraC genes (=N_cAraC). Per transcription, a RNA-polymerase performs the transcription at a certain speed Rtrans = 80 nt/s (Bremer et al., 1996) and assumed is one active RNA polymerase per gene (=nPolyAraC). Given these assumptions, the maximum produced mRNA for AraC could be calculated by:</br>
β_mRNAmax_AraC= R_trans/756*N_cAraC*nPolyAraC*10E-9

The change in the maximum produced mRNA of Arac is directly related to the inducer concentration, assuming the Hill equation rate (Alon, 2007), where K_araC is the activation coefficient (=C_(arabinose_out )) and N = 1 as described above.
β_(mRNA_AraC )= β_(mRNAmax_AraC )*(C_arabinose_in)/(〖K_AraC〗^N+〖C_arabinose_in〗^N )

Since mRNA is rather unstable, it will degrade with a factor α_(mRNA_AraC ). α_(mRNA_AraC ) = log(2) / THalf life time mRNA, with Thalf life time mRNA= 4 min (Taniguchi Y. et al, 2010). Therefore, the rate of change (per iteration) in mRNA of AraC is described as:

 		          (dC_(mRNA_AraC ))= β_(mRNA_AraC )- α_(mRNA_AraC )*C_(mRNA_AraC )

Translation: the production of the protein, mRNA to protein

Given the calculated amount mRNA, the related amount of produced protein can be calculated, based on the same principle. Per strand mRNA several translation will be performed, pAraC = 10 (Alon, 2007). At steady state, a constant amount of mRNA will be produced and degraded, meaning C_(mRNA_AraC ) is constant if this is equal to β_(mRNA_AraC )/(α_(mRNA_AraC ) ). Multiplying these two factors, will lead to the concentration of ArAC protein. However, the AraC protein will also partly degrade, leading to the following equation to describe the production rate of Arac protein (Alon, 2007):

(dc_AraC) =p_AraC*  β_(mRNA_AraC )/(α_(mRNA_AraC )  )–α_(p_AraC )*C_AraC

The α_(p_AraC ) is calculated by log(2)/ THalf time AraC, with THalf time ArAC = 2 min (Kolodubretz et al., 1981). The production of Mfp-5 is assumed to be similar in process, only varying the half life time of the Mfp-5 protein, which is 10 min (Haemers, 2003)

'Transport of Mfp-5'

Mfp5 is transported via an active mechanism. Because no kinetic mechanisms for the transport were available, the transport was simplified to a diffusion mechanism over the two membranes. The mechanism was as described in the transport of the inducer arabinose leading to the following equations (Fick’s Law):
Transport over inner membrane:

The rate of diffusion through the inner membrane is given by:

v_(Mfp5_inner )= -Diff.coef_(Mfp5_inner)*(((C_(p_(Mfp5_peri ) )- C_(〖p_Mfp5〗_in )))⁄V_peri )/(x_(m_in )*10E-5)

Assuming Mfp5 to be a small molecule, the diffusion coefficient is assumed to be 1E-12 µm2/s (alon, 2007). Since the cell is assumed to have a spherical shape, one could calculate the volume of the periplasm and the volume of the outer membrane, if the volume of the cell as well as the diameters of the membranes and periplasm are known. The volume of the cell is 1 µm3 (Kubitschek et al., 1986), the diameter of the inner membrane is 4 µm and the diameter of the outer membrane is assumed 8 µm (Mitra et al., 2004)(Graham et al., 1991)(Abramson et al., 2003). The concentration in the periplasm can be calculated as follows:

C_(Mfp5_periplasm )= v_(Mfp5_inner )*A_(innermembrane_periplasm)/V_periplasm

Transport over outer membrane:

Assuming the given values above, the rate of diffusion through the outer membrane is given by:

v_(Mfp5_outer)= -Diff.coef_(Mfp5_outer)*(((C_(p_(Mfp5_out ) )- C_(〖p_Mfp5〗_peri )))⁄V_(mem_out ) )/(x_(m_out )*10E-5

Whereupon the concentration Mfp-5 integrated in the outer membrane can be calculated as follows:

C_(Mfp5_periplasm )= v_(Mfp5_inner )*A_(periplasm_outer)/V_(outer_membrane )

The arabinose concentration outside the cell was 55 E-5 mol/L, a relatively high concentration, which is expected to cause a high production rate of the protein. (Kleinschmidt et al. (1996)) The maximal produced mfp-5 was produced after 750s. A maximal mfp-5 concentration of 0.038 mmol/L was determined.

The Matlab Code: