Team:TU-Delft/Project/Modelling
From 2011.igem.org
(→The Regulatory Model) |
(→The Regulatory Model) |
||
| Line 49: | Line 49: | ||
=== The Regulatory Model === | === The Regulatory Model === | ||
| - | + | ====Description==== | |
To perform simulations, a numerical ordinary differential equation solver of MatLab was used (ode45). | To perform simulations, a numerical ordinary differential equation solver of MatLab was used (ode45). | ||
Revision as of 20:45, 30 January 2012








-
 Home
Home
-
 The Project
What we are doing
The Project
What we are doing
-
 The Team
Who we are
The Team
Who we are
-
 Notebooks
What we did
Notebooks
What we did
-
 Human Practice
Awareness
Human Practice
Awareness
-
 Safety
Responsibilty
Safety
Responsibilty
Modelling
Our project revolves around the addition of adhesive properties to Escherichia coli in a controlled manner. Adding the property may be regarded as the scientific part of our project, the control of the system is the engineering part. Modelling is our bridge between science and engineering. Using the scientific knowledge on our system, we can describe how the system will act and interact. Combining our mathematical model(s) with our lab results will lead to anas much realistic as possible description of our constructs and its possibilities. This description can then be used for predicting what will happen when you control the system using a specific parameter. Modelling offers the first answers to the questions posed when one engineers.
In our case, these questions are:
- How adhesive is the cell?
- How is adhesiveness dependent on induction of Mfp5?
- How do adhesive cells behave in a growth medium?
As mentioned above, to answer these questions we need to have a mechanical model. The mechanical description of the biological processes namely lays the foundation of understanding, as well as determines the framework of relations to be used in the model. We have separated the system in two parts: the intracellular (regulatory) module and the intercellular module
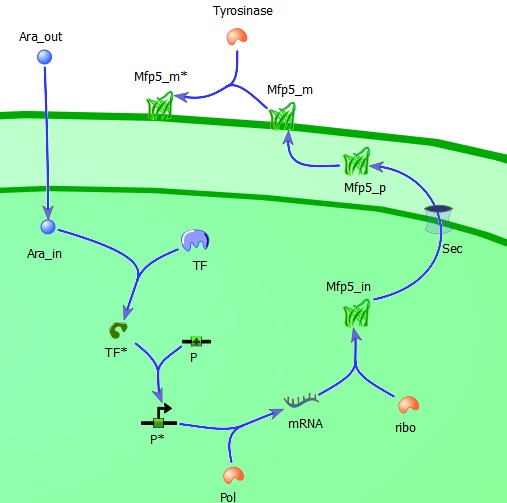
The intracellular module gives us information about the adhesiveness of Mfp-5 on the membrane which is directly dependent on the inducer (L-arabinose) concentration. It includes all steps in between the inducer (induction of the Mfp-5 expression?) and the amount of Mfp-5 eventually present on the outer membrane, such as for example the influence of the transcription factor, the efficiency of DNA-polymerase and the ribosome concentration in relation to the specific growth rate μ.
Extracellular L-arabinose (Ara_out) is transported inside the cell (Ara_in). Here it binds to the transcription factor (TF) which becomes active (TF*) and binds to the promotor (P). The active promotor (P*) is transcribed by DNA-polymerase (pol) and the resulting mRNA is translated by ribosomes (ribo) into intracellular Mfp5-GFP-OmpA (Mfp5_in). This is transported by the Sec transport system to the periplasm. The periplasmic Mfp5-GFP-OmpA (Mfp5_p) folds and inserts itself into the outer membrane (Mfp5_m). When tyrosinase is present tyrosine groups will be hydroxylated to L-DOPA groups resulting in adhesive membrane-bound Mfp5-GFP-OmpA (Mfp5_m*).
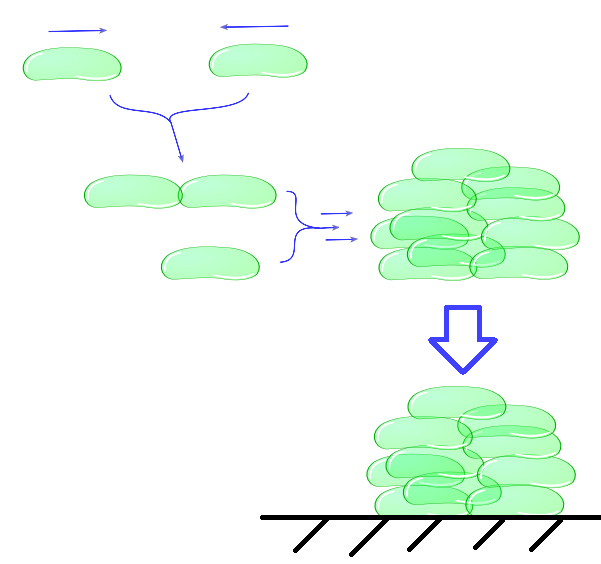
The intercellular module gives us information about cell physiology dependent on cell adhesiveness and environmental parameters. With this part of our model, we try to predict cell clustering and its related settling time. This includes factors as buoyancy, cluster formation and degradation, growth and death.(etc. not necessary because you say “includes”). In the end, our intracellular module will lead to a useful output, namely the adhesive properties of Mfp-5 in relation to the inducer. This output is directly the input for the intercellular model. Combination of as well the intracellular as the intercellular models enables us to predict the behaviour of cells in a growth medium, which is directly dependent on the concentration of the inducer L-arabinose.Individual cells bump into eachother and depending on adhesive strength of the Mfp5 and its concentration they will attach to form a larger cluster. This continuous clustering results into large heavy clusters with a high volume to surface ratio increasing their settling rate.
</br>
</html>
Results
The Cluster model
The Regulatory Model
Description
To perform simulations, a numerical ordinary differential equation solver of MatLab was used (ode45). As mentioned in a previous section the model includes several assumption, mainly based on mechanisms described in literature (Alon, 2007). Following hypotheses were used to derive a mechanistic model for the production and transport of Mfp-5.
The tansport of arabinose (the inducer) across the inner cell membrane is based on diffusion kinetics.
Under normal conditions, arabinose is transported into E.coli via arabinose permeases (AraE and AraFGH) (Khlebnikov et al., 2000). Because no kinetic mechanisms for the transport were available, the transport was simplified to a diffusion mechanism over the two membranes. The diffusion coefficient was based on literature; diffusion coefficient for small molecules (Alon, 2007). The assumed concentration of inducer (Carabinose_out = 55E-5 mol/L) was shown as optimal inducer concentration (Nanninger et al., 2010). The following relation was used to calculate the rate of diffusion (v_arabinose) in time (Fick’s Law):
v_arabinose= -Diff.coef_arabinose*((〖C_arabinose〗_in- C_(arabinose_out )))/(d_(membrane_tot )*10E-5)
The concentration of arabinoseout is given, as shown by literature. The thickness of the membrane, d_(membrane_tot )=0.021 µm is calculated by addition of the inner-membrane, outer-membrane and periplasm (Mitra et al., 2004)(Graham et al., 1991)(Abramson et al., 2003). Per iteration the 〖C_arabinose〗_in will increase, until steady state is reached, as described in the following equation:
C_(arabinose_in )= v_arabinose*A_cell/V_cell
In this equation, the volume of the cell equals 1 µm3 (Kubitschek et al., 1986) and the surface of the cell is calculated. Assumed is a spherical cell, whereupon Acell can be calculated by 4πR2, with R = ∛((V_cell*(3/4))/π) .
Production of AraC and Mfp-5: protein production.
When the arabinose in transported in the cell, first this will bind to the AraC-gene. This is the gene for the production of the transcription factor. After the transcription factor is produced, this will bind to the mfp-5 promoter , in order to produce the mfp-5 protein. The AraC-protein as well as the Mfp-5 protein are assumed to follow similar processes: the production of a protein. This production is divided into two steps; first transcription (copying DNA to mRNA, messenger RNA ) whereupon translation follows. Translation means the translation of mRNA to amino The following relations were assumed (Alon, 2007):
Transcription : the production of mRNA
During the production of mRNA , several assumptions are taken into account. In order to transcribe a gene, a certain amount of inducer is required, assumed is that one molecule arabinose activates one gene, thus N =1 (Khlebnikov et al., 2000). Since we inserted a high copy vector, there are several copies of the AraC gene present, which was assumed to be 100 AraC genes (=N_cAraC). Per transcription, a RNA-polymerase performs the transcription at a certain speed Rtrans = 80 nt/s (Bremer et al., 1996) and assumed is one active RNA polymerase per gene (=nPolyAraC). Given these assumptions, the maximum produced mRNA for AraC could be calculated by:</br>
β_mRNAmax_AraC= R_trans/756*N_cAraC*nPolyAraC*10E-9
The change in the maximum produced mRNA of Arac is directly related to the inducer concentration, assuming the Hill equation rate (Alon, 2007), where K_araC is the activation coefficient (=C_(arabinose_out )) and N = 1 as described above.
β_(mRNA_AraC )= β_(mRNAmax_AraC )*(C_arabinose_in)/(〖K_AraC〗^N+〖C_arabinose_in〗^N )
Since mRNA is rather unstable, it will degrade with a factor α_(mRNA_AraC ). α_(mRNA_AraC ) = log(2) / THalf life time mRNA, with Thalf life time mRNA= 4 min (Taniguchi Y. et al, 2010). Therefore, the rate of change (per iteration) in mRNA of AraC is described as:
dC_(mRNA_AraC)= β_(mRNA_AraC )- α_(mRNA_AraC )*C_(mRNA_AraC )
Translation: the production of the protein, mRNA to protein
Given the calculated amount mRNA, the related amount of produced protein can be calculated, based on the same principle. Per strand mRNA several translation will be performed, pAraC = 10 (Alon, 2007). At steady state, a constant amount of mRNA will be produced and degraded, meaning C_(mRNA_AraC ) is constant if this is equal to β_(mRNA_AraC )/(α_(mRNA_AraC ) ). Multiplying these two factors, will lead to the concentration of ArAC protein. However, the AraC protein will also partly degrade, leading to the following equation to describe the production rate of Arac protein (Alon, 2007):
dc_AraC =p_AraC* β_(mRNA_AraC )/(α_(mRNA_AraC ) )–α_(p_AraC )*C_AraC
The α_(p_AraC ) is calculated by log(2)/ THalf time AraC, with THalf time ArAC = 2 min (Kolodubretz et al., 1981). The production of Mfp-5 is assumed to be similar in process, only varying the half life time of the Mfp-5 protein, which is 10 min (Haemers, 2003)
Transport of Mfp-5
Mfp5 is transported via an active mechanism. Because no kinetic mechanisms for the transport were available, the transport was simplified to a diffusion mechanism over the two membranes. The mechanism was as described in the transport of the inducer arabinose leading to the following equations (Fick’s Law):
Transport over inner membrane:
The rate of diffusion through the inner membrane is given by:
v_(Mfp5_inner )= -Diff.coef_(Mfp5_inner)*(((C_(p_(Mfp5_peri ) )- C_(〖p_Mfp5〗_in )))⁄V_peri )/(x_(m_in )*10E-5)
Assuming Mfp5 to be a small molecule, the diffusion coefficient is assumed to be 1E-12 µm2/s (alon, 2007). Since the cell is assumed to have a spherical shape, one could calculate the volume of the periplasm and the volume of the outer membrane, if the volume of the cell as well as the diameters of the membranes and periplasm are known. The volume of the cell is 1 µm3 (Kubitschek et al., 1986), the diameter of the inner membrane is 4 µm and the diameter of the outer membrane is assumed 8 µm (Mitra et al., 2004)(Graham et al., 1991)(Abramson et al., 2003). The concentration in the periplasm can be calculated as follows:
C_(Mfp5_periplasm )= v_(Mfp5_inner )*A_(innermembrane_periplasm)/V_periplasm
Transport over outer membrane:
Assuming the given values above, the rate of diffusion through the outer membrane is given by:
v_(Mfp5_outer)= -Diff.coef_(Mfp5_outer)*(((C_(p_(Mfp5_out ) )- C_(〖p_Mfp5〗_peri )))⁄V_(mem_out ) )/(x_(m_out )*10E-5
Whereupon the concentration Mfp-5 integrated in the outer membrane can be calculated as follows:
C_(Mfp5_periplasm )= v_(Mfp5_inner )*A_(periplasm_outer)/V_(outer_membrane )
The arabinose concentration outside the cell was 55 E-5 mol/L, a relatively high concentration, which is expected to cause a high production rate of the protein. (Kleinschmidt et al. (1996)) The maximal produced mfp-5 was produced after 750s. A maximal mfp-5 concentration of 0.038 mmol/L was determined.
Retrieved from "http://2011.igem.org/Team:TU-Delft/Project/Modelling"
 "
"