Team:British Columbia/Model1
From 2011.igem.org
| Line 7: | Line 7: | ||
</html> | </html> | ||
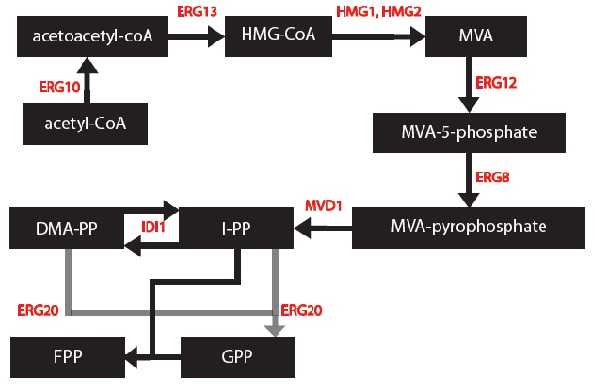
| - | First, a series of block diagrams to model the biochemical pathways were created. To illustrate, I started with the mevalonate pathway (Ignea et al. 2011) and simplified the pathway to only | + | First, a series of block diagrams to model the biochemical pathways were created. To illustrate, I started with the mevalonate pathway (Ignea et al. 2011) and simplified the pathway to only enzymes associated with our project – IDI1, HMG2 and ERG20. Since each yeast cell contained a different monoterpene synthase gene, the end of each biochemical pathway was modified accordingly to produce to correct monoterpenes. |
| - | + | I created differential equations based on the simplified biochemical pathways and chemical reactions. Dr. Eric Lagally referred me to 2 sources to help me make this conversion: “Writing Differential Equations” (Bourne 2010) and “Chapter 6- Transport and Kinetics” (Jakubowski 2011). The differential equations I made were based on using first order Michelson-menten kinetics. At this point, many constants and concentrations must be known to solve the differential equations. In particular, there is an enzyme database “BRENDA” which contains some of the values – kcat and km (Scheer 2011). Our project is based on research up until 2011 so some variables have yet to be experimentally determined. These differential equations will be solved in MATLAB and plots of concentration of monterpene as a function of substrate or time will be created. | |
| - | [[File:MODEL_1_-_Mevalonate_Pathway.jpg | frame | center | The Mevalonate Pathway as found in yeast | + | [[File:MODEL_1_-_Mevalonate_Pathway.jpg | frame | center | The Mevalonate Pathway as found in yeast. ]] |
| - | + | Our team wants to mass produce monoterpenes so we... | |
1) Replace HMG2 with the mutant variant K6R-hmg2, which is stabilized against protein degration (Gardner RG, Hampton RY: A 'distributed degron' allows regulated entry into the ER degradation pathway. Embo J 1999, 18: 5994-6004.) | 1) Replace HMG2 with the mutant variant K6R-hmg2, which is stabilized against protein degration (Gardner RG, Hampton RY: A 'distributed degron' allows regulated entry into the ER degradation pathway. Embo J 1999, 18: 5994-6004.) | ||
| Line 21: | Line 21: | ||
3) Introduce a gene which encodes for a synthase to use GPP to form monoterpenes. We chose 5 different synthases that each produces different monoterpenes in different proportions (Transcriptome mining, functional characterization, and phylogeny of a large terpene synthase gene family in spruce). | 3) Introduce a gene which encodes for a synthase to use GPP to form monoterpenes. We chose 5 different synthases that each produces different monoterpenes in different proportions (Transcriptome mining, functional characterization, and phylogeny of a large terpene synthase gene family in spruce). | ||
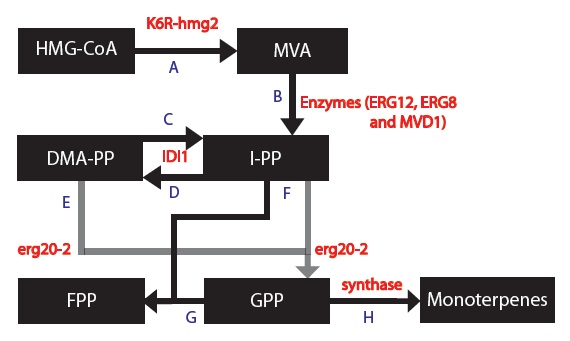
| + | Next, we created a modified and simplified model for the Mevalonate Pathway: | ||
| - | + | [[File:MODEL_1_-_Simplified_Model_Final.jpg | frame | center | Simplified model of the mevalonate pathway with the K6R-hmg2 and erg20-2 genes.]] | |
| - | + | ||
| - | [[File:MODEL_1_-_Simplified_Model_Final.jpg | frame | center | | + | |
<html><!-- Codes by Quackit.com --> | <html><!-- Codes by Quackit.com --> | ||
| Line 41: | Line 40: | ||
1) The enzymes ERG12, ERG8 and MVD1 are NOT RATE LIMITING; therefore, we chose not to include them in our simplified model. However, these enzymes are accounted for in our simulations. | 1) The enzymes ERG12, ERG8 and MVD1 are NOT RATE LIMITING; therefore, we chose not to include them in our simplified model. However, these enzymes are accounted for in our simulations. | ||
| - | 2) The RATE LIMITING STEP | + | 2) The RATE LIMITING STEP at the <html><a href="http://www.yeastgenome.org/cgi-bin/locus.fpl?locus=hmg2">HMG2</a></html> enzyme. |
| - | Next, we are using 5 different synthases which | + | Next, we are using 5 different synthases for which tests have been performed in vitro: |
Synthase PgTPS-Pin2 catalyzes GPP into producing 70.5% β-pinene and 29% α-pinene + other monoterpens in negligible amounts. | Synthase PgTPS-Pin2 catalyzes GPP into producing 70.5% β-pinene and 29% α-pinene + other monoterpens in negligible amounts. | ||
| Line 55: | Line 54: | ||
Synthase PsTPS-Pin catalyzes GPP into producing 83.4% α-pinene and 12.6% β-pinene + other monoterpens in negligible amounts. | Synthase PsTPS-Pin catalyzes GPP into producing 83.4% α-pinene and 12.6% β-pinene + other monoterpens in negligible amounts. | ||
| - | Source: | + | Source: Transcriptome mining, functional characterization, and phylogeny of large terpene synthase gene family in spruce (Picea spp.) |
| - | + | ||
I made a list of important common chemical reactions after developing this simplified version of the biochemical pathway: | I made a list of important common chemical reactions after developing this simplified version of the biochemical pathway: | ||
| Line 64: | Line 62: | ||
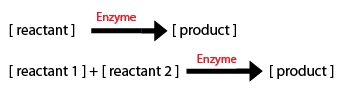
Now, I needed to model these chemical equations as a series of differential equations. As an engineer, I don't have a biochemistry background so this problem was new for me. This <html><a href="http://www.boomer.org/c/p3/c02/c0207.html">website</a></html> provided the basics to get started. 2 things to take into account are: | Now, I needed to model these chemical equations as a series of differential equations. As an engineer, I don't have a biochemistry background so this problem was new for me. This <html><a href="http://www.boomer.org/c/p3/c02/c0207.html">website</a></html> provided the basics to get started. 2 things to take into account are: | ||
| + | |||
1) The direction of the arrow: | 1) The direction of the arrow: | ||
-if the arrow goes into a component, the equation segment is positive | -if the arrow goes into a component, the equation segment is positive | ||
| Line 72: | Line 71: | ||
-if the rate process i first order, multiply the rate constant by the initial substrate concentration | -if the rate process i first order, multiply the rate constant by the initial substrate concentration | ||
-for a Michaelis-Menten process, include the amount or concentration of the component at the tail of the arrow (call it X1 for example) and you will get: d(X1)/dt = (-Vm*X1)/(Km+X1) | -for a Michaelis-Menten process, include the amount or concentration of the component at the tail of the arrow (call it X1 for example) and you will get: d(X1)/dt = (-Vm*X1)/(Km+X1) | ||
| - | |||
| - | |||
Most of the equations fall under the main 2 types of Michaelis–Menten equations: | Most of the equations fall under the main 2 types of Michaelis–Menten equations: | ||
| Line 84: | Line 81: | ||
2) S >> Eo | 2) S >> Eo | ||
| - | + | The second type of Michaelis-Menten kinetic equation applies to cases where I have 2 substrates combining into 1 product via a condensation reaction; DMA-PP and I-PP are condensed to generate geranyl diphosphate (GPP, C10), which is further converted with IPP into ferensyl diphosphate (FPP, C15), with prenyl transferase such as FPP synthase (Pathway engineering for functional isoprenoids.). | |
| - | + | Below is the 2 step reaction which shows the catalyzation via FPP synthase, | |
[[File:How_FPP_is_made.jpg | frame | center | Mechanism to produce FPP from I-PP and DMA-PP. (The role of ERG20 gene (encoding yeast farnesyl diphosphate synthase) mutated in long dolichol formation. Molecular modeling of FPP synthase)]] | [[File:How_FPP_is_made.jpg | frame | center | Mechanism to produce FPP from I-PP and DMA-PP. (The role of ERG20 gene (encoding yeast farnesyl diphosphate synthase) mutated in long dolichol formation. Molecular modeling of FPP synthase)]] | ||
| Line 94: | Line 91: | ||
where [S1] = concentration of substrate 1, [S2] = concentration of substrate 2. They have an associated kinetic value. Vmax = kcat*[E] where [E] = the concentration of enzyme. | where [S1] = concentration of substrate 1, [S2] = concentration of substrate 2. They have an associated kinetic value. Vmax = kcat*[E] where [E] = the concentration of enzyme. | ||
| - | The final thing I needed to consider before writing out the differential equations | + | The final thing I needed to consider before writing out the differential equations was how to use data indicating what percentage of monoterpenes were produced. These final steps also took the form of the Michaelis-Menten equations but I modified them by multiplying each by the fraction of product produced. For example, please look at equations 10 and 12 in the differential equations below to see fraction of products are produced for the PgTPS-Pin2 synthase. |
| - | + | ||
| - | + | ||
These are the differential equations that are common to each biochemical pathway: | These are the differential equations that are common to each biochemical pathway: | ||
[[File:Common_DE.jpg | frame | center | Differential equations common in all products. ]] | [[File:Common_DE.jpg | frame | center | Differential equations common in all products. ]] | ||
| - | |||
| - | |||
<html><!-- Codes by Quackit.com --> | <html><!-- Codes by Quackit.com --> | ||
Revision as of 06:03, 25 September 2011

MODEL 1: Secretion and Production of Monoterpenes in Yeast
OBJECTIVE: To create a model to assay the production of monoterpenes in our genetically engineered yeast cells given that they contain the metabolic genes IDI1, K6R-hmg2, erg20-2 and a monoterpene synthase. Model Creator: Gurpal Bisra
First, a series of block diagrams to model the biochemical pathways were created. To illustrate, I started with the mevalonate pathway (Ignea et al. 2011) and simplified the pathway to only enzymes associated with our project – IDI1, HMG2 and ERG20. Since each yeast cell contained a different monoterpene synthase gene, the end of each biochemical pathway was modified accordingly to produce to correct monoterpenes.
I created differential equations based on the simplified biochemical pathways and chemical reactions. Dr. Eric Lagally referred me to 2 sources to help me make this conversion: “Writing Differential Equations” (Bourne 2010) and “Chapter 6- Transport and Kinetics” (Jakubowski 2011). The differential equations I made were based on using first order Michelson-menten kinetics. At this point, many constants and concentrations must be known to solve the differential equations. In particular, there is an enzyme database “BRENDA” which contains some of the values – kcat and km (Scheer 2011). Our project is based on research up until 2011 so some variables have yet to be experimentally determined. These differential equations will be solved in MATLAB and plots of concentration of monterpene as a function of substrate or time will be created.
Our team wants to mass produce monoterpenes so we...
1) Replace HMG2 with the mutant variant K6R-hmg2, which is stabilized against protein degration (Gardner RG, Hampton RY: A 'distributed degron' allows regulated entry into the ER degradation pathway. Embo J 1999, 18: 5994-6004.)
2) Replace ERG20 with the mutant variant K197E erg20-2, which produces "25% FPP and 75% GPP instead of 75% FPP and 25% GPP" as compared to the wildtype ERG20 gene (Monoterpenoid biosynthesis in Saccharomyces cerevisiae.). We want more GPP than FPP because our goal is to produce monoterpenes and not diterpenoids (Pathway engineering for functional isoprenoids.).
3) Introduce a gene which encodes for a synthase to use GPP to form monoterpenes. We chose 5 different synthases that each produces different monoterpenes in different proportions (Transcriptome mining, functional characterization, and phylogeny of a large terpene synthase gene family in spruce).
Next, we created a modified and simplified model for the Mevalonate Pathway:
At this point, it is important to note 2 things: 1) The enzymes ERG12, ERG8 and MVD1 are NOT RATE LIMITING; therefore, we chose not to include them in our simplified model. However, these enzymes are accounted for in our simulations.
2) The RATE LIMITING STEP at the HMG2 enzyme.
Next, we are using 5 different synthases for which tests have been performed in vitro:
Synthase PgTPS-Pin2 catalyzes GPP into producing 70.5% β-pinene and 29% α-pinene + other monoterpens in negligible amounts.
Synthase PsTPS-Car1 catalyzes GPP into producing 66.4% 3-carene and 2.7% α-pinene + other monoterpens in negligible amounts.
Synthase PgxeTPS-Cin catalyzes GPP into producing 65.6% 1,8 cineole, 3.0% α-pinene and 2.6% β-pinene + other monoterpens in negligible amounts.
Synthase PgTPS-Cin catalyzes GPP into producing 81.1% 1,8 cineole, 1.9% α-pinene and 1.9% β-pinene + other monoterpens in negligible amounts.
Synthase PsTPS-Pin catalyzes GPP into producing 83.4% α-pinene and 12.6% β-pinene + other monoterpens in negligible amounts.
Source: Transcriptome mining, functional characterization, and phylogeny of large terpene synthase gene family in spruce (Picea spp.)
I made a list of important common chemical reactions after developing this simplified version of the biochemical pathway:
Since each synthase gene combines with GPP to produce different monoterpenes, some chemical reactions will be specific to a certain synthase.
Now, I needed to model these chemical equations as a series of differential equations. As an engineer, I don't have a biochemistry background so this problem was new for me. This website provided the basics to get started. 2 things to take into account are:
1) The direction of the arrow: -if the arrow goes into a component, the equation segment is positive -if the arrow leaves a component, the equation segment is negative
2) Types of Rate Processes -if the rate process is zeroth order, just enter the rate constant -if the rate process i first order, multiply the rate constant by the initial substrate concentration -for a Michaelis-Menten process, include the amount or concentration of the component at the tail of the arrow (call it X1 for example) and you will get: d(X1)/dt = (-Vm*X1)/(Km+X1)
Most of the equations fall under the main 2 types of Michaelis–Menten equations:
For the first type of reaction, I had to make 2 assumptions:
1) At steady state, [ES] does not change with time, therefore it's derivative with time is = 0. Therefore, k1[E][S] = (k2+k3)[ES]
2) S >> Eo
The second type of Michaelis-Menten kinetic equation applies to cases where I have 2 substrates combining into 1 product via a condensation reaction; DMA-PP and I-PP are condensed to generate geranyl diphosphate (GPP, C10), which is further converted with IPP into ferensyl diphosphate (FPP, C15), with prenyl transferase such as FPP synthase (Pathway engineering for functional isoprenoids.).
Below is the 2 step reaction which shows the catalyzation via FPP synthase,
To model these types of reactions, I found an expression for the reaction velocity to be: v = d(X)/dt = (Vmax)/( (kms1/[S1]) + (kms2/[S2]) + 1 ) where [S1] = concentration of substrate 1, [S2] = concentration of substrate 2. They have an associated kinetic value. Vmax = kcat*[E] where [E] = the concentration of enzyme.
The final thing I needed to consider before writing out the differential equations was how to use data indicating what percentage of monoterpenes were produced. These final steps also took the form of the Michaelis-Menten equations but I modified them by multiplying each by the fraction of product produced. For example, please look at equations 10 and 12 in the differential equations below to see fraction of products are produced for the PgTPS-Pin2 synthase.
These are the differential equations that are common to each biochemical pathway:
The differential equations specific to the PsTPS-Pin synthase, PgTPS-Pin2 synthase, PsTPS-Car1 synthase, PgxeTPS-Cin synthase, PgTPS-Cin synthase.
 "
"