Results
Contents |
Parts assembly
Characterization of basic modules
Characterization of promoters pTet and pLux
Inducible and constitutive promoters were assembled upstream of different coding sequences containing an RBS from the Community collection.
The assembled RBSs are:
| BioBrick code | Declared efficiency |
| BBa_B0030 | 0,6 |
| BBa_B0031 | 0,07 |
| BBa_B0032 | 0,3 |
| BBa_B0034 | 1 |
For an inducible device, the RBS variation has the purpose to stretch the induction curve, thus modulating its PoPs-OUT range.
The complex RBS-promoter acts as a whole regulatory element and determines the amount of translated protein. RBSs have been reported to have an un-modular behavior, since the translational efficiency is not independent on the coding sequences, but variates as an effect of different mRNA structure stability [Salis et al., Nat Biotec, 2009]. It is not possible to separate the effects of the sole promoter and of the sole RBS on the total amount/activity of gene product (in this case study, mRFP).
For this reason, every combination 'Promoter+RBS' was studied as a different regulatory element. Regulatory elements were characterized using mRFP reporter protein for different RBSs in terms of Synthesis rate per Cell (Scell) and R.P.U.s (Relative Promoter Units) as explained in measurements section.
Operative parameters of the promoter are derived from the estimated Hill equations obtained by nonlinear least squares fitting (lsqnonlin Matlab routine) of the Hill function expressed in RPUs:
- RPUmax is equal to the α and represents the maximum promoter activity
- RPUmin is equal to the α * δ represents the minimum promoter activity
- Switch point is computed as the abscissa of the inflection point of the Hill curve and it is representative of the position of linear region
- Linearity boundaries are determined as the intersection between the tangent line to the inflection point and the upper and lower horizontal boundaries of the Hill curve.
The estimated parameters for the Hill functions of pLux are summarized in the table below. For more details on parameter estimation, see the model section.
| RBS | αpLux [(AUr/min)/cell] | δpLux [-] | ηpLux [-] | kpLux [ng/ml] |
| BBa_B0030 | 438 [10] | 0.05 [>100] | 2 [47] | 1.88 [27] |
| BBa_B0031 | 9.8 [7] | 0.11 [57] | 1.2 [29] | 1.5 [26] |
| BBa_B0032 | 206 [3] | 0 [>>100] | 1.36 [10] | 1.87 [9] |
| BBa_B0034 | 1105 [6] | 0.02 [>100] | 1.33 [19] | 2.34 [18] |
The operative parameters are summarized in the table below:
| RBS | RPUmax | RPUmin | Switch point [nM] | Linear boundaries [MIN; MAX] [nM] |
| B0030 | 4.28 | 0.20 | 1.08 | [0.36; 3.27] |
| B0031 | 4.93 | 0.55 | 0.25 | [0.03; 2.30] |
| B0032 | 9.49 | 0.02 | 0.47 | [0.07; 3.07] |
| B0034 | 21.53 | 0.51 | 0.53 | [0.08; 3.77] |
The protocols for the characterization of pTet promoter are reported in the pTet measurement section.
Here we have characterized its transcriptional strength as a function of aTc induction (ng/ul) for different RBSs. Three different induction curves were obtained and are reported in figure:
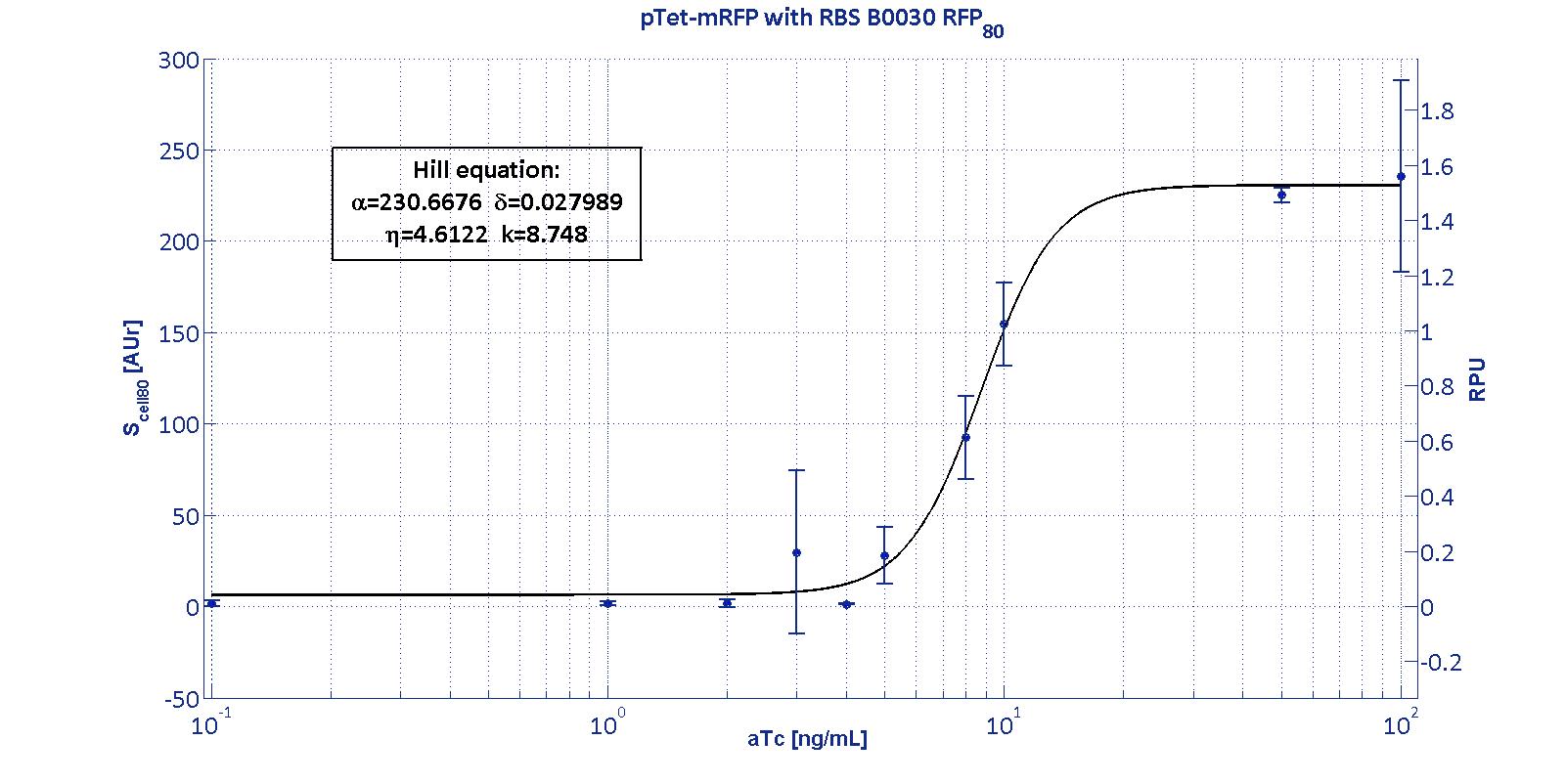
The estimated parameters of the Hill curves described in the figures are summarized in the table below:
| RBS | αpTet [(AUr/min)/cell] | δpTet [-] | ηpTet [-] | kpTet [nM] |
| BBa_B0030 | 230.67 [3.7] | 0.028 [91.61] | 4.61 [23.73] | 8.75 [4.16] |
| BBa_B0031 | ND | ND | ND | ND |
| BBa_B0032 | 55.77 [12] | 1.53E-11 [>>100] | 4.98 [57.62] | 7.26 [14.98] |
| BBa_B0034 | 120 [5.95] | 0.085 [40.6] | 24.85 [47.6] | 9 [5.43] |
The operative parameters are summarized in the table below:
| RBS | RPUmax | RPUmin | Switch point [ng/ml] | Linear boundaries [MIN; MAX] [ng/ml] |
| B0030 | 1.53 | ~0 | 7.95 | [4.66;11.99] |
| B0031 | ND | ND | ND | ND |
| B0032 | 3.16 | ~0 | 6.7 | [4.45;10.05] |
| B0034 | 2.73 | 0.23 | 8.96 | [8.27;9.71] |
Characterization of enzymes AiiA and LuxI
Characterization of the efficiency of RBSs from the community collection
Identification of bacterial growth parameters
The bacterial growth curve has been modelled as a logistic curve and is represented by the following equation:
dN/dt=N*μ*(Nmax-N)/Nmax
N(0)=n0
where μ represents the growth rate of the cells (E. coli MGZ1 in M9 supplemented medium) and Nmax represents the maximum number of cells in the well. For a detailed description of the parameters, see modelling section. For details on parameters identification, see identification section.
The growth curves in all the performed experiments are measured in O.D.600. Since the N species in the model is expressed in cell number, a conversion factor has been estimated. The conversion factor KO.D.toC.F.U. has been estimated as follows.
- Two cultures C1 and C2 (MGZ1 cells) were grown in 1ml M9 medium till saturation (ON liquid culture, 37°C, 220 rpm).
- Next morning, both C1 and C2 were diluted in M9 medium with a final volume of 1ml with the following dilution factors:
- 1:1
- 1:10
- 1:100
- 1:1000
- After 1 hour, O.D.600 was measured using TECAN microplate reader (don't forget to measure a M9 sample for blanking!)
NB: from now on, cultures must be placed in ice to stop cell growth. - At the same time, proper dilution of the cultures were plated on LB agar plates.
NB: All the dilutions are performed moving 100 μl of culture in previously ice-chilled 900 μl fresch M9. 100 μl of the final dilution are plated (It still represents a 1:10 dilution!) - Plates were grown overnight and next morning C.F.U. were counted.
- C.F.U. values were corrected by the dilution factor and a linear regression (N vs O.D.600) was performed in order to evaluate the conversion factor KO.D.toC.F.U..
- KO.D.toC.F.U. was used as conversion factor to multiply the O.D.600 value of saturation in the growth curves (~0,5).
The results are summarized in the table and in the figure below:
| Culture | O.D.600 TECAN | O.D.600 Spectrophotometer | C.F.U. | Dilution Factor (10^) | N |
| C1 | 0,367950002 | 0,758004416 | 990 | 5 | 990000000 |
| C1 | 0,044649998 | 0,091982322 | 141 | 6 | 1410000000 |
| C1 | 0,004799999 | 0,009888356 | 136 | 5 | 136000000 |
| C1 | 0,000549998 | 0,001133037 | 20 | 6 | 200000000 |
| C2 | 0,54840003 | 1,129744917 | 165 | 4 | 16500000 |
| C2 | 0,058200002 | 0,119896339 | 23 | 5 | 23000000 |
| C2 | 0,008700002 | 0,017922652 | 251 | 3 | 2510000 |
| C2 | 0,000100002 | 0,000206011 | 24 | 4 | 2400000 |

The estimation of μ parameter was performed by determining the slope of the logarithmic curve of O.D.600 in exponential phase. Exponential phase was determined by visual inspection as the linear phase of the logarithmic curve of O.D.600.
The estimated parameters are summarized in the table below:
| Nmax [cell number] | μ [min-1] |
| 1*109 | 0.004925 |
The reported value of μ corresponds to a doubling time of 142 minutes.
Estimation of the spontaneous degradation of HSL in M9 medium and in cultures at different pH values
In order to estimate the spontaneous degradation rate of HSL in M9 medium and in a culture of MGZ1 cells as a function of pH, two simple tests have been performed.
Two different M9 media were prepared, one with the nominal pH (7.0) and one with pH=6.0.
These media, now named respectively M9pH 7 and M9pH 6, were added with a known concentration of HSL (100 nM) and then incubated at 37°C, 220 rpm (NB: the media were not infected with any culture but the standard growth conditions were reproduced). The amount of HSL present in the medium was assayed through the BBa_T9002 biosensor at 4 time points:
- t=0 h;
- t=1 h;
- t=2 h;
- t=4 h;
- t=8 h;
The obtained time series of HSL amounts were processed to evaluate the time constant governing the dynamic of HSL degradation, supposing an exponential decay. The results are reported in the table below:
| t1/2* [h] | γHSL** [h-1] | |
| M9pH 6 | 32 | 0.022 |
| M9pH 7 | 8 | 0.087 |
The described experiment was repeated with a MGZ1 culture in order to evaluate the effect of culture on HSL stability. The estimated values are reported in the table below:
| t1/2* [h] | γHSL** [h-1] | |
| CulturepH 6 | ∞ | 0 |
| CulturepH 7 | 19 | 0.037 |
It is evident from the reported data that the spontaneous degradation of HSL is negligible when CTRL+E is implemented in MGZ1 cells grown in M9 medium with pH=6.0 and pH=7.0.
Thus in the simulations we set γHSL=0;
Characterization of BBa_T9002 biosensor
As described in the modelling section, BioBrick BBa_T9002 is an HSL biosensor, which provides a non linear relationship between HSL input and Scell output. More precisely, the characteristic sigmoidal curve requires synthetic parameters for its accurate identification. These are the minimum and maximum values, the swtich point (i.e., the curve inflection point), and the upper and lower boundaries of linearity. This biosensor revealed greatly reliable, providing measurement repeatability and minimal experimental noise. Referring to its activation formula, the calibration curve is shown below.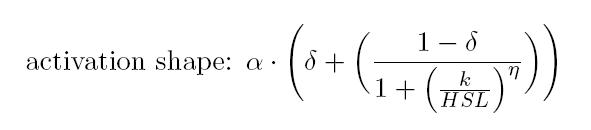
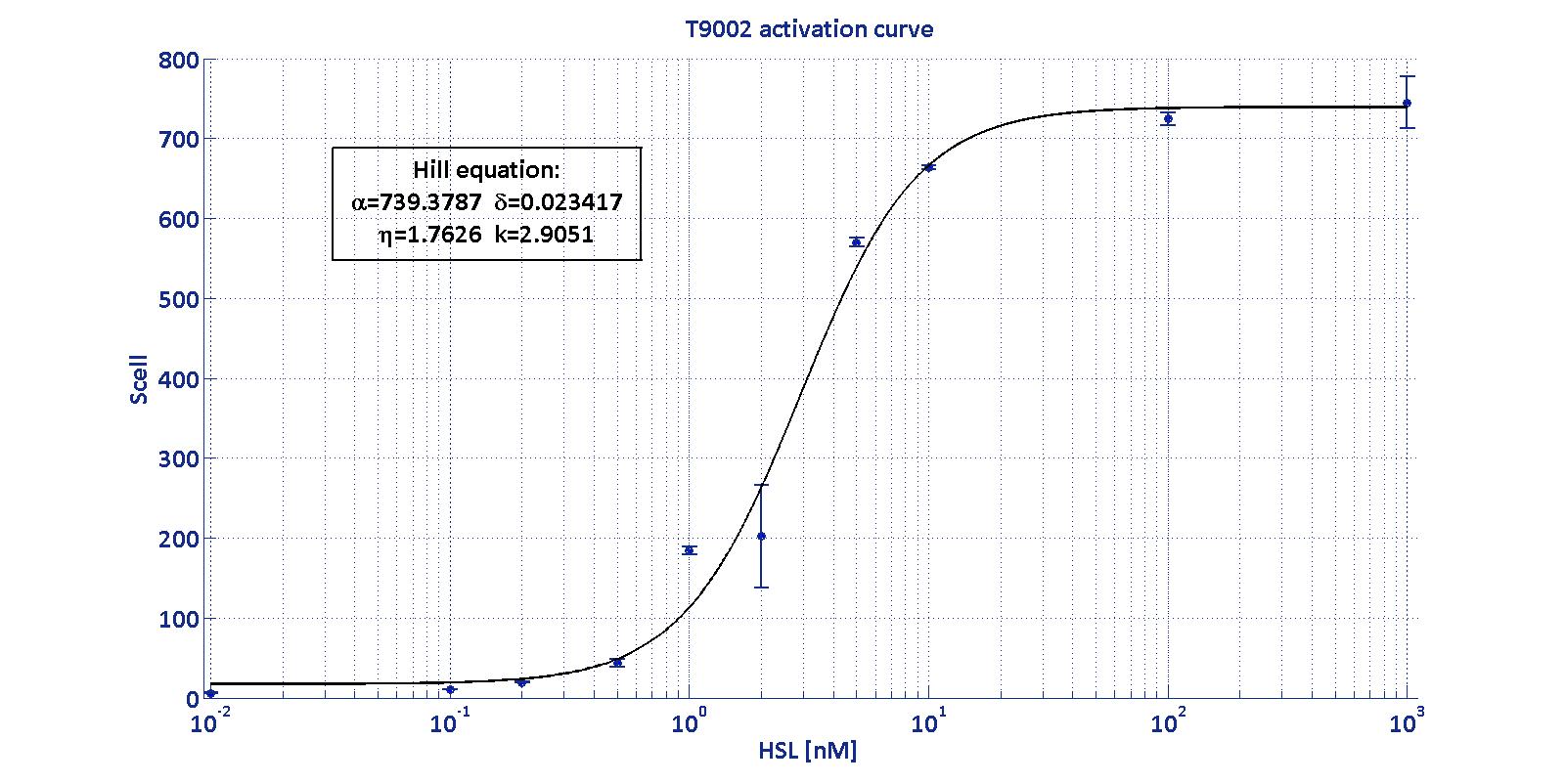
| Minimum [Scell] | Maximum [Scell] | Switch point [nM] | Lower boundary of linearity [nM] | Upper boundary of linearity [nM] |
| 17.31 | 739.4 | 1.39 | 0.38 | 5.07 |
In order to determine the threshold sensitivity of T9002 biosensor, experiments were performed with several HSL inductions minimally interspaced in the region of low detectability. Hypothesizing that the inducer is 1:20 diluted (as for all of our tests), the minimum detectable HSL concentration is 3 nM.
 "
"





