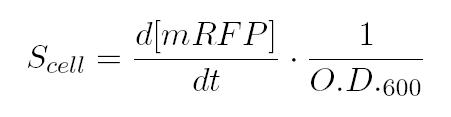Modelling
Contents |
Mathematical modelling: introduction
Mathematical modelling plays a central role in Synthetic Biology, due to its ability to serve as a crucial link between the concept and realization of a biological circuit: what we propose in this page is a mathematical modelling approach to the entire project, which has proven extremely useful before and after the "wet lab" activities.
Thus, immediately at the beginning, when there was little knowledge, a mathematical model based on a system of differential equations was derived and implemented using a set of reasonable values of model parameters, to validate the feasibility of the project. Once this became clear, starting from the characterization of each simple subpart created in the wet lab, some of the parameters of the mathematical model were estimated thanks to several ad-hoc experiments we performed within the iGEM project (others were derived from literature) and they were used to predict the final behaviour of the whole engineered closed-loop circuit. This approach is consistent with the typical one adopted for the analysis and synthesis of a biological circuit, as exemplified by Pasotti L et al. 2011.
After a brief overview on the importance of the mathematical modelling approach, we deeply analyze the system of equations, underlining the role and function of the parameters involved.
Experimental procedures for parameter estimation are discussed and simulations performed, using ODEs with MATLAB.
The importance of mathematical modelling
Mathematical modelling reveals fundamental in the challenge of understanding and engineering complex biological systems. Indeed, these are characterized by a high degree of interconnection among the single constituent parts, requiring a comprehensive analysis of their behavior through mathematical formalisms and computational tools.
- Simulation: mathematical models allow to analyse complex system dynamics and to reveal the relationships between the involved variables, starting from the knowledge of the single subparts behavior and from simple hypotheses of their interconnection. (Endler L et al. 2009)
- Knowledge elicitation: mathematical models summarize into a small set of parameters the results of several experiments (parameter identification), allowing a robust comparison among different experimental conditions and providing an efficient way to synthesize knowledge about biological processes. Then, through the simulation process, they make possible the re-usability of the knowledge coming from different experiments, engineering complex systems from the composition of its constituent subparts under appropriate experimental/environmental conditions (Braun D et al. 2005; Canton B et al 2008).
Equations for gene networks
Below is provided the system of equations of our mathematical model.
 |

Hypotheses of the model
|
HP1: in equation (2) only HSL is considered as inducer, instead of the complex LuxR-HSL.
This is motivated by the fact that our final device offers a constitutive LuxR production due to the upstream constitutive promoter Pλ. Assuming LuxR is abundant in the cytoplasm, we can understand this simplification of attributing pLux promoter induction only by HSL.
HP2: in system equation, LuxI and AiiA amounts are expressed per cell. For this reason, the whole equation (3), except for the term of intrinsic degradation of HSL, is multiplied by the number of cells N, due to the property of the lactone to diffuse freely inside/outside bacteria. HP3: as regards promoters pTet and pLux, we assume their strengths (measured in PoPs), due to a given concentration of inducer (aTc and HSL for Ptet and Plux respectively), to be independent from the gene downstream. In other words, in our hypothesis, if the mRFP coding region is substituted with a region coding for another gene (in our case, AiiA or LuxI), we would obtain the same synthesis rate: this is the reason why the strength of the complex promoter-RBS is expressed in Arbitrary Units [AUr]. HP4: considering the exponential growth, the enzymes AiiA and LuxI concentration is supposed to be constant, because their production is equally compensated by dilution. |
Equations (1) and (2)
Equations (1) and (2) have identical structure, differing only in the parameters involved. They represent the synthesis, degradation and dilution of both the enzymes in the circuit, LuxI and AiiA, respectively in the first and second equation: in each of them both transcription and translation processes have been condensed. The mathematical formulation is analogous to the one used by Pasotti L et al. 2011, Suppl. Inf., even if we do not take LuxR-HSL complex formation into account, as explained below.
These equations are composed of 2 parts:
- The first term describes, through Hill's equation, the synthesis rate of the protein of interest (either LuxI or AiiA) depending on the concentration of the inducer (anhydrotetracicline -aTc- or HSL respectively), responsible for the activation of the regulatory element composed of promoter and RBS. In the parameter table (see below), α refers to the maximum activation of the promoter, while δ stands for its leakage activity (this means that the promoter is slightly active even if there is no induction). In particular, in equation (1), the almost entire inhibition of pTet promoter is given by the constitutive production of TetR by our MGZ1 strain. In equation (2), pLux is almost inactive in the absence of the complex LuxR-HSL. Furthermore, in both equations k stands for the dissociation constant of the promoter from the inducer (respectively aTc and HSL in eq. 1 and 2), while η is the cooperativity constant.
- The second term in equations (1) and (2) is in turn composed of 2 parts. The former one (γ*LuxI or γ*AiiA respectively) describes, with an exponential decay, the degradation rate per cell of the protein. The latter (μ*(Nmax-N)/Nmax)*LuxI or μ*(Nmax-N)/Nmax)*AiiA, respectively) takes into account the dilution factor against cell growth which is related to the cell replication process.
Equation (3)
Here the kinetics of HSL is modeled, through enzymatic reactions either related to the production or the degradation of HSL. This equation is composed of 3 parts:
- The first term represents the production of HSL due to LuxI expression. We modeled this process with a saturation curve in which Vmax is the HSL maximum transcription rate, while kM,LuxI is LuxI dependent half-saturation constant.
- The second term represents the degradation of HSL due to the AiiA expression. Similarly to LuxI, kcat represents the maximum degradation per unit of HSL concentration, while kM,AiiA is the concentration at which AiiA dependent HSL degradation rate is (kcat*HSL)/2. The formalism is similar to that found in the Supplementary Information of Danino T et al 2010.
- The third term (γHSL*HSL) is similar to the corresponding ones present in the first two equations and describes the intrinsic protein degradation.
Equation (4)
Table of parameters and species
| Parameter & Species | Description | Measurement Unit | Value |
| αpTet | maximum transcription rate of pTet (dependent on RBSx efficiency) | [(AUr/min)/cell] | 230.67 (RBS30) ND (RBS31) 55.77 (RBS32) 120 (RBS34) |
| δpTet | leakage factor of promoter pTet basic activity | [-] | 0.028 (RBS30) ND (RBS31) 1.53E-11 (RBS32) 0.085 (RBS34) |
| ηpTet | Hill coefficient of pTet | [-] | 4.61 (RBS30) ND (RBS31) 4.98 (RBS32) 24.85 (RBS34) |
| kpTet | dissociation constant of aTc from pTet | [ng/ml] | 8.75 (RBS30) ND (RBS31) 7.26 (RBS32) 9 (RBS34) |
| αpLux | maximum transcription rate of pLux (dependent on RBSx efficiency) | [(AUr/min)/cell] | 438 (RBS30) 9.8 (RBS31) 206 (RBS32) 1105 (RBS34) |
| δpLux | leakage factor of promoter pLux basic activity | [-] | 0.05 (RBS30) 0.11 (RBS31) 0 (RBS32) 0.02 (RBS34) |
| ηpLux | Hill coefficient of pLux | [-] | 2 (RBS30) 1.2 (RBS31) 1.36 (RBS32) 1.33 (RBS34) |
| kpLux | dissociation constant of HSL from pLux | [nM] | 1.88 (RBS30) 1.5 (RBS31) 1.87 (RBS32) 2.34 (RBS34) |
| γLuxI | LuxI constant degradation | [1/min] | 0.0173 |
| γAiiA | AiiA constant degradation | [1/min] | 0.0173 |
| γHSL | HSL constant degradation | [1/min] | 0 (pH=6) |
| Vmax | maximum transcription rate of LuxI per cell | [nM/(min*cell)] | 3.56*10-9 |
| kM,LuxI | half-saturation constant of LuxI from HSL | [AUr/cell] | 6.87*103 |
| kcat | maximum number of enzymatic reactions catalyzed per minute | [1/(min*cell)] | ND |
| kM,AiiA | half-saturation constant of AiiA from HSL | [AUr/cell] | ND |
| Nmax | maximum number of bacteria per well | [cell] | 1*109 |
| μ | rate of bacteria growth | [1/min] | 0.004925 |
| LuxI | kinetics of LuxI enzyme | [AUr⁄cell] | - |
| AiiA | kinetics of AiiA enzyme | [AUr⁄cell] | - |
| HSL | kinetics of HSL | [nM] | - |
| N | number of cells | cell | - |
In order to better investigate the range of dynamics of each subpart, every promoter has been studied with 4 different RBSs, so as to develop more knowledge about the state variables in several configurations of RBS' efficiency (Salis HM et al. 2009). Hereafter, referring to the notation "RBSx" we mean, respectively, RBS30, RBS31, RBS32, RBS34.
Parameter CV
| Parameter & Species | BBa_B0030 | BBa_B0031 | BBa_B0032 | BBa_B0034 |
| αpTet | 3.7 | ND | 12 | 5.94 |
| δpTet | 91.61 | >>100 | >100 | 40.59 |
| ηpTet | 23.72 | >>100 | 57.62 | 47.6 |
| kpTet | 4.16 | >>100 | 14.99 | 5.43 |
| αpLux | 10.14 | 7.13 | 2.78 | 5.8 |
| δpLux | 179.7 | 57.04 | 1317.7 | 187.2 |
| ηpLux | 47.73 | 29.13 | 9.75 | 19.3 |
| kpLux | 27.5 | 25.81 | 8.46 | 17.86 |
Parameter estimation
Promoter (PTet & pLux)
 |
 |
These are the first parts tested, with the target of learning more about pTet and pLux promoters. In particular, as previously explained in NOTE, for each promoter, we tested four different combinations of promoter-RBS, providing us a set of fundamental building blocks for the subsequent assebly of the closed-loop circuit.
As shown in the figure below, we considered a range of inductions and we monitored, in time, absorbance (O.D. stands for "optical density") and fluorescence; the two vertical segments for each graph highlight the exponential phase of bacterial growth. Scell (namely, synthesis rate per cell) can be derived as a function of inducer concentration, thereby providing the desired input-output relation (inducer concentration versus promoter+RBS activity), which was modelled as a Hill curve:
However, also Relative Promoter Unit (RPU, Kelly JR et al. 2009) has been calculated as a ratio of Scell of promoter of interest and the Scell of BBa_J23101 (reference to HP3).As shown in the figure, α, as already mentioned, represents the protein maximum synthesis rate, which is reached, in accordance with Hill equation, when the inducer concentration tends to infinite, and, more practically, when the inducer concentration is sufficiently higher than the dissociation constant. Meanwhile the product α*δ stands for the leakage activity (at no induction), liable for protein production (LuxI and AiiA respectively) even in the absence of inducer.
The paramenter η is the Hill's cooperativity constant and it affects the ripidity of transition from the lower and upper boundary of the curve relating Scell to the inducer concentration.
Lastly, k stands for the semi-saturation constant and, in case of η=1, it indicates the concentration of substrate at which half the synthesis rate is achieved.
T9002 introduction
LuxI and AiiA tests have been always performed exploiting the well-characterized BioBrick BBa_T9002, by which it's possible to quantify exactly the concentration of HSL.

This is a biosensor which receives HSL concentration as input and returns GFP intensity (more precisely Scell) as output. (Canton et al. 2008). According to this, it is necessary to understand the input-output relationship: so, a T9002 "calibration" curve is plotted for each test performed.
AiiA & LuxI
This paragraph explains how parameters of equation (3) are estimated. The target is to learn the AiiA degradation and LuxI production mechanisms in addiction to HSL intrinsic degradation, in order to estimate Vmax, KM,LuxI, kcat, KM,AiiA and γHSL parameters. We adopt tests composed of two steps. In the first one, the following BioBrick parts are used:
 |
 |
Based on our HP3 and HP4, we are able to determine AiiA and LuxI concentrations, provided we have yet characterized pTet-RBSx contructs. In particular, referring to HP4, in exponential growth the equilibrium of the enzymes is conserved. Due to a known induction of aTc, the steady-state level per cell can be calculated:
Then, as a second step, we monitor in separate experiments HSL synthesis and degradation caused by the activities of the enzymes. In other words, our idea is to control the degradation of HSL versus time. ATc activates pTet and, later, a certain concentration of HSL is introduced. Then, at fixed times, O.D.600 and HSL concentration are monitored using Tecan and T9002 biosensor.
For example for LuxI dependent HSL production, we have:
Therefore, considering for a determined promoter-RBSx couple, several induction of aTc and, for each of them, several samples of HSL concentration during time, parameters Vmax, kM,LuxI, kcat and kM,AiiA can be estimated, through numerous iterations of an algorithm implemented in MATLAB.
N
Degradation rates
Simulations
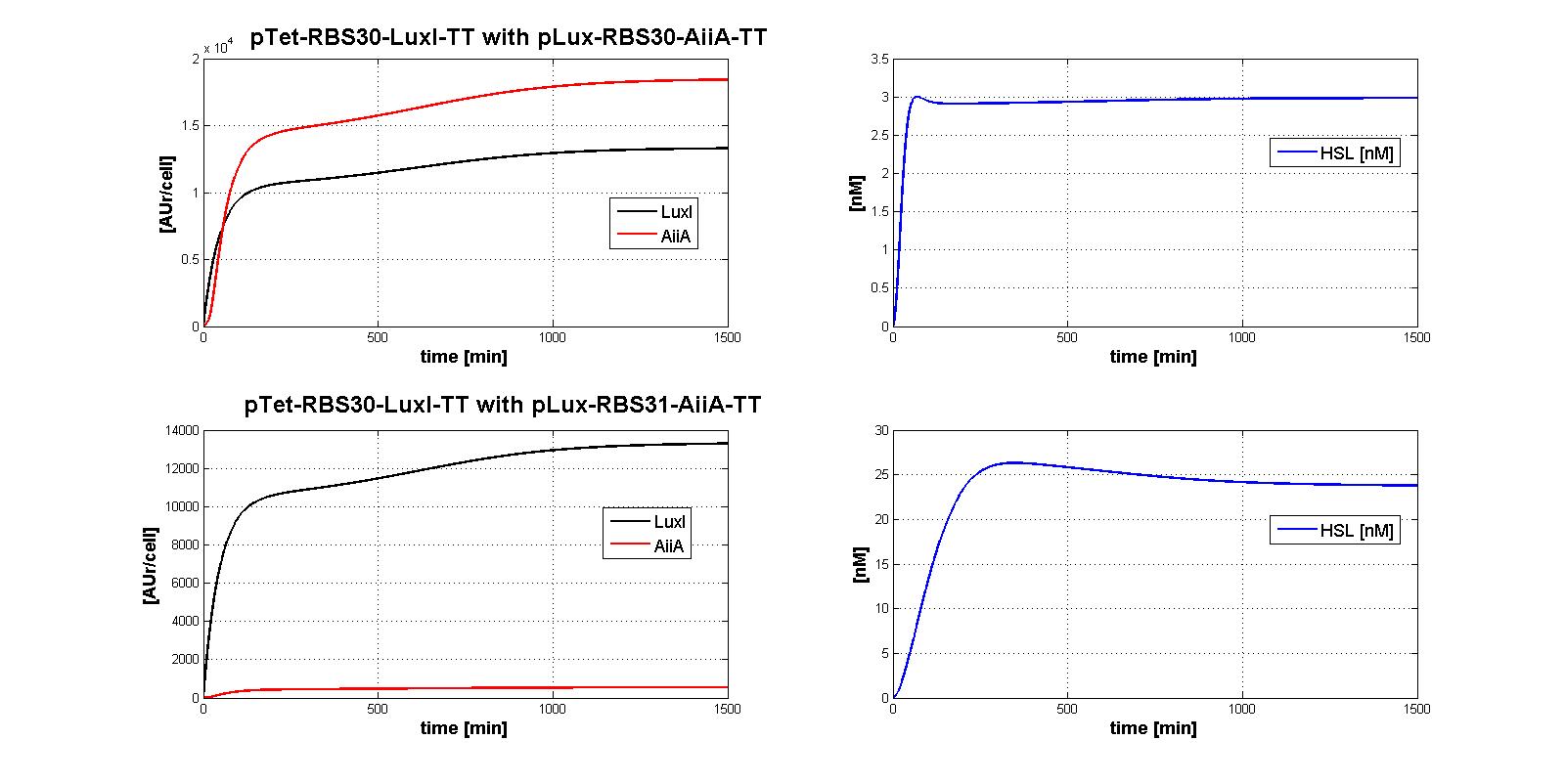
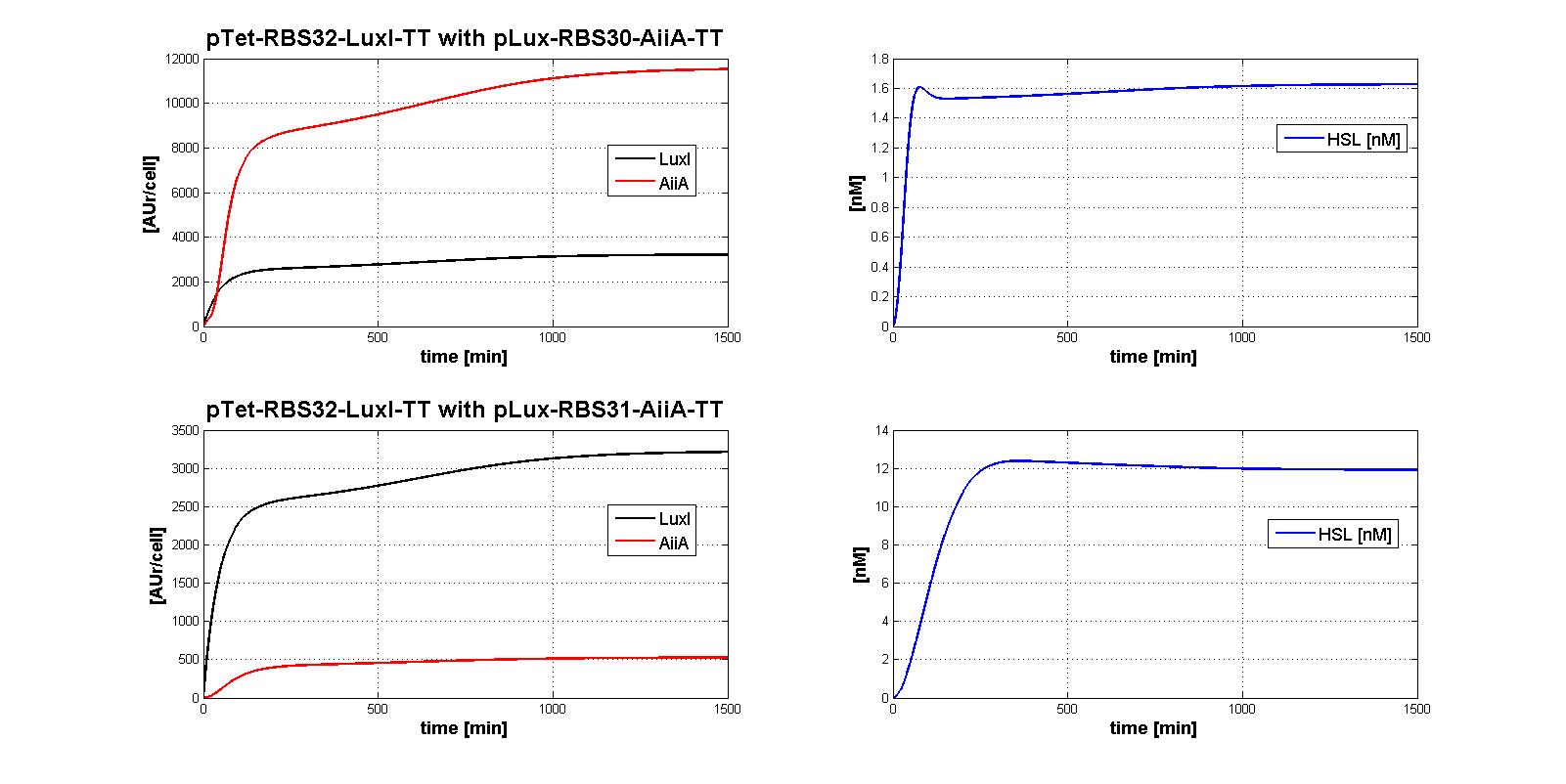
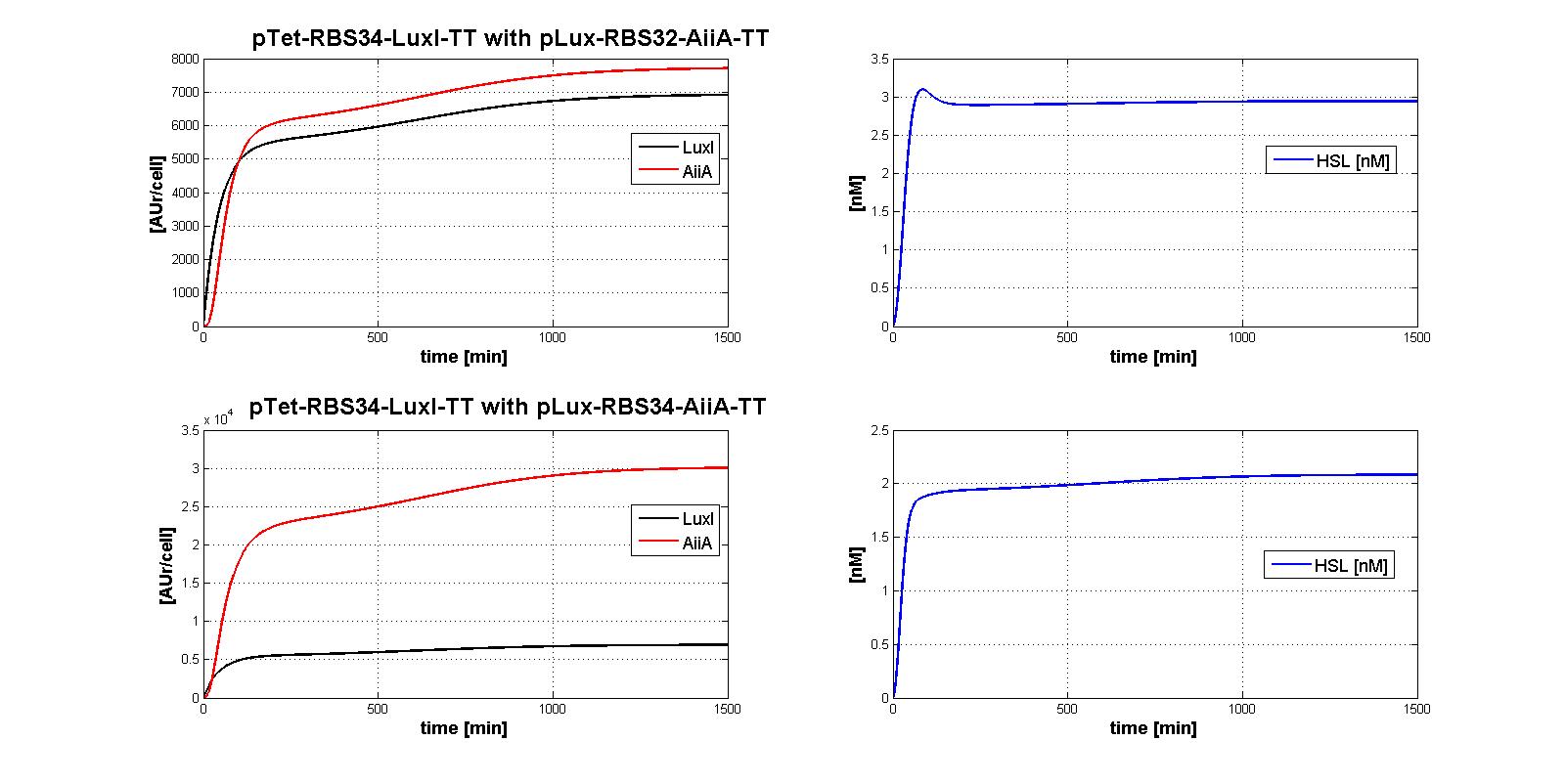
All the combinations of pTet-RBSx and pLux-RBSx were simulated using ODEs', in case of aTc=100 ng/ml. As explained in AiiA gene - BBa_C0060 section, parameters kcat and kM,AiiA were difficult to estimate from the collected data.
Here simulations are performed assuming reasonable values for kcat and kM,AiiA (1*10-9 [1/(min*cell)] and kM,AiiA=5000 [AUr/cell], respectively).
Obviously, increasing the kcat value, the HSL steady-state concentration decreases. Nevertheless, if you consider 100-fold variation of kcat value, the steady state of HSL is in the range about [0.08-0.7] nM.
Sensitivity Analysis of the steady state of enzyme expression in exponential phase
In this paragraph we investigate the theoretical behaviour of our circuit in the cell culture exponential growth phase. According to this, we first derive, under feasible hypotheses, the steady state condition for the enzymes and HSL concentration in that phase. Then we perform a sensitivity analysis relating the output of our system (HSL) to input (aTc) and system parameters.
Steady state of enzyme expression
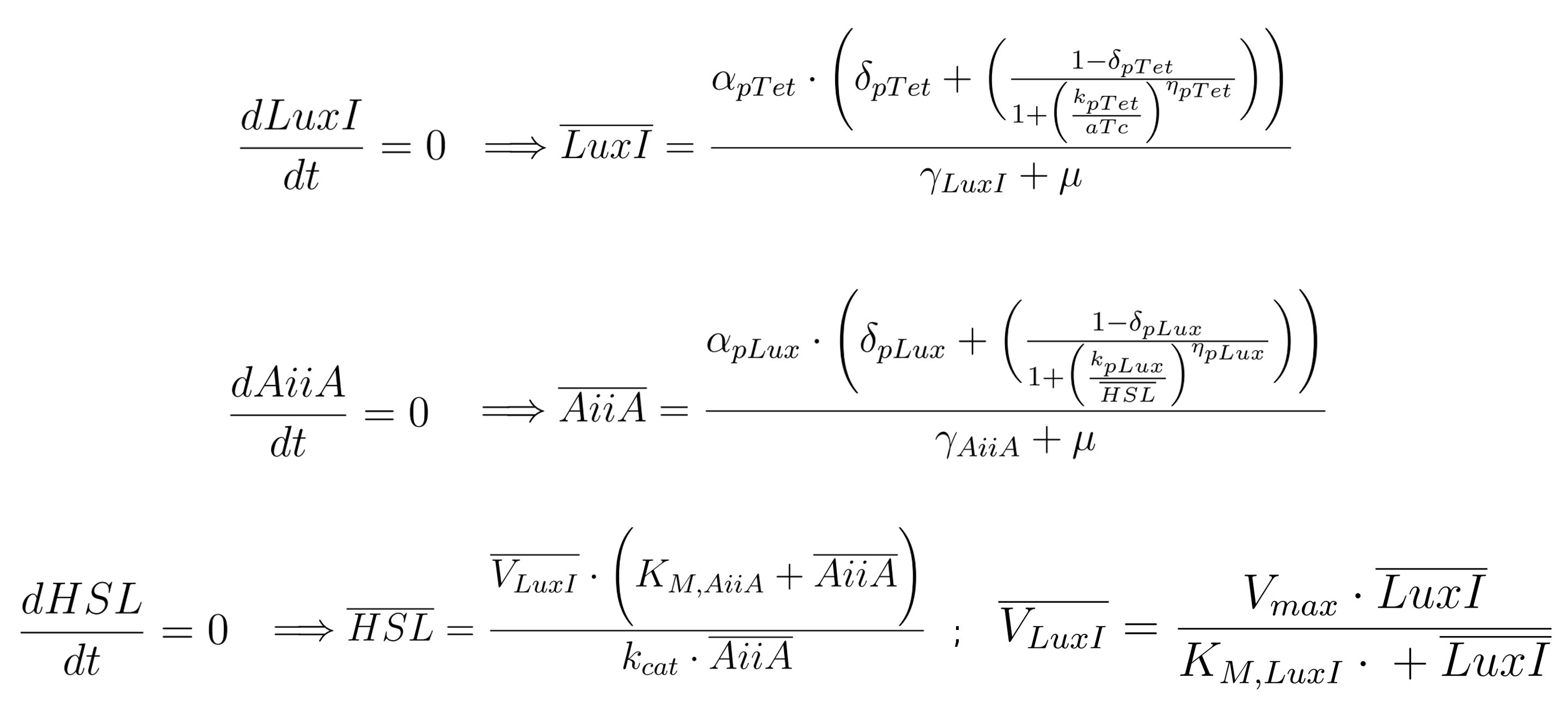
Based on HP4, we can formulate the steady state expressions during the exponential growth phase. Adding other considerations about the involved processes, it is possible to further simplify the steady state equations. In particular, one concern relates to the number of cells N (in the order of 10^7), which is far lower than Nmax (10^9). The other pertains to γ*HSL parameter, which can be neglected compared to the other two terms of the third equation, considering pH=6. Based on this assumptions, equation (4) of the system becomes dN/dt=μN. Moreover, from equation (3), after having removed the third term, we can simplify the N parameter, since it is common to the remaining two terms. On a biological point of view, this implies that AiiA, LuxI and HSL undergo only minor changes through time, thereby allowing to derive their steady state expressions:
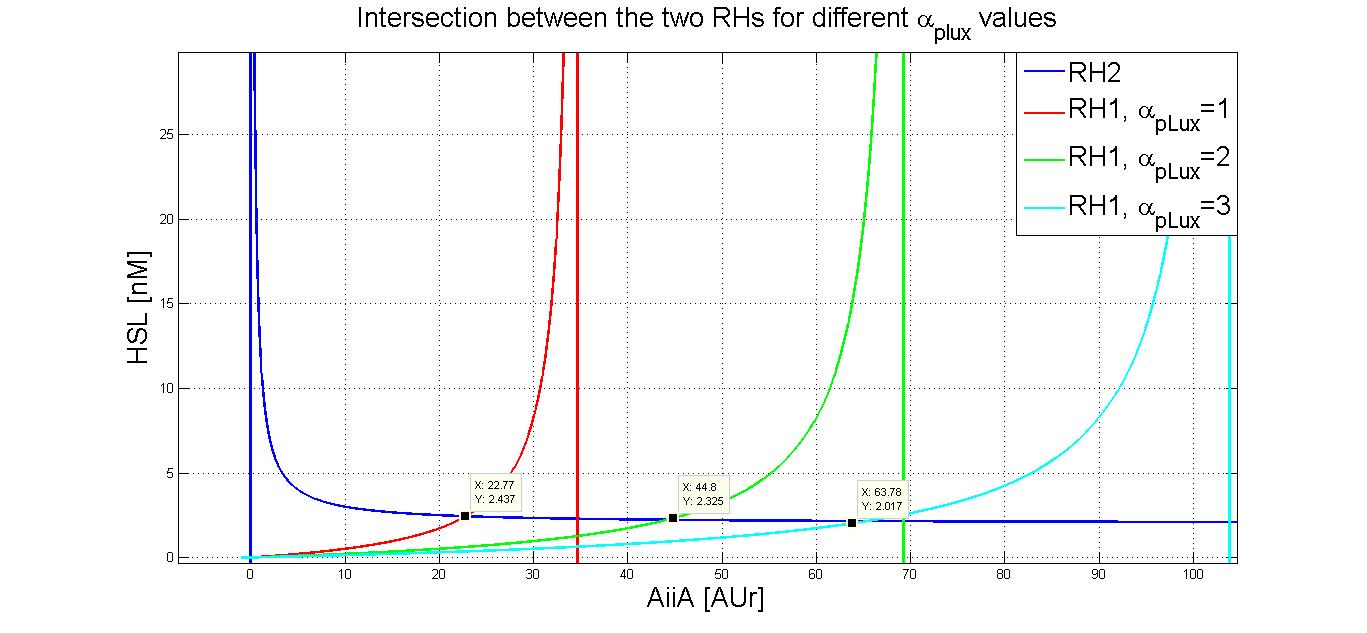
The first equation is independent from the second and third ones, enabling us to directly determine LuxI steady state expression during the exponential growth phase. On the contrary, second and third equations depend each other in defining the value of AiiA and HSL respectively, because the former is a function of HSL, while the latter is a function of AiiA. So we could resolve a system of two equations, first by expliciting one of the two variables with respect to the other, and then substituting its expression in order to determine the other variable possible values. This would bring a complex mathematical formulation, which is not helpful in understanding the influence of the various model parameters on the output HSL. On the other hand, AiiA and HSL values can also be graphically determined from the intersection of the curves derived from these two equations, if we explicit HSL as a function of AiiA (or, alternatively, AiiA as a function of HSL). It is easy to discover that these two curves represent rectangular hyperbolae (the first one only under a simple approximation, explained below) whose tails intersect each other at a particular point, corresponding to the searched values for AiiA and HSL.
centered at O(-d/c;a/c), with the vertical asymptote x=-d/c and the horizontal asymptote y=a/c
From equation (2), we have:
We can introduce the simplification to remove the ηpLux exponent to the entire expression in the right hand side of the equation, thereby obtaining a rectangular hyperbola; even if this leads to a slight change in the curve behaviour, it allows to more clearly understand the relation between HSL and AiiA. As pertains to equation 3, its steady state relationship during the exponential growth is more immediately identifiable as a rectangular hyperbola. Below the two RHs equations are provided, togheter with the table of parameters.
| Parameter | RH1 | RH2 |
| a | VLuxI | (γAiiA+μ)*(kpLux)ηpLux |
| b | VLuxI*kM,AiiA | -αpLux*δpLux*(kpLux)ηpLux |
| c | kcat | -γAiiA-μ |
| d | 0 | αpLux |
| Horizontal asymptote | VLuxI/kcat | a/c=(kpLux)ηpLux |
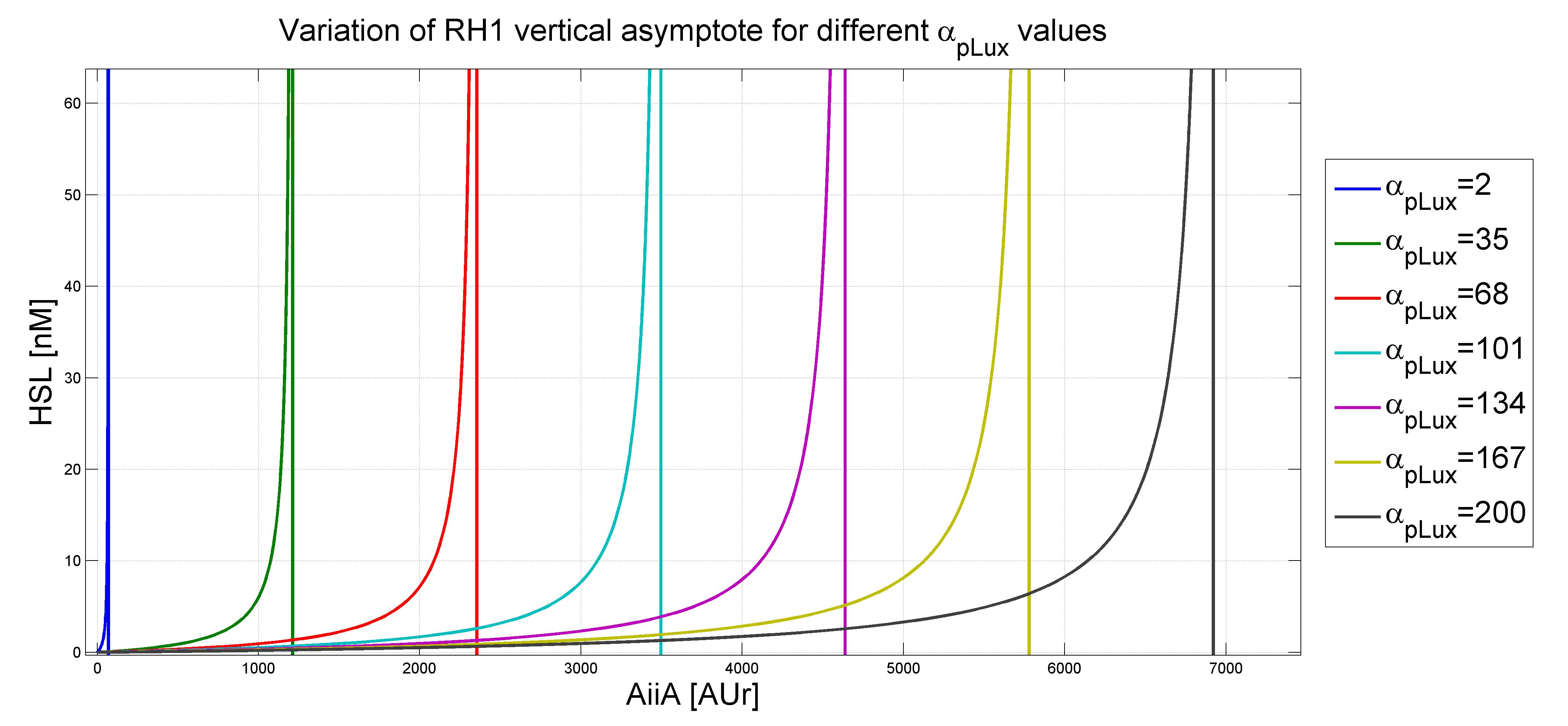
| Vertical asymptote | 0 | -d/c=αpLux/(γAiiA+μ) |
Sensitivity analysis
Now, it is interesting to conduct some qualitative and quantitative considerations about our system sensitivity to its parameters and aTc input signal.
From the above figures, it is also clear that HSL steady state value is not very sensitive to αpLux, at least when this parameter presents values greater than unity, because this brings the two curves to intersect in their low slope regions.
Referring to RH2, the only adjustable asymptote is the horizontal one, that we can move upward or downward by altering VLuxI, which indirectly depends on aTc.
A further deepening in the exponential phase analysis involves determining the characteristics of the input-output relation. Our closed loop system can be realized with two alternative purposes in mind:
- realizing a circuit able to adapt HSL output depending on aTc input concentration. This requires a good sensitivity between input and output.
- designing a robust HSL concentration controller, which is immune to the input noise and offers a constant and defined amount of HSL. In this case HSL level should be appropriately tuned during the design stage, by choosing the correct strength of promoter-RBSx complexes.
Now,again considering the system of equations, it is easy to observe that HSL dependence on aTc input passes through two Hill equations. The former describes aTc driven LuxI synthesis, while the latter models LuxI dependent HSL synthesis rate. Therefore, in order to achieve a high aTc sensitivity, it is advisable to tune aTc and LuxI levels so that they place outside the saturation regions of their Hill curves. In this regard, it is possible to determine a closed form expression relating HSL to aTc, if we hypothesize that both aTc and LuxI are far lower than their respective half-saturation constant (k_ptet and Km), thus simplifying the Hills with a first order relation:
References
- Braun D, Basu S, Weiss R (2005) Parameter estimation for two synthetic gene networks: a case study ICASSP '05 5:v/769-v/772.
- Canton B, Labno A, Endy D. (2008) Refinement and standardization of synthetic biological parts and devices. Nat Biotechnol. 26(7):787-93.
- Danino T, Mondragón-Palomino O, Tsimring L et al. (2010) A synchronized quorum of genetic clocks. Nature. 463(7279):326-30.
- Endler L, Rodriguez N, Juty N et al. (2009) Designing and encoding models for synthetic biology. J. R. Soc. Interface 6:S405-S417.
- Kelly JR, Rubin AJ, Davis JH et al. (2009) Measuring the activity of BioBrick promoters using an in vivo reference standard. J. Biol. Eng. 3:4.
- Pasotti L, Quattrocelli M, Galli D et al. (2011) Multiplexing and demultiplexing logic functions for computing signal processing tasks in synthetic biology. Biotechnol. J. 6(7):784-95.
- Salis H M, Mirsky E A, Voight C A (2009) Automated design of synthetic ribosome binding sites to control protein expression. Nat. Biotechnol.27:946-950.
 "
"