Mathematical modelling plays nowadays a central role in Synthetic Biology, due to its ability to serve as a crucial link between the concept and realization of a biological circuit: what we propose in this page is a modelling approach to our project, which has proven extremely useful and very helpful before and after the "wet lab".

Thus, immediately at the beginning, when there was little knowledge, a mathematical model based on a system of differential equations was derived and implemented using a set of parameters, to validate the feasibility of the project. Once this became clear, starting from the characterization of the single subparts created in the wet lab, some of the parameters of the mathematical model were estimated (the others are known from literature) and they have been fixed to simulate the same model, in order to predict the final behaviour of the whole engineered closed-loop circuit. This approach is consistent with the typical one adopted for the analysis and synthesis of a biological circuit, as exemplified by Pasotti et al 2011.

Therefore here, after a brief overview about the advantages that modelling engineered circuits can bring, we deeply analyze the system of equation formulas, underlining the role and function of the parameters involved.
Experimental procedures for parameter estimation are discussed and, finally, a different type of circuit is presented. Simulations were performed, using ODEs with MATLAB and used to explain the difference between a closed-loop control system model and an open one.

Mathematical modeling reveals fundamental in the challenge for understanding and engineering complex biological systems. Indeed, these are characterized by a high degree of interconnection among the single constituent parts, requiring a comprehensive analysis of their behavior through mathematical formalisms and computational tools

• Simulation: mathematical models allow to analyse complex system dynamics and to reveal the relationships between the involved variables, starting from the knowledge of the behavior of single subparts and from simple hypotesis of their interconnection. (Endler et al, 2009)
• Knowledge elicitation: mathematical models summarize into a small set of parameters the results of several experiments (parameter identification), allowing a robust comparison among different experimental conditions and providing an efficient way to synthesize knowledge about biological processes. Then, through the simulation process, they make possible the re-usability of the knowledge coming from different experiments, engineering complex systems from the composition of its constituent subparts under appropriate experimental/environmental conditions (Braun et al, 2005; Canton et al, 2008)..

Equations (1) and (2) have identical structure, differing only in the parameters involved. They represent the synthesis degradation and diluition of both the enzymes in the circuit, LuxI and AiiA, respectively in the first and second equation: in each of them both transcription and translation processes have been condensed. The corresponding mathematical formalism is analogous to the one used by Pasotti et al 2011, Suppl. Inf., even if we do not take LuxR-HSL complex formation into account, as explained below.

These equations are composed of 2 parts:

1. The first term describes, through Hill's equation formalism, the synthesis rate of the protein of interest (either LuxI or AiiA) depending on the concentration of the inducer (anhydrotetracicline -aTc- or HSL respectively), responsible for the activation of the regulatory element composed of promoter and RBSx. In the parameter table (see below), α refers to the maximum activation of the promoter, while δ stands for its leakage activity (this means that the promoter is slightly active even if there is no induction). In particular, in equation (1), the almost entire inhibition of pTet promoter is given by the constitutive production of TetR by our MGZ1 strain. In equation (2), pLux is almost inactive in the absence of the complex LuxR-HSL.

   Furthermore, in both equations k stands for the dissociation constant of the promoter from the inducer (respectively aTc and HSL in eq. 1 and 2), while η is the cooperativity constant.

   
   

2. The second term in equations (1) and (2) is in turn composed of 2 parts. The former one (γ*LuxI or γ*AiiA respectively) describes, with an exponential decay, the degradation rate per cell of the protein. The latter (μ*(Nmax-N)/Nmax)*LuxI or μ*(Nmax-N)/Nmax)*AiiA, respectively) takes into account the dilution factor against cell growth which is related to the cell replication process.

Here the kinetics of HSL is modeled, through enzymatic reactions either related to the production or the degradation of HSL: based on the experiments performed, we derived appropriate expressions for HSL synthesis and degradation. This equation is composed of 3 parts:

1. The first term represents the production of HSL due to LuxI expression. We modeled this process with a saturation curve in which V_max is the HSL maximum transcription rate, while k_M,LuxI is the dissociation constant of LuxI from the substrate HSL.
   
   
2. The second term represents the degradation of HSL due to the AiiA expression. Similarly to LuxI, k_cat represents the maximum degradation per unit of HSL concentration, while k_M,AiiA is the concentration at which AiiA dependent HSL concentration rate is (k_cat*HSL)/2. The formalism is similar to that found in the Supplementary Information of Danino et al, 2010.
   
   
3. The third term (γ_HSL*HSL) is similar to the corresponding ones present in the first two equations and describes the intrinsic protein degradation.

This is the common logistic population cells growth, depending on the rate μ and the maximum number N_max of cells per well reachable.

The philosophy of the model is to predict the behavior of the final closed loop circuit starting from the characterization of single BioBrick parts through a set of well-designed ad hoc experiments. Relating to these, in this section the way parameters of the model have been identified is presented. As explained before in HP₁, considering a set of 4 RBS for each subpart expands the range of dynamics and helps us to better understand the interactions between state variables and parameters.

These were the first subparts tested. In this phase of the project the target is to learn more about promoter pTet and pLux. Characterizing promoters only is a very hard task: for this reason we considered promoter and each RBS from the RBSx set as a whole (reference to HP₁).
As shown in the figure below, we considered a range of inductions and we monitored, in time, absorbance (O.D. stands for "optical density") and fluorescence; the two vertical segments for each graph highlight the exponential phase of bacterial growth. S_cell (namely, synthesis rate per cell) can be derived as a function of inducer concentration, thereby providing the desired input-output relation (inducer concentration versus promoter+RBS activity), which was modelled as a Hill curve: However, also Relative Promoter Unit (RPU, Kelly 2009) has been calculated as a ratio of S_cell of promoter of interest and the S_cell of BBa_J23101 (reference to HP₄). As shown in the figure above, α, as already mentioned, represents the protein maximum synthesis rate, which is reached, in accordance with Hill's formalism, when the inducer concentration tends to infinite, and, for sufficently high concentrations of inducer. Meanwhile the product α*δ stands for the leakage activity (at no induction), liable for protein production (LuxI and AiiA respectively) even in the absence of inducer. The paramenter η is the Hill's cooperativity constant and it affects the rapidity and ripidity of the switch like curve relating S_cell with the concentration of inducer. Lastly, k stands for the semi-saturation constant and, in case of η=1, it indicates the concentration of substrate at which half the synthesis rate is achieved.

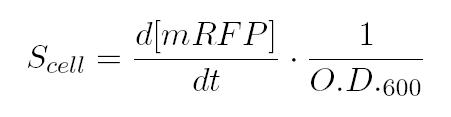
T9002 introduction

LuxI and AiiA tests have been always performed exploiting the well-characterized BioBrick BBa_T9002, by which it's possible to quantify exactly the concentration of HSL. This is a biosensor which receives HSL concentration as input and returns GFP intensity (more precisely Scell) as output. (Canton et al, 2008). According to this, it is necessary to understand the input-output relationship: so, a T9002 "calibration" curve is plotted for each test performed.

AiiA & LuxI