Team:ETH Zurich/Modeling/Analysis

From 2011.igem.org

(Difference between revisions)
(→Stochastic Simulations)
(→Repression Coefficients)
Line 66: Line 66:
|-
|-
|colspan="2"|
|colspan="2"|
-
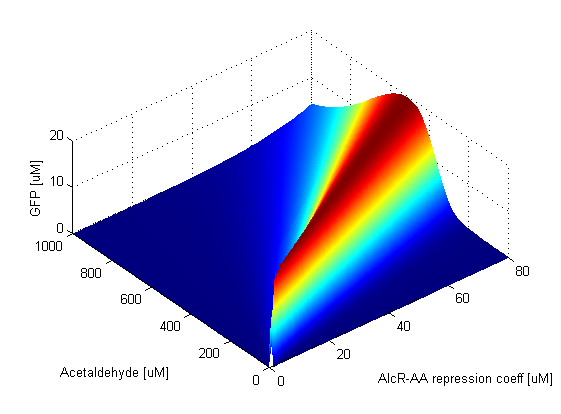
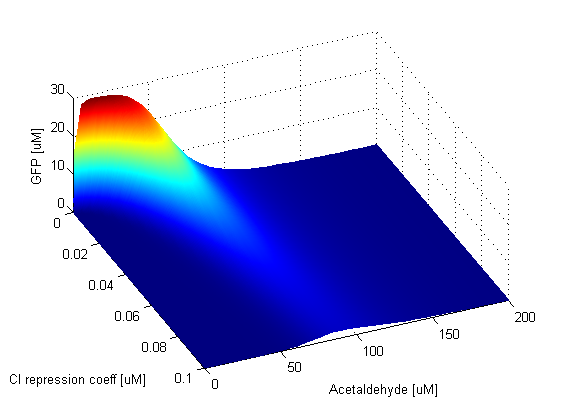
The AlcR-AA repression coefficient affects only the width and position of the GFP band, we can observe that the band widens and shifts to higher acetaldehyde concentrations as the value of the coefficient increases. The TetR repression coeffient seems to have an impact only on the position of the band but not on the amplitude of the peak.  
+
When the AlcR-AA repression coefficient is zero, TetR is always repressed. This in turn means that LacI<sub>M1</sub> is always produced and it represses GFP production. Thus the band is absent. As soon as the AlcR-AA repression coefficient becomes nonzero, the band appears. Since when this value is low, repression of TetR is very efficient, the band is narrow. This can be clearly seen in the graph: the band widens and shifts the position of its peak to higher Acetaldehyde values as the repression becomes weaker. The AlcR-AA repression coefficient influences the lower and upper thresholds which determine where the band is positioned. The amplitude of the GFP band is not affected by the change of this parameter.
 +
 
 +
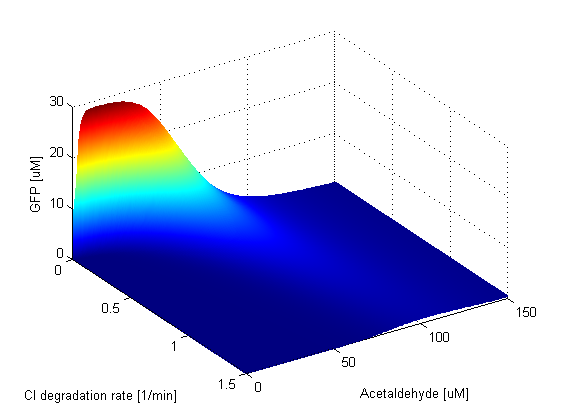
When the TetR repression coefficient is zero, CI and LacI<sub>M1</sub> are completely repressed, thus LacI is free to repress GFP and the band is absent. Since TetR is produced only when the Acetaldehyde concentration is low, if simultaneously the TetR repression coefficient is low, then GFP is repressed, however for higher Acetaldehyde concentrations GFP is produced. This is why in the graph we notice that for low TetR repression coefficients, above a certain Acetaldehyde concentration there is always GFP present. For high values of the TetR repression coefficient the opposite thing happens. GFP is produced for low Acetaldehyde concentrations because in this case repression of CI and LacI<sub>M1</sub> is weak. Thus the TetR repression coefficient has an impact on the width and position of the band, but again the amplitude remains at the same value.  
|- valign="top"
|- valign="top"
|[[File:BetaC.png|thumb|400px|center|'''Figure 8''': Exploring the parameter space of CI repression coefficient]]
|[[File:BetaC.png|thumb|400px|center|'''Figure 8''': Exploring the parameter space of CI repression coefficient]]

Revision as of 12:04, 24 October 2011

Menu image preload Menu image preload Menu image preload Menu image preload Menu image preload Menu image preload


System Analysis
Parameter Sweeps Sensitivity Analysis
We wanted to analyse the effect of the parameters on the output of our system. We achieved this by looking at how the characteristics of the GFP band change when we explore the parameter space of a certain constant and at the sensitivity of GFP to the value of the toxic input substance (acetaldehyde or xylene) .

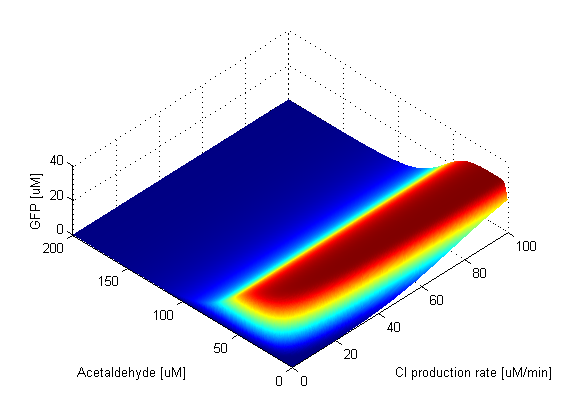
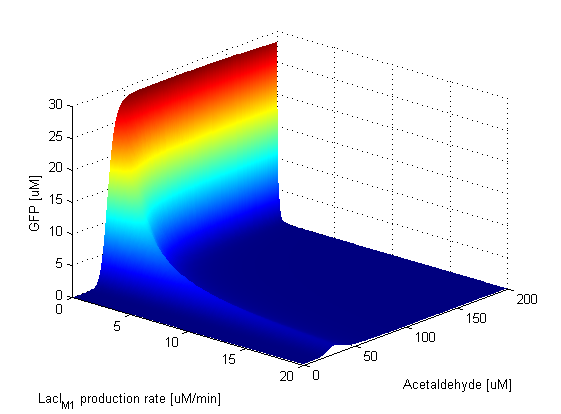
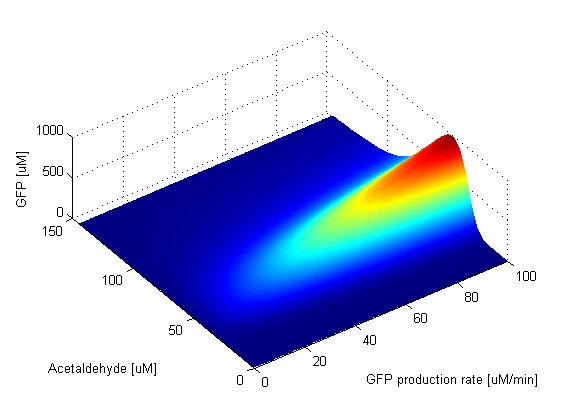
Parameter Sweeps

For the parameters that belong to the band detector module, we explored their parameter spaces to quantify how they affect the features of the GFP band . As we varied each parameter (while keeping the rest constant), we varied also the acetaldehyde input and monitored the GFP output. We analyzed the parameter space only for the model that uses acetaldehyde as an input parameter.

In both models the band is affected in the same way by the parameters of the band detector module. The sensor mechanism can only cause shifts in the band but the band detector module itself is unaffected by the input of the system. The parameter sweeps for the xylene model would therefore be similar to the acetaldehyde model, with differences only for the parameters involved in the sensor mechanism.

In order to speed up the simulations, we used Maple to derive the steady-state formulas for all the relevant species. In this way we were able to obtain the steady-state GFP value simply by knowing the input concentration of Acetaldehyde, without the need to use an ODE solver. Thus we were able to reduce the simulation time from about 30 minutes to under one minute for one parameter sweep.

The following figures show how the band changes with the variation of protein production rates, repression coefficients and degradation rates.


Protein Synthesis Rates

Figure 1: Exploring the parameter space of TetR production rate
Figure 2: Exploring the parameter space of CI production rate

When the TetR production rate is zero, there is no TetR present in the cell, which means that LacIM1 is not repressed so it is free to block GFP production. This can be seen in the graph, since at this value of TetR production the band is absent. As soon as the production rate becomes non-zero, the band appears. The existence of the GFP band is not affected by the value of the TetR production rate, the band is present and the peak stays at a constant amplitude. TetR production rate only affects the width and position of the band which widens and shifts to higher acetaldehyde values as the production rate increases.

When the CI production rate is zero, there is no CI present in the cell, which means that LacI is not repressed, so it is free to block the production of GFP. Thus, the band is absent at this value of CI production rate. After the CI production rate goes above a lower threshold, the band appears. We can observe that above the threshold the GFP band is very robust to the change in CI production rate, maintaining the position and amplitude of the peak at a constant value. The width of the band seems to slightly increase as the CI production rate increases, but at very high values it seems to stay constant.

Figure 3: Exploring the parameter space of LacI production rate
Figure 4: Exploring the parameter space of LacIM1 production rate

When the LacI production rate is zero, only the low-pass branch of the system is in function. This can be seen in the graph, as GFP is produced if Acetaldehyde has a concentration lower than 100 μM. However, as soon as LacI start being produced the band is formed. When the production rate of LacI gets too high, the amplitude of the band decreases, but the position of the peak and the width stay constant.

When the LacIM1 production rate is zero, only the high-pass branch of the system is in fucntion. This means that GFP is produced only when Acetaldehyde is present and its concentration is higher than a low threshold, which is equal to about 20 μM. When LacIM1 appears in the cell, the band is formed. Just as in the case of the LacI production rate, the band seems to maintain its width and the position of its peak, but it decreases its amplitude. This is due to the fact that both LacI and LacIM1 repress GFP production, and if their production rate is high the repression is more efficient.

Figure 5: Exploring the parameter space of GFP production rate

The GFP production rate has an effect only on the amplitude of the band. This is clear from the ODE of the GFP change in time. The amplitude of the GFP is thus directly proportional to the value of the GFP production rate. This can be seen in the graph. When the GFP production rate is zero, naturally no GFP molecules are produced. As soon as the production rate becomes nonzero, the band appears and its amplitude is increasing linearly with the value of the GFP production rate. The width of the band and position of the peak stay fixed.

Repression Coefficients

Figure 6: Exploring the parameter space of AlcR-AA repression coefficient
Figure 7: Exploring the parameter space of TetR repression coefficient

When the AlcR-AA repression coefficient is zero, TetR is always repressed. This in turn means that LacIM1 is always produced and it represses GFP production. Thus the band is absent. As soon as the AlcR-AA repression coefficient becomes nonzero, the band appears. Since when this value is low, repression of TetR is very efficient, the band is narrow. This can be clearly seen in the graph: the band widens and shifts the position of its peak to higher Acetaldehyde values as the repression becomes weaker. The AlcR-AA repression coefficient influences the lower and upper thresholds which determine where the band is positioned. The amplitude of the GFP band is not affected by the change of this parameter.

When the TetR repression coefficient is zero, CI and LacIM1 are completely repressed, thus LacI is free to repress GFP and the band is absent. Since TetR is produced only when the Acetaldehyde concentration is low, if simultaneously the TetR repression coefficient is low, then GFP is repressed, however for higher Acetaldehyde concentrations GFP is produced. This is why in the graph we notice that for low TetR repression coefficients, above a certain Acetaldehyde concentration there is always GFP present. For high values of the TetR repression coefficient the opposite thing happens. GFP is produced for low Acetaldehyde concentrations because in this case repression of CI and LacIM1 is weak. Thus the TetR repression coefficient has an impact on the width and position of the band, but again the amplitude remains at the same value.

Figure 8: Exploring the parameter space of CI repression coefficient
Figure 9: Exploring the parameter space of LacI repression coefficient

We observe that the GFP band is sensitive to the CI repression coefficent and appears only for low values of it. The LacI repression coefficient does not have a high impact on the band as it only widens it when the parameter value gets larger.

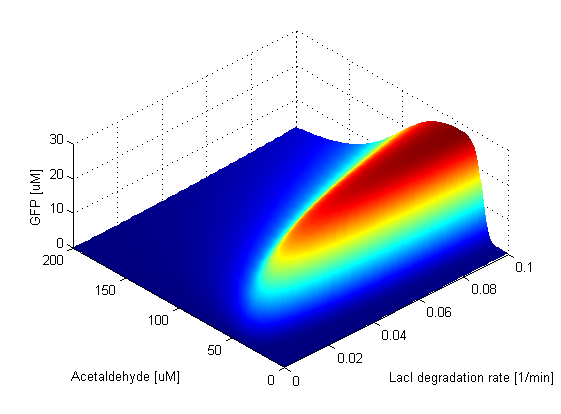
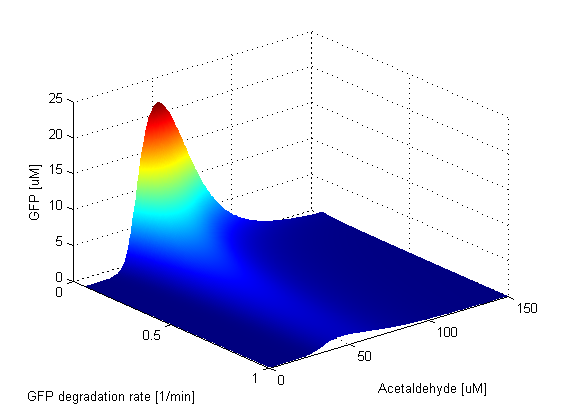
Protein Degradation Rates

Figure 10: Exploring the parameter space of TetR degradation rate
Figure 11: Exploring the parameter space of CI degradation rate

The degradation rate of TetR does not influence the existence of the band and the amplitude of its peak. The GFP band seems to be present at all parameter values, however its position and width change in the region of low degradation rates, but it is completely robust at higher concentration values. The CI degradation rate allows the band to appear only when its value is low, at higher rates the band formation is stopped.

Figure 12: Exploring the parameter space of LacI degradation rate
Figure 13: Exploring the parameter space of GFP degradation rate

We notice that the amplitude of the GFP peak and the bandwidth exhibit positive correlation with respect to the LacI degradation rate. As expected, there is a strong negative correlation between the height and width of the peak and the GFP degradation rate, since the GFP band can exist only of the GFP molecules are not degraded too quickly.

Coupled parameter variation

With doing the parameter sweeps for individual parameters, we saw how robust our system is with respect to a particular paramter. But in reality, when parameters vary, they usually don't vary alone, but they are coupled (i.e more parameters vary simultaneously). One way to incorporate this fact in our model is to couple the expression rates of the proteins according to the plasmid they are expressed on and vary them together.

Stochastic Simulations

Besides the parameter space search, we performed another type of analysis in order to verify that our system is robust and that it is not bistable. We were especially interested at the GFP band and whether it is always there.

We did stochastic simulations to see how our system reacts to noise and how it responds to perturbations. For a certain acetaldehyde concentration (which gives the peak of the band) we wanted to see how the GFP peak value varies over long time period when we consider stochasticity.

For the stochastic simulations we used the software Dizzy, to which we gave as an input file an SMBL file with the description of our system. Moving from deteministic to stochastic simulations, we had to change several things in the SBML file. For instance, we had to convert all the concentrations into number of molecules (and round them) and also separate the ODEs for the species into ODEs for distinct reaction channels (i.e. separate degradation from activation/repression) etc.

We started with a deterministic simulation to take the deterministic steady states of the species, after 5000 min(the acetaldehyde amount was the one that leads to the maximal GFP value, i.e the peak of the band). Starting from deterministic steady states, we performed a stochastic simulation with Gillespie-direct algorithm for 10000 min in order to get the stochastic steady states. After that, we restarted the stochastic simulation having the stochastic steady state values as our initial and simulated for 100 000 more minutes (storing the GFP values every 10th minute). We collected all the GFP values from the last simulation and plotted them in a histogram (Figure 1).


Sensitivity Analysis

Sensitivity analysis is a technique that studies the change of the output (or any observable) of a certain function with the variation of a certain parameter. It gives us an overview of how sensitive the model is with respect to the parameter, i.e. what the impact of the parameter is. The sensitivity is defined as the partial differential equation of the observable with respect to a certain parameter.

We performed sensitivity analysis with respect to acetaldehyde or xylene. For different input concentrations we monitored the change in the GFP output (dGFP/dAcetaldehyde or dGFP/dXylene).


Figure 14: Sensitivity analysis with respect to acetaldehyde


For the acetaldehyde model, it can be seen from the above figure that the sensitivity is highest when GFP rises. For the peak itself (at [AA] = 1000uM), the sensitivity drops down and then rises again once GFP concentration starts decreasing. This tells us that the GFP concentration level is most sensitive to acetaldehyde at those concentrations where GFP rises and falls.

Retrieved from "http://2011.igem.org/Team:ETH_Zurich/Modeling/Analysis"