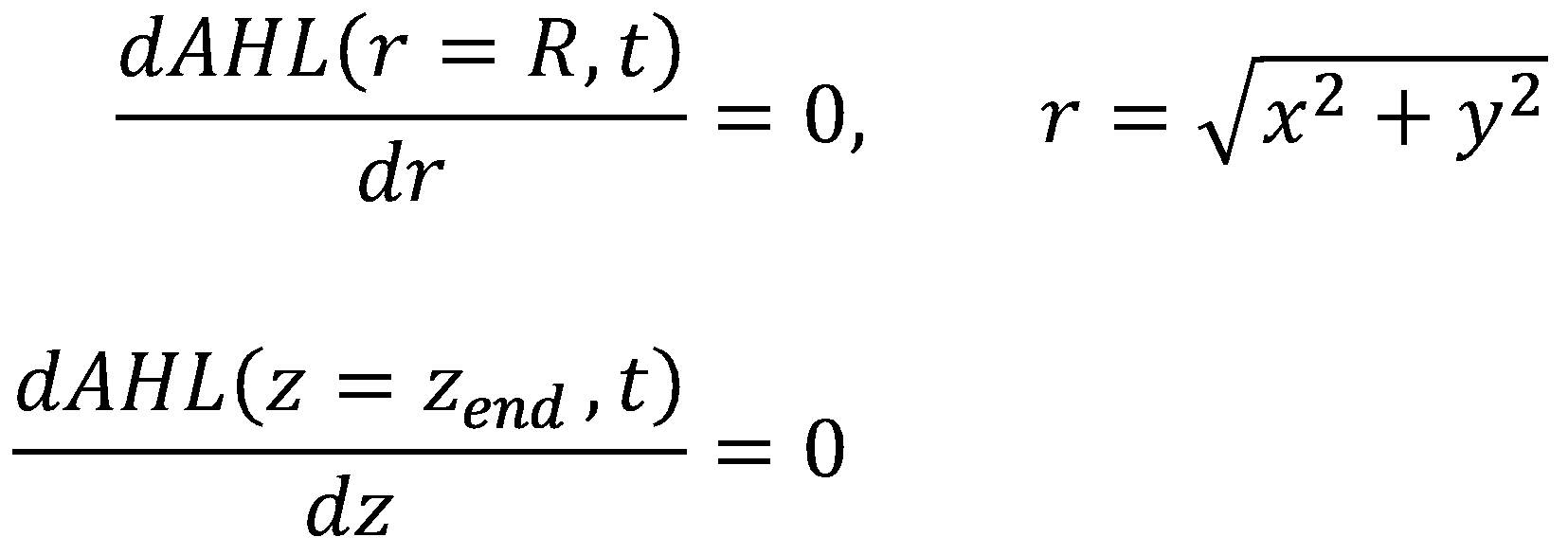Combined Model

Now that both the single-cell model and the reaction-diffusion model for the gradient formation are complete, we can integrate both of them into a combined model. This implies both adding a diffusion-degradation system for AHL as well as locally coupling all the ordinary differential equations from the single-cell model. We hope to gain some insight into the dynamics and steady-state of the GFP peak resulting from the band-pass filter on acetaldehyde concentration. Additionally, we evaluate the AHL-diffusion-based RFP alarm system. Since these simulations take a lot of time, for now, we only worked with acetaldehyde. However, xylene or arabinose could easily be added by incorporating the appropriate single-cell model and diffusion/degradation mechanism.

The spatiotemporal model basically predicts that our system will work, having a GFP band moving depending on the acetaldehyde concentration in the reservoir and an RFP alarm that activates once out of detection range, i.e. when the GFP band disappears:

Video I: 41 steady state simulations, from 1 to 400 mg/l acetaldehyde concentration in reservoir in 10 mg/l steps: Relative GFP fluorescence (Blue: 0%, Green: 100%), Channel diameter: 1 mm, Channel length: 1 cm

Video II: 41 steady state simulations, from 1 to 400 mg/l acetaldehyde concentration in reservoir in 10 mg/l steps: RFP fluorescence, Channel diameter: 1 mm, Channel length: 1 cm

Read on to see the derivation of this result!

Combining the Models

Local Band Detector

We start off with the equations for the band detector with acetaldehyde input in the single-cell model. Given the local acetaldehyde concentration, we can evaluate them locally at each point in the system:

Acetaldehyde PDE

Next we add all the equations from the reaction-diffusion (or in our case more specifically: degradation-diffusion) model for acetaldehyde, including a partial differential equation, into the mix, which gives us the local acetaldehyde concentration required above. This simplifying coupling assumes that diffusion of acetaldehyde into the E. coli cells is fast compared to the rest of our dynamics.

AHL PDE

For AHL, we also have to set up a partial differential equation-based reaction-diffusion system. Similar to acetaldehyde diffusion, we assume that AHL diffusion into and out of cells is fast, i.e. we do not model this diffusion process explicitly. Thus, in contrast to the single-cell model, we only use one species called AHL instead of an internal AHL concentration AHLi and an external AHL concentration AHLe.

Similarly to the acetaldehyde reaction-diffusion case, we start off with the general partial differential equation describing reaction-diffusion dynamics:

Diffusion

The diffusive term obviously is the same as for acetaldehyde, except for a different isotropic diffusion constant for AHL at 25°C D_AHL, which replaces the one for acetaldehyde:

Reaction

The reaction term we model with linear intra- and extracellular degradation, with respective degradation coefficients k_s0 and γ_AHL,ext, as well as AHL production proportional to LuxI with AHL production coefficient k_s1:

Initial and Boundary Conditions

For the initial condition, we choose the AHL level the cells would have immediately before we connect the agarose-filled channel to the reservoir. As we can assume that there is a high number of cells in the channel, and that the cells had some time to grow, we may assume that the AHL level has converged to a steady state:

We satisfy this initial condition by setting the AHL level to 0 initially and simulating till steady state is reached, without having any acetaldehyde present. We then use this as a starting state for the dynamics. Note that the intracellular starting state for the other species in the single-cell-model is also steady state with no acetaldehyde input.

For the boundary conditions, we leave our options for tuning the system open by allowing the reservoir (again located at z = 0) to have a constant level of AHL (Dirichlet Boundary Condition):

For the walls, we enforce the same boundary conditions as in the diffusion model for acetaldehyde (Neumann Boundary Conditions):

Local AHL-based Alarm

Finally we add the rest of the equations from the single-cell model, which are the ones for the local AHL-based alarm system minus the ones for AHL diffusion, which we now simulate spatiotemporally and without membrane diffusion:

Full Model

Combining all of the equations yields the following system:

Simulations & Results

Acetaldehyde PDE & GFP Band Detector

Comparison with Single-Cell Model

First we compare if the GFP band in the spatiotemporal reaction-diffusion model occurs for the same local acetaldehyde concentration as in the single-cell model. In the initial single-cell model, the band occurs from 500μM to 1500μM. From Figure 1 one can see that the band in the spatiotemporal model occurs in the same range of acetaldehyde concentration:

Steady State Sweep

After sanity-checking the model, we first only considered the GFP band detector part of our system. We are interested in its behavior depending on varying input concentration of acetaldehyde in the reservoir. Thus we simulated the channel for different input acetaldehyde concentrations in the reservoir. We varied the value from 1 to 2500 mg/l and computed the steady state for these and 98 intermediate values, yielding 100 spatiotemporal steady state simulations in total:

From Video 1 we can see that we can detect a 2500-fold difference in acetaldehyde concentration and that the GFP peak produced by the band-pass filter moves through the channel uniformly, with the exception of very low and very high concentrations. This is when the band moves in and out of detection range of our system.

Toxicity: Results Update

Acetaldehyde PDE & GFP Band Detector

In hand with the biologists in our team, we noticed that some acetaldehyde concentrations may be toxic and corrected the single-cell model. we update the combined model with the new parameters from the toxicity analysis in the single-cell model. Also, we update the channel dimensions according to the results from the analysis of the reaction-diffusion model of acetaldehyde.

Steady State Sweep

For the new system, we vary the acetaldehyde concentration from 1 mg/l to 400 mg/l in 41 steps, and for each step computed the steady state of the system in the channel. We now plot relative GFP florescence at steady state with the acetaldehyde reservoir located at the front left:

The sensing range we found for the new channel dimensions with the updated single-cell model was 1 to 400 mg/l of acetaldehyde. The peak GFP expression the model predicts is roughly 1000-fold over base expression level.

Full System & AHL-based RFP-Alarm

Steady State Sweep

Finally, we plot the RFP fluorescence from the same simulation, again running the system to steady state for acetaldehyde levels in the reservoir stated above:

For the last two steady state simulations, i.e. 390 mg/l and 400 mg/l, as the GFP band vanishes the RFP alarm completely activates. This shows that our desired behavior is reproduced by the 3D reaction-diffusion model with SmoColi cells in the channel.

Back to iGEM	Our Sponsors