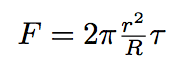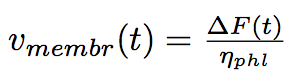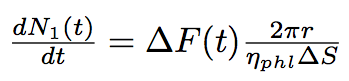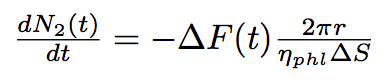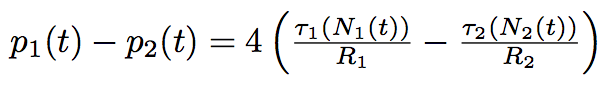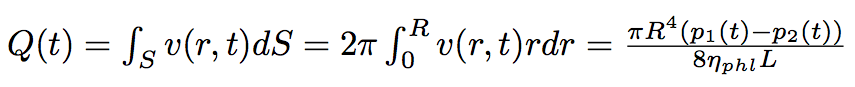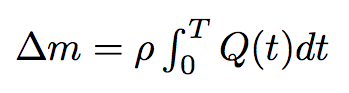Team:Paris Bettencourt/Modeling/Assisted diffusion/Pressure differential
From 2011.igem.org
(Created page with "{{:Team:Paris_Bettencourt/tpl_test}} __NOTOC__ <html> == Back to the classical physics == To deduce the force exercising on the tube from membranian pressure, please refer to ...") |
|||
| Line 2: | Line 2: | ||
__NOTOC__ | __NOTOC__ | ||
| - | |||
== Back to the classical physics == | == Back to the classical physics == | ||
| Line 63: | Line 62: | ||
where T is the time of the process. | where T is the time of the process. | ||
| - | |||
| - | |||
Revision as of 15:30, 23 October 2011

Back to the classical physics
To deduce the force exercising on the tube from membranian pressure, please refer to an explanation figure below :
Here T is a surface tension, N is a resulting force of the area of the tube attachment to the bacterium, Δα or α is the half of the angle with a vertex in the center of the bacterium and between the tube extremities. Only this zone is giving a non-compensated contribution to the resulting force.
So the force exercising on the tube is given by the formula :
where r is the tube radius, R is the bacterium radius.
At first approximation we can consider the process a serie of quasi equilibrium states, that it is rather slow that acceleration of the membrane is zero. We find the speed of the tube membrane at every moment of time out of the second Newton's law :
where ΔF is the difference of the forces applied to the extremities of the tube.
The number of phospholipids in two bacteria will change according to these equations :
where N1, N2 are numbers of phospholipids on the membrane of the first and the second bacterium corrispondingly, ΔS is the surface per one phospholipid one the tube.
Cutting the whole period of time of our process into laps of time dt we should solve the Poiseuille equation each time reevoluating the difference of pressure :
The Poiseuille equation :
where L is the total length of the nanotube, r is the distance from the center line of the nanotube, R is the radius of the nanotube.
The volume flow of the liquid passed through the nanotube is :
By integrating the last formula in time we will get the mass of the liquid passed from one bacterium to another :
where T is the time of the process.
 "
"