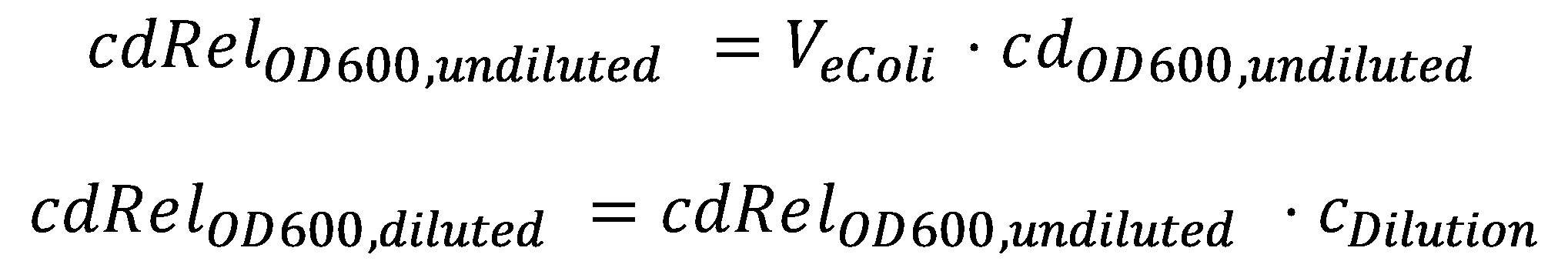Team:ETH Zurich/Modeling/Microfluidics
From 2011.igem.org
(→Steady State) |
(→Simulation) |
||
| Line 87: | Line 87: | ||
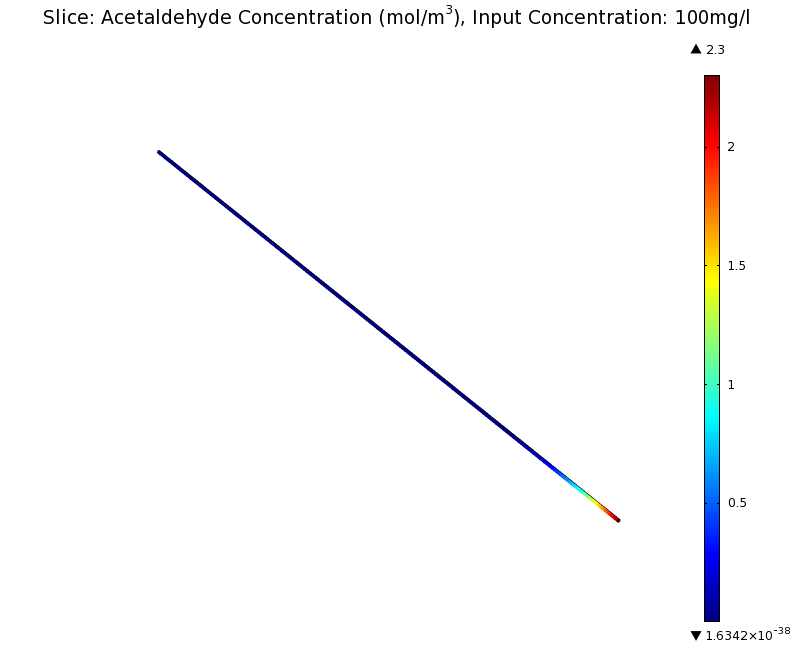
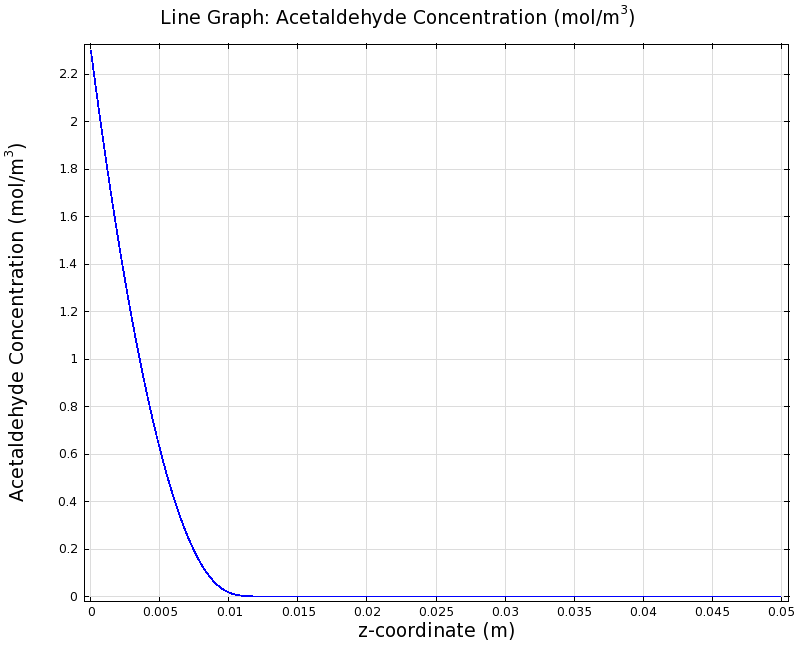
=== Simulation for 100 mg/l of acetaldehyde, standard channel width === | === Simulation for 100 mg/l of acetaldehyde, standard channel width === | ||
{|style="border: none;" align="center" | {|style="border: none;" align="center" | ||
| - | |[[File:ETHZ-AcAl_100mgl_SS.png|center| | + | |[[File:ETHZ-AcAl_100mgl_SS.png|center|400px|thumb]] |
| - | |[[File:ETHZ-AcAl_100mgl_SS_profile.png|center| | + | |[[File:ETHZ-AcAl_100mgl_SS_profile.png|center|400px|thumb]] |
|} | |} | ||
=== Simulation for 100 mg/l of acetaldehyde, 0.1x standard channel diameter (200μm) === | === Simulation for 100 mg/l of acetaldehyde, 0.1x standard channel diameter (200μm) === | ||
{|style="border: none;" align="center" | {|style="border: none;" align="center" | ||
| - | |[[File:ETHZ-AcAl 100mgl_SS_thinner_10x.png|center| | + | |[[File:ETHZ-AcAl 100mgl_SS_thinner_10x.png|center|400px|thumb]] |
| - | |[[File:ETHZ-AcAl_100mgl_SS_thinner_10x_profile.png|center| | + | |[[File:ETHZ-AcAl_100mgl_SS_thinner_10x_profile.png|center|400px|thumb]] |
|} | |} | ||
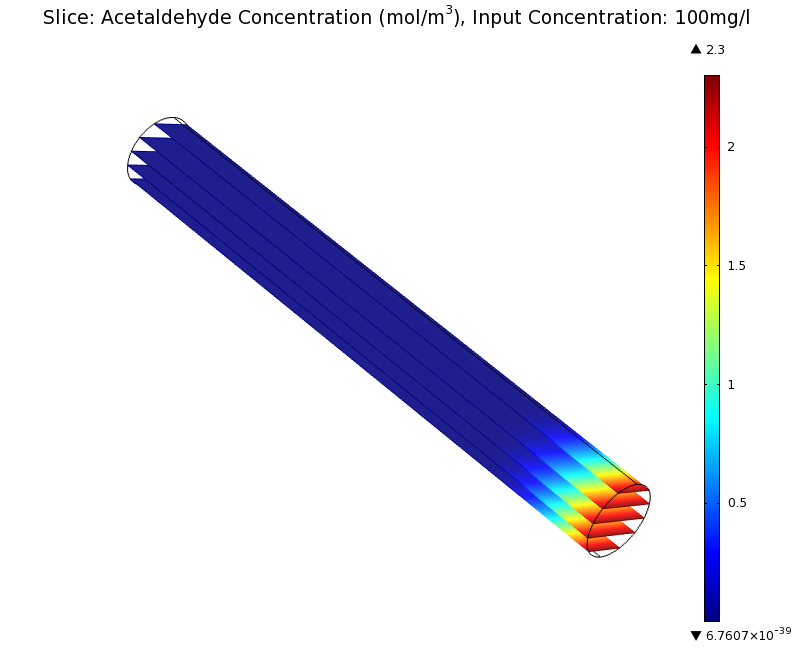
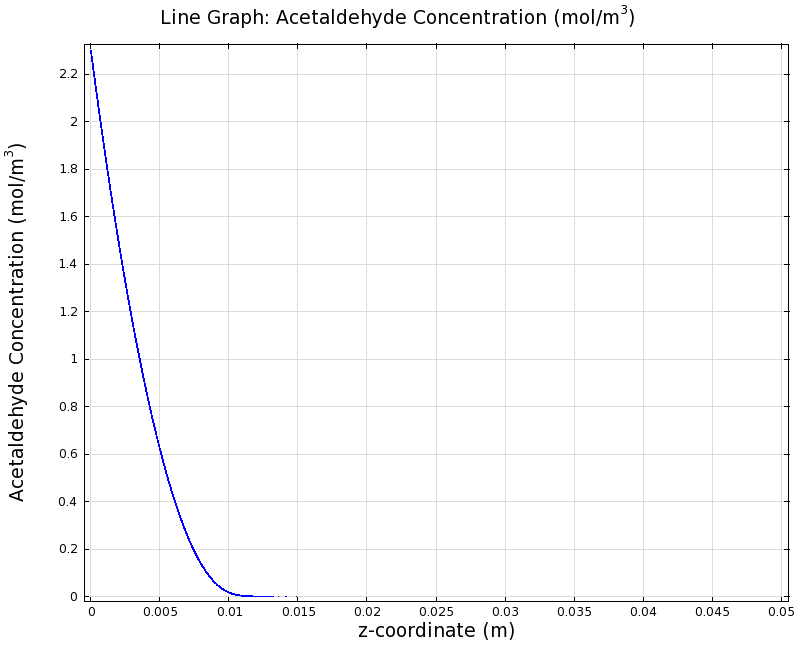
=== Simulation for 100 mg/l of acetaldehyde, 3x standard channel diameter (6mm) === | === Simulation for 100 mg/l of acetaldehyde, 3x standard channel diameter (6mm) === | ||
{|style="border: none;" align="center" | {|style="border: none;" align="center" | ||
| - | |[[File:ETHZ-AcAl 100mgl_SS_thicker_3x.png|center| | + | |[[File:ETHZ-AcAl 100mgl_SS_thicker_3x.png|center|400px|thumb]] |
| - | |[[File:ETHZ-AcAl_100mgl_SS_thicker_3x_profile.png|center| | + | |[[File:ETHZ-AcAl_100mgl_SS_thicker_3x_profile.png|center|400px|thumb]] |
|} | |} | ||
Revision as of 22:49, 19 September 2011
| Microfluidics Model |
| |||||
| In our first spatiotemporal model, we wanted to find out if an Acetaldehyde gradient would be formed at all. The idea was to generate it as an equilibrium of Acetaldehyde diffusion out of the reservoir into our channel and Acetaldehyde degradation by the cells in it. In order to answer this question, we modeled a spatiotemporal reaction-diffusion system in 3D with COMSOL Multiphysics. | ||||||
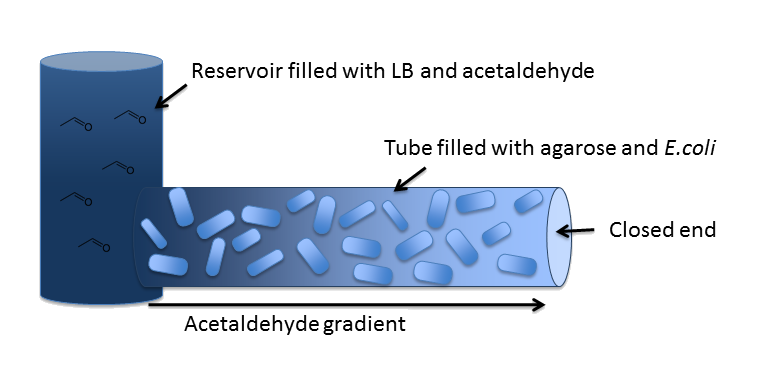
OverviewIn our inital model, we chose a 5 cm long cylindrical channel with a radius of 1 mm (or equivalently 2 mm diameter). This channel is connected to a reservoir filled with medium and the toxic molecule. For the purpose of modeling the diffusion and degradation of the toxic molecule in the channel, we assumed that the reservoir has constant toxic molecule concentration (or equivalently has infinite size). In our system, we degrade a toxic substance diffusing from a reservoir into a block of e. Coli cells immobilized in agarose in order to generate a toxic substance gradient. The two substances we consider in our model are acetaldehyde and xylene. In our first microfluidics model we conducted a feasibility study and thus only investigated acetaldehyde degradation. |
DiffusionFirst of all, we have to model diffusion of Acetaldehyde from the reservoir to the closed end of the microfluidics channel. The relevant partial differential equation is the one for isotropic diffusion, i.e. diffusion that is uniform in all directions: For the relevant diffusion parameter, DAcAl, see the microfludics model section on the parameters page. |
DegradationCell DensityIn order to able to determine how much Acetaldehyde our smoColi cells are able to degrade, we first need to determine the cell density of the immobilized cells in agarose. For this calculation, we assume we have a cell culture with OD600 with which we fill the channel. Parameter-wise, to determine the relative cell density in the channel voume, we need to know:
A parameter we can choose suitably is the dilution of the cells in agarose, cDilution. Then we can calculate the relative cell density in the smoColi-agarose-filled microfluidics channel: Enzymatic DegradationNow that we know what the cell concentration in the channel is, we can model the degradation of the toxic molecule by the cell culture in agarose. This process, together with diffusion of more toxic molecules from the reservoir, will finally generate the toxic molecule gradient. In our enzymatic degradation model, we assume diffusion into the cells is fast compared to the degradation process. The degradation process then is modeled using Michaelis-Menten enzyme reaction kinetics: The constants are the usual ones for Michaelis-Menten-type reactions:
Estimation of vmax,AcAlFor the degradation of acetaldehyde we only had direct literature values for KM,AcAl, but not for vmax,AcAl. However, we did find values for the specific activity Kcat,AcAl of acetaldehyde dehydrogenase in e. Coli, which we used to estimate vmax,AcAl with the following equation: Here, [E]T is the total enzyme concentration of acetaldehyde dehydrogenase. This value we derived from the concentration of acetaldehyde dehydrogenase in cell extract, which we in turn calculated by estimating the number of acetaldehyde dehydrogenase enyzmes nADH in a single e. Coli cell. The number of acetaldehyde dehydrogenase enzymes nADH in a single e. Coli cell was estimated from diluted cell-free extract with dilution ratio dilExtract and diluted concentration of [ADH]Extract. |
ModelNow that we have values for all of the parameters, we can finally combine both the partial differential equation for diffusion and the local ordinary differential equation for reaction into the spatiotemporal reaction-diffusion (or in our case, degradation-diffusion) system: |
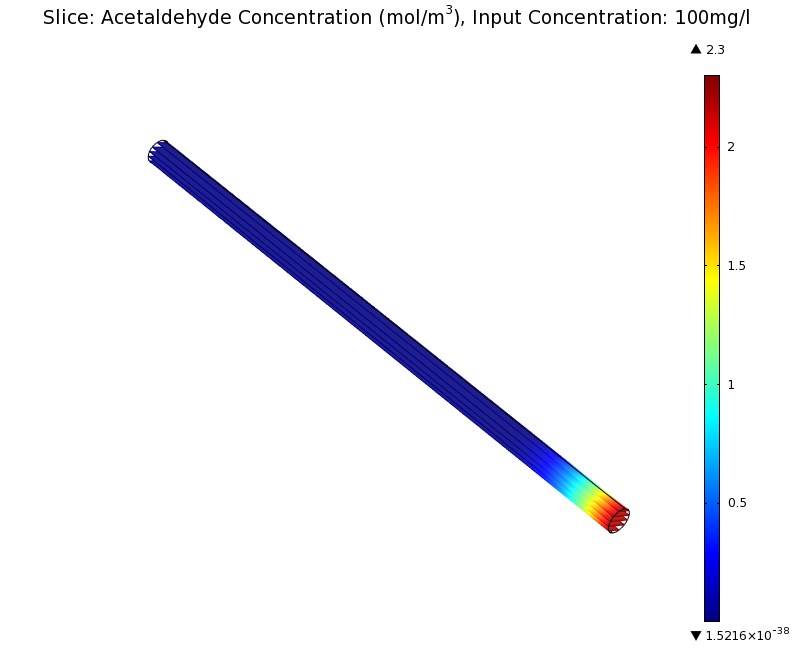
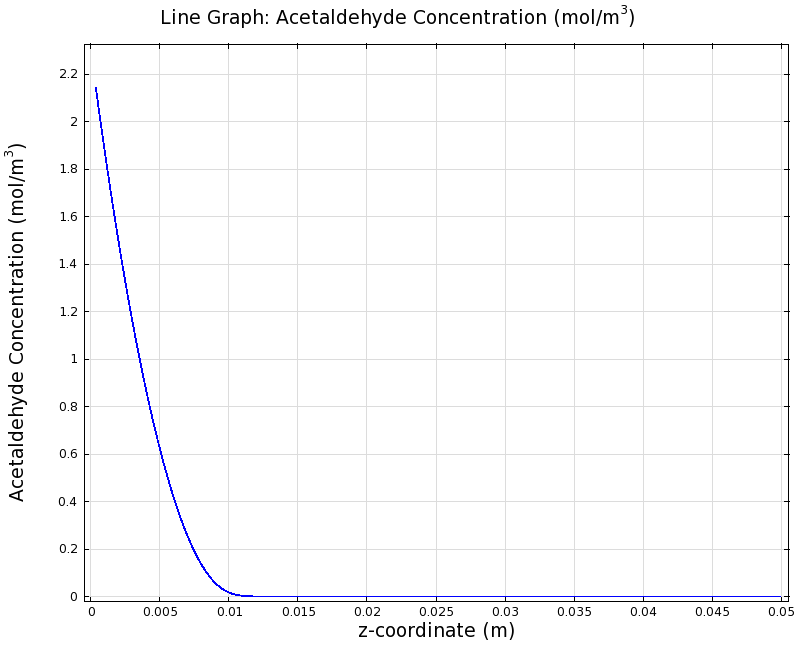
SimulationTo see if we can indeed create an acetaldehyde gradient, we first solved for the gradient steady state in the channel. We chose an acetaldehyde concentration of 100 mg/l for the reservior in these simulations. Steady StateFirst, we simulated the steady state of the acetaldehyde gradient in channels with different diameters. Our Simulation for 100 mg/l of acetaldehyde, standard channel widthSimulation for 100 mg/l of acetaldehyde, 0.1x standard channel diameter (200μm)Simulation for 100 mg/l of acetaldehyde, 3x standard channel diameter (6mm)We can see that the diameter does not influence the mean dynamics of the acetaldehyde gradient (observant readers will notice that the concentration at the end of the channel is not exactly the same - this effect is a result of numerical imprecision). We note that there may be stochastic behavior for very thin channels, since there will be only very few cells. For the channel diameter we chose, a mean field approximation should be sufficient though, as the amount of cells involved in the degradation is sufficiently high. DynamicsWe were also interested in finding out the time scale which is needed to create the gradient. Therefore we also analyzed the dynamics in a spatiotemporal reaction (degradation) - diffusion simulation. |
 "
"