Team:ETH Zurich/Modeling/Stochastic
From 2011.igem.org
(→Analysis of Results) |
(→Analysis of Results) |
||
| (32 intermediate revisions not shown) | |||
| Line 3: | Line 3: | ||
{{:Team:ETH Zurich/Templates/SectionStart}} | {{:Team:ETH Zurich/Templates/SectionStart}} | ||
= Stochastic Analysis = | = Stochastic Analysis = | ||
| - | '''Besides the parameter space search, we performed another type of analysis in order to verify that our system is robust and that it is | + | '''Besides the parameter space search, we performed another type of analysis in order to verify that our system is robust and that it is monostable (i.e. it has only one steady state). We were especially interested in the GFP band, whether it is always present and whether the amount of GFP produced in the cells for different concentrations of Acetaldehyde has large fluctuations. Because gene expression is an intrinsically stochastic process, we performed stochastic simulations to see how our system reacts to noise and how it responds to perturbations.''' |
<br> <br> | <br> <br> | ||
| - | '''The following results show that our system is indeed robust and it does not have bifurcations.''' | + | '''The following results show that our system is indeed robust to noise and it does not have bifurcations.''' |
{{:Team:ETH Zurich/Templates/SectionEnd}} | {{:Team:ETH Zurich/Templates/SectionEnd}} | ||
{{:Team:ETH Zurich/Templates/SectionStart}} | {{:Team:ETH Zurich/Templates/SectionStart}} | ||
= Method = | = Method = | ||
| - | For the stochastic simulations we used the [http://magnet.systemsbiology.net/software/Dizzy/ Dizzy] software, to which we gave as an input an SBML file with the description of our system. Moving from deterministic to stochastic simulations we had to change several things in the SBML file. Firstly, we exported the SBML file to a CMDL format.Next, we converted the species values as well as the production rates and repression coefficients from | + | For the stochastic simulations we used the [http://magnet.systemsbiology.net/software/Dizzy/ Dizzy] software, to which we gave as an input an SBML file with the description of our system. Moving from deterministic to stochastic simulations we had to change several things in the SBML file. Firstly, we exported the SBML file to a CMDL format.Next, we converted the species values as well as the production rates and repression coefficients from concentrations (in μM) to number of molecules. Since our initial system was described in terms of ODEs, we also had to change this by separating the system into distinct reaction channels (i.e. separate degradation from activation/repression) and specifying the reaction rates. |
<br> <br> | <br> <br> | ||
With the new description of the system, we could start the simulations. For analyzing the robustness of the system, we chose 5 strategic Acetaldehyde concentrations (see Figure 1), and for each of them we performed stochastic simulations. We selected the following Acetaldehyde concentrations: | With the new description of the system, we could start the simulations. For analyzing the robustness of the system, we chose 5 strategic Acetaldehyde concentrations (see Figure 1), and for each of them we performed stochastic simulations. We selected the following Acetaldehyde concentrations: | ||
| Line 21: | Line 21: | ||
[[File:GFPmlabel.png|thumb|900px|center|'''Figure 1''': GFP versus Acetaldehyde. The red squares denote the 5 Acetaldehyde concentrations for which we simulated the time course of GFP steady state in stochastic mode.]] | [[File:GFPmlabel.png|thumb|900px|center|'''Figure 1''': GFP versus Acetaldehyde. The red squares denote the 5 Acetaldehyde concentrations for which we simulated the time course of GFP steady state in stochastic mode.]] | ||
| - | In order to be sure that we are indeed simulating the time course of the stochastic steady state, and that we are not in the transient regime, we implemented the following approach: | + | In order to be sure that we are indeed simulating the time course of the "stochastic steady state", and that we are not in the transient regime, we implemented the following approach: |
* We ran a deterministic simulation for 5000 minutes (~ 83 hours) to get to the deterministic steady state. We took over the concentration values for the last time point as new initial conditions for the next simulation. | * We ran a deterministic simulation for 5000 minutes (~ 83 hours) to get to the deterministic steady state. We took over the concentration values for the last time point as new initial conditions for the next simulation. | ||
* We ran a stochastic simulation for 10000 minutes (~ 7 days), to make sure that we are somewhere around the “stochastic steady state”. Once again we took over the concentration values for the last time point as new initial conditions for the next simulation. | * We ran a stochastic simulation for 10000 minutes (~ 7 days), to make sure that we are somewhere around the “stochastic steady state”. Once again we took over the concentration values for the last time point as new initial conditions for the next simulation. | ||
| - | * We ran a long stochastic simulation for 100000 minutes (~ 70 days) | + | * We ran a long stochastic simulation for 100000 minutes (~ 70 days) storing the molecule numbers of the species every minute. |
| - | + | <br> | |
| + | For the stochastic simulations we used the "Gillespie-direct" option, since this gives an exact solution, compared to the other solvers which only approximate the solution. | ||
{{:Team:ETH Zurich/Templates/SectionEnd}} | {{:Team:ETH Zurich/Templates/SectionEnd}} | ||
| Line 31: | Line 32: | ||
= Simulations = | = Simulations = | ||
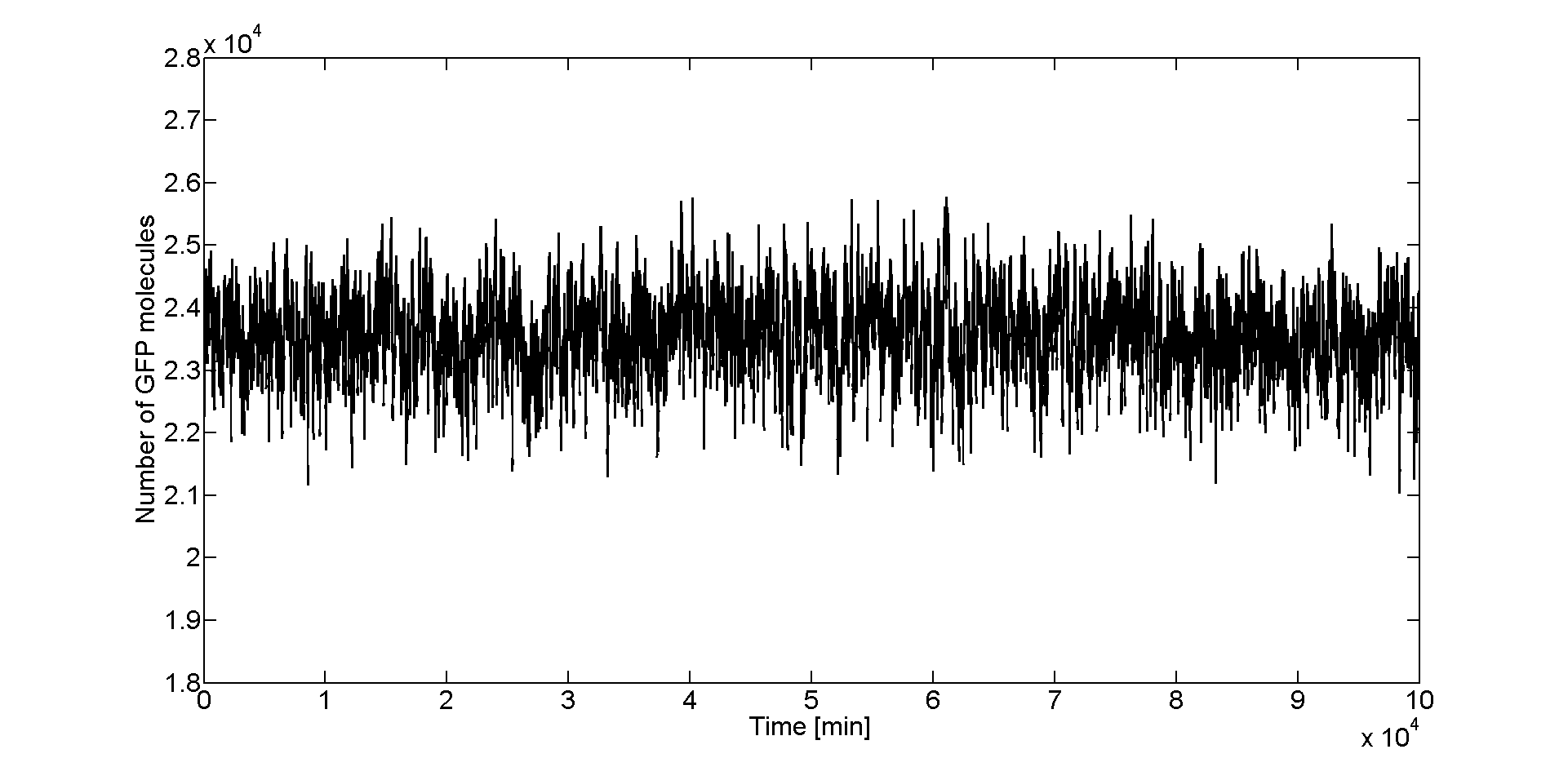
| - | After we obtained the samples with Dizzy, we loaded the data in Matlab to analyze it. To get an initial feeling of how the system behaves in the stochastic regime, we plotted the GFP molecule numbers | + | After we obtained the samples with Dizzy, we loaded the data in Matlab to analyze it. To get an initial feeling of how the system behaves in the stochastic regime, we plotted the GFP molecule numbers as function of time. In Figure 2 we can see that for the peak of the band (Acetaldehyde = 46 μM), GFP values fluctuate around a mean value which is about 23500 molecules. |
[[File:Gfpfl50.png|thumb|900px|center|'''Figure 2''': Stochastic simulation of GFP steady state for an Acetaldehyde concentration of 46 μM.]] | [[File:Gfpfl50.png|thumb|900px|center|'''Figure 2''': Stochastic simulation of GFP steady state for an Acetaldehyde concentration of 46 μM.]] | ||
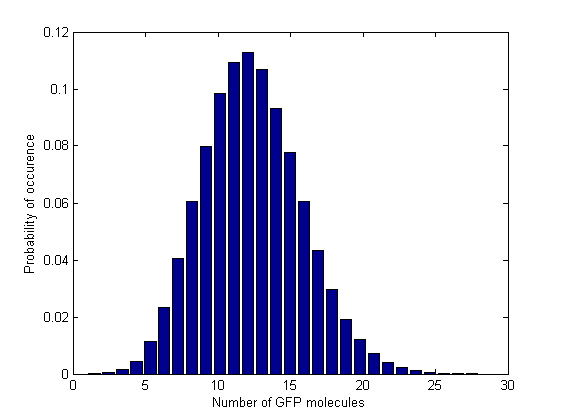
| - | Next, in order to see how the values are distributed and whether there are multiple steady states, we plotted the normalized histograms for the 5 data sets. We used 150 bins for plotting the histograms for the 3 intermediate Acetaldehyde values and 28 | + | Next, in order to see how the values are distributed and whether there are multiple steady states, we plotted the normalized histograms for the 5 data sets. We used 150 bins for plotting the histograms for the 3 intermediate Acetaldehyde values and 28 and 61 bins for the first and last Acetaldehyde value, respectively. In these last 2 cases we had to reduce the number of bins because the range of the GFP molecule values was narrower. |
{| border="0" width="100%" | {| border="0" width="100%" | ||
| Line 57: | Line 58: | ||
= Analysis of Results = | = Analysis of Results = | ||
| - | From the time course plot (Figure 2) we can already see that the values always fluctuate around one | + | From the time course plot (Figure 2) we can already see that the values always fluctuate around one mean value which leads us to believe that the system is stable. Since the numbers of GFP molecules do not jump between two or more distinct values we can assume that the system is not bistable. The plot alone however does not constitute conclusive evidence, so for this reason we generated and analyzed the distributions of GFP values. |
| - | + | <br> <br> | |
| - | All of the 5 distributions have a Gaussian shape, which means that the GFP values cluster around one mean value. | + | All of the 5 distributions have a Gaussian-like shape, which means that the GFP values cluster around one mean value. The distributions are relatively narrow, which means there are no large fluctuations and there are unimodal, which corresponds to a having no multiple stead states in the deterministic regime. |
{|style="margin: 1em auto 1em auto; width: 80%;" class="wikitable sortable" | {|style="margin: 1em auto 1em auto; width: 80%;" class="wikitable sortable" | ||
| Line 68: | Line 69: | ||
!GFP standard deviation (no. of molecules) | !GFP standard deviation (no. of molecules) | ||
!GFP standard deviation (μM) | !GFP standard deviation (μM) | ||
| + | !GFP relative standard deviation (%) | ||
|- | |- | ||
|0 μM | |0 μM | ||
| Line 75: | Line 77: | ||
|3.5473 | |3.5473 | ||
|0.0029 μM | |0.0029 μM | ||
| + | |28.86 % | ||
|- | |- | ||
|25 μM | |25 μM | ||
| Line 82: | Line 85: | ||
|544.6184 | |544.6184 | ||
|0.4522 μM | |0.4522 μM | ||
| + | |27.86 % | ||
|- | |- | ||
|46 μM | |46 μM | ||
| Line 89: | Line 93: | ||
|669.5291 | |669.5291 | ||
|0.5559 μM | |0.5559 μM | ||
| + | |2.85 % | ||
|- | |- | ||
|100 μM | |100 μM | ||
| Line 96: | Line 101: | ||
|243.6979 | |243.6979 | ||
|0.2023 μM | |0.2023 μM | ||
| + | |8.17 % | ||
|- | |- | ||
|300 μM | |300 μM | ||
| Line 103: | Line 109: | ||
|7.1426 | |7.1426 | ||
|0.0059 μM | |0.0059 μM | ||
| + | |17.85 % | ||
|} | |} | ||
| + | In the table above we can see that the mean values of the distributions of GFP molecule numbers (in concentration) obtained from the stochastic simulations are very similar to the deterministic ones obtained previously by simulating the system with an ODE solver. This confirms once again the fact that the deterministic steady state corresponds to the stochastic one, thus it sees that we do not have bifurcations.. | ||
| + | <br> <br> | ||
| + | Analyzing the relative standard deviations (RSD), we notice that the highest value was obtained for an input concentration of acetaldehyde equal to 0 μM. This is due to the fact that in this case GFP is repressed, so there is only leaky GFP expression. As the GFP output is on the order of a few up to tens of molecules, the ratio between the value of the mean and the amplitude of the fluctuations is much higher than the absolute value of the fluctuations. | ||
| + | <br> <br> | ||
| + | The lowest RSD corresponds to the acetaldehyde concentration that gives the GFP peak (46 μM). This is in accordance to the central limit theorem, since for higher values of the mean the relative value of the fluctuations decreases. We can notice that for 46 μM of acetaldehyde the standard deviation is on the same order of magnitude as for 25 and 100 μM of acetaldehyde, however the RSD is much smaller for the peak value. | ||
| + | <br> <br> | ||
| + | The RSD is higher in the region where the GFP increases compared the region where it decreases despite the fact the value of the mean is comparable. This can be explained by taking into account the steepness of the slope which is higher for 25 than for 100 μM of acetaldehyde. On the left side of the peak the GFP value changes more quickly than on the right side, meaning that it is more prone to larger fluctuations. | ||
{{:Team:ETH Zurich/Templates/SectionEnd}} | {{:Team:ETH Zurich/Templates/SectionEnd}} | ||
{{:Team:ETH Zurich/Templates/HeaderNewEnd}} | {{:Team:ETH Zurich/Templates/HeaderNewEnd}} | ||
Latest revision as of 22:27, 28 October 2011
Stochastic Analysis
Besides the parameter space search, we performed another type of analysis in order to verify that our system is robust and that it is monostable (i.e. it has only one steady state). We were especially interested in the GFP band, whether it is always present and whether the amount of GFP produced in the cells for different concentrations of Acetaldehyde has large fluctuations. Because gene expression is an intrinsically stochastic process, we performed stochastic simulations to see how our system reacts to noise and how it responds to perturbations.
The following results show that our system is indeed robust to noise and it does not have bifurcations.
Method
For the stochastic simulations we used the [http://magnet.systemsbiology.net/software/Dizzy/ Dizzy] software, to which we gave as an input an SBML file with the description of our system. Moving from deterministic to stochastic simulations we had to change several things in the SBML file. Firstly, we exported the SBML file to a CMDL format.Next, we converted the species values as well as the production rates and repression coefficients from concentrations (in μM) to number of molecules. Since our initial system was described in terms of ODEs, we also had to change this by separating the system into distinct reaction channels (i.e. separate degradation from activation/repression) and specifying the reaction rates.
With the new description of the system, we could start the simulations. For analyzing the robustness of the system, we chose 5 strategic Acetaldehyde concentrations (see Figure 1), and for each of them we performed stochastic simulations. We selected the following Acetaldehyde concentrations:
- 0 μM (0 molecules). At this concentration the GFP output should approach 0 μM.
- 25 μM (30110 molecules). At this concentration GFP rises quickly, so it should be very sensitive to noise.
- 46 μM (55402 molecules). This is the concentration that gives the peak GFP value.
- 100 μM (120440 molecules). At this concentration GFP is decreasing, so it should be sensitive to noise.
- 300 μM (361320 molecules). At this concentration the GFP output should again approach 0 μM.
In order to be sure that we are indeed simulating the time course of the "stochastic steady state", and that we are not in the transient regime, we implemented the following approach:
- We ran a deterministic simulation for 5000 minutes (~ 83 hours) to get to the deterministic steady state. We took over the concentration values for the last time point as new initial conditions for the next simulation.
- We ran a stochastic simulation for 10000 minutes (~ 7 days), to make sure that we are somewhere around the “stochastic steady state”. Once again we took over the concentration values for the last time point as new initial conditions for the next simulation.
- We ran a long stochastic simulation for 100000 minutes (~ 70 days) storing the molecule numbers of the species every minute.
For the stochastic simulations we used the "Gillespie-direct" option, since this gives an exact solution, compared to the other solvers which only approximate the solution.
Simulations
After we obtained the samples with Dizzy, we loaded the data in Matlab to analyze it. To get an initial feeling of how the system behaves in the stochastic regime, we plotted the GFP molecule numbers as function of time. In Figure 2 we can see that for the peak of the band (Acetaldehyde = 46 μM), GFP values fluctuate around a mean value which is about 23500 molecules.
Next, in order to see how the values are distributed and whether there are multiple steady states, we plotted the normalized histograms for the 5 data sets. We used 150 bins for plotting the histograms for the 3 intermediate Acetaldehyde values and 28 and 61 bins for the first and last Acetaldehyde value, respectively. In these last 2 cases we had to reduce the number of bins because the range of the GFP molecule values was narrower.
|
| |
Analysis of Results
From the time course plot (Figure 2) we can already see that the values always fluctuate around one mean value which leads us to believe that the system is stable. Since the numbers of GFP molecules do not jump between two or more distinct values we can assume that the system is not bistable. The plot alone however does not constitute conclusive evidence, so for this reason we generated and analyzed the distributions of GFP values.
All of the 5 distributions have a Gaussian-like shape, which means that the GFP values cluster around one mean value. The distributions are relatively narrow, which means there are no large fluctuations and there are unimodal, which corresponds to a having no multiple stead states in the deterministic regime.
| Acetaldehyde concentration | GFP mean (no. of molecules) | GFP mean (μM) | Deterministic GFP value (μM) | GFP standard deviation (no. of molecules) | GFP standard deviation (μM) | GFP relative standard deviation (%) |
|---|---|---|---|---|---|---|
| 0 μM | 12.2903 | 0.0102 μM | 0.01 μM | 3.5473 | 0.0029 μM | 28.86 % |
| 25 μM | 1954.4 | 1.6227 μM | 1.7157 μM | 544.6184 | 0.4522 μM | 27.86 % |
| 46 μM | 23491 | 19.5046 μM | 19.6046 μM | 669.5291 | 0.5559 μM | 2.85 % |
| 100 μM | 2981.7 | 2.4757 μM | 2.4830 μM | 243.6979 | 0.2023 μM | 8.17 % |
| 300 μM | 40.0056 | 0.0332 μM | 0.0332 μM | 7.1426 | 0.0059 μM | 17.85 % |
In the table above we can see that the mean values of the distributions of GFP molecule numbers (in concentration) obtained from the stochastic simulations are very similar to the deterministic ones obtained previously by simulating the system with an ODE solver. This confirms once again the fact that the deterministic steady state corresponds to the stochastic one, thus it sees that we do not have bifurcations..
Analyzing the relative standard deviations (RSD), we notice that the highest value was obtained for an input concentration of acetaldehyde equal to 0 μM. This is due to the fact that in this case GFP is repressed, so there is only leaky GFP expression. As the GFP output is on the order of a few up to tens of molecules, the ratio between the value of the mean and the amplitude of the fluctuations is much higher than the absolute value of the fluctuations.
The lowest RSD corresponds to the acetaldehyde concentration that gives the GFP peak (46 μM). This is in accordance to the central limit theorem, since for higher values of the mean the relative value of the fluctuations decreases. We can notice that for 46 μM of acetaldehyde the standard deviation is on the same order of magnitude as for 25 and 100 μM of acetaldehyde, however the RSD is much smaller for the peak value.
The RSD is higher in the region where the GFP increases compared the region where it decreases despite the fact the value of the mean is comparable. This can be explained by taking into account the steepness of the slope which is higher for 25 than for 100 μM of acetaldehyde. On the left side of the peak the GFP value changes more quickly than on the right side, meaning that it is more prone to larger fluctuations.
 "
"