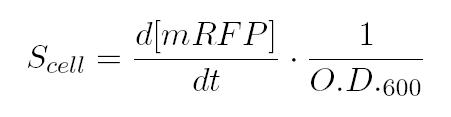|
|
| (96 intermediate revisions not shown) |
| Line 2: |
Line 2: |
| | | | |
| | <html> | | <html> |
| | + | |
| | <h2 class="art-postheader">Modelling</h2> | | <h2 class="art-postheader">Modelling</h2> |
| | <div class="cleared"></div> | | <div class="cleared"></div> |
| | <div class="art-postcontent"> | | <div class="art-postcontent"> |
| | + | |
| | <p><a name="indice"/> </p> | | <p><a name="indice"/> </p> |
| - | <table id="toc" class="toc"> | + | <table id="toc" class="toc"><tr><td><div id="toctitle"><h2>Contents</h2></div> |
| - | <tr>
| + | <ul> |
| - | <td><div id="toctitle">
| + | <li class="toclevel-1"><a href="#Mathematical_modelling_page"><span class="tocnumber"></span> <span class="toctext">Mathematical modelling: introduction</span></a> |
| - | <h2>Contents</h2>
| + | <ul> <br> |
| - | </div>
| + | <li class="toclevel-2"><a href="#The importance of the mathematical model"><span class="tocnumber">1</span> <span class="toctext">The importance of mathematical modelling</span></a></li> |
| - | <ul>
| + | <li class="toclevel-2"><a href="#Equations_for_gene_networks"><span class="tocnumber">2</span> <span class="toctext">Equations for gene networks</span></a></li> |
| - | <li class="toclevel-1"><a href="#Mathematical_modelling_page"><span class="tocnumber"></span> <span class="toctext">Mathematical modelling: introduction</span></a>
| + | <ul> |
| - | <ul>
| + | <li class="toclevel-3"><a href="#Hypothesis"><span class="tocnumber">2.1</span> <span class="toctext">Hypotheses</span></a></li> |
| - | <br>
| + | <li class="toclevel-3"><a href="#Equations_1_and_2"><span class="tocnumber">2.2</span> <span class="toctext">Equations (1) and (2)</span></a></li> |
| - | <li class="toclevel-2"><a href="#The importance of the mathematical model"><span class="tocnumber">1</span> <span class="toctext">The importance of mathematical modelling</span></a></li>
| + | <li class="toclevel-3"><a href="#Equation_3"><span class="tocnumber">2.3</span> <span class="toctext">Equation (3)</span></a></li> |
| - | <li class="toclevel-2"><a href="#Equations_for_gene_networks"><span class="tocnumber">2</span> <span class="toctext">Equations for gene networks</span></a></li>
| + | <li class="toclevel-3"><a href="#Equation_4"><span class="tocnumber">2.4</span> <span class="toctext">Equation (4)</span></a></li> |
| - | <ul>
| + | </ul> |
| - | <li class="toclevel-3"><a href="#Hypothesis"><span class="tocnumber">2.1</span> <span class="toctext">Hypotheses</span></a></li>
| + | |
| - | <li class="toclevel-3"><a href="#Equations_1_and_2"><span class="tocnumber">2.2</span> <span class="toctext">Equations (1) and (2)</span></a></li>
| + | <li class="toclevel-2"><a href="#Table_of_parameters"><span class="tocnumber">3</span> <span class="toctext">Table of parameters</span></a></li> |
| - | <li class="toclevel-3"><a href="#Equation_3"><span class="tocnumber">2.3</span> <span class="toctext">Equation (3)</span></a></li>
| + | <ul> |
| - | <li class="toclevel-3"><a href="#Equation_4"><span class="tocnumber">2.4</span> <span class="toctext">Equation (4)</span></a></li>
| + | <li class="toclevel-3"><a href="#CV"><span class="tocnumber">3</span> <span class="toctext">Table of parameter CV</span></a></li> |
| - | </ul>
| + | </ul> |
| - | <li class="toclevel-2"><a href="#Table_of_parameters"><span class="tocnumber">3</span> <span class="toctext">Table of parameters</span></a></li>
| + | |
| - | <ul>
| + | <li class="toclevel-2"><a href="#Parameter_estimation"><span class="tocnumber">4</span> <span class="toctext">Parameter estimation</span></a></li> |
| - | <li class="toclevel-3"><a href="#CV"><span class="tocnumber">3</span> <span class="toctext">Table of parameter CV</span></a></li>
| + | <ul> |
| - | </ul>
| + | <li class="toclevel-3"><a href="#Ptet_&_Plux"><span class="tocnumber">4.1</span> <span class="toctext">pTet & pLux</span></a></li> |
| - | <li class="toclevel-2"><a href="#Parameter_estimation"><span class="tocnumber">4</span> <span class="toctext">Parameter estimation</span></a></li>
| + | <li class="toclevel-3"><a href="#introduction_to_T9002"><span class="tocnumber">4.2</span> <span class="toctext">T9002 introduction</span></a></li> |
| - | <ul>
| + | <li class="toclevel-3"><a href="#Enzymes"><span class="tocnumber">4.3</span> <span class="toctext"> AiiA & LuxI</span></a></li> |
| - | <li class="toclevel-3"><a href="#Ptet_&_Plux"><span class="tocnumber">4.1</span> <span class="toctext">pTet & pLux</span></a></li>
| + | <li class="toclevel-3"><a href="#N"><span class="tocnumber">4.4</span> <span class="toctext">N</span></a></li> |
| - | <li class="toclevel-3"><a href="#introduction_to_T9002"><span class="tocnumber">4.2</span> <span class="toctext">T9002 introduction</span></a></li>
| + | <li class="toclevel-3"><a href="#Degradation_rates"><span class="tocnumber">4.5</span> <span class="toctext">Degradation rates</span></a></li></ul> |
| - | <li class="toclevel-3"><a href="#Enzymes"><span class="tocnumber">4.3</span> <span class="toctext"> AiiA & LuxI</span></a></li>
| + | |
| - | <li class="toclevel-3"><a href="#N"><span class="tocnumber">4.4</span> <span class="toctext">N</span></a></li>
| + | |
| - | <li class="toclevel-3"><a href="#Degradation_rates"><span class="tocnumber">4.5</span> <span class="toctext">Degradation rates</span></a></li>
| + | <li class="toclevel-2"><a href="#Simulations"><span class="tocnumber">5</span> <span class="toctext">Simulations</span></a></li> <li class="toclevel-1"><a href="#Sensitivity_Analysis"><span class="tocnumber">6</span> <span class="toctext">Sensitivity Analysis of the steady state of enzyme expression in exponential phase</span></a></li> |
| - | </ul>
| + | <ul> |
| - | <li class="toclevel-2"><a href="#Simulations"><span class="tocnumber">5</span> <span class="toctext">Simulations</span></a></li>
| + | <li class="toclevel-2"><a href="#Steady state of enzyme expression"><span class="tocnumber">6.1</span> <span class="toctext">Steady state of enzyme expression</span></a></li> |
| - | <li class="toclevel-1"><a href="#Sensitivity_Analysis"><span class="tocnumber">6</span> <span class="toctext">Sensitivity Analysis of the steady state of enzyme expression in exponential phase</span></a></li>
| + | <li class="toclevel-2"><a href="#Sensitivity analysis"><span class="tocnumber">6.2</span> <span class="toctext">Sensitivity analysis</span></a></li> |
| - | <ul>
| + | </ul> |
| - | <li class="toclevel-2"><a href="#Steady state of enzyme expression"><span class="tocnumber">6.1</span> <span class="toctext">Steady state of enzyme expression</span></a></li>
| + | <li class="toclevel-1"><a href="#References"><span class="tocnumber">7</span> <span class="toctext">References</span></a></li> |
| - | <li class="toclevel-2"><a href="#Sensitivity analysis"><span class="tocnumber">6.2</span> <span class="toctext">Sensitivity analysis</span></a></li>
| + | </ul> |
| - | </ul>
| + | </li> |
| - | <li class="toclevel-1"><a href="#References"><span class="tocnumber">7</span> <span class="toctext">References</span></a></li>
| + | </ul> |
| - | </ul>
| + | </li> |
| - | </li>
| + | </ul> |
| - | </ul>
| + | </td></tr></table> |
| - | </li>
| + | <script>if (window.showTocToggle) { var tocShowText = "show"; var tocHideText = "hide"; showTocToggle(); } </script> |
| - | </ul></td>
| + | <br><br> |
| - | </tr>
| + | |
| - | </table> | + | |
| - | <br> | + | |
| - | <br> | + | |
| | <div class="listcircle"> | | <div class="listcircle"> |
| - | <a name="Mathematical_modelling_page"></a> | + | |
| - | <h1><span class="mw-headline"> <b>Mathematical modelling: introduction</b> </span></h1> | + | <a name="Mathematical_modelling_page"></a><h1><span class="mw-headline"> <b>Mathematical modelling: introduction</b> </span></h1> |
| - | <div style='text-align:justify'> | + | <div style='text-align:justify'><p>Mathematical modelling plays a central role in Synthetic Biology, due to its ability to serve as a crucial link between the concept and realization of a biological circuit: what we propose in this page is a mathematical modelling approach to the entire project, which has proven extremely useful before and after the "wet lab" activities.</p> |
| - | <p>Mathematical modelling plays a central role in Synthetic Biology, due to its ability to serve as a crucial link between the concept and realization of a biological circuit: what we propose in this page is a mathematical modelling approach to the entire project, which has proven extremely useful before and after the "wet lab" activities.</p>
| + | |
| - | <p>Thus, immediately at the beginning, when there was little knowledge, a mathematical model based on a system of differential equations was derived and implemented using a set of reasonable values of model parameters, to validate the feasibility of the project. Once this became clear, starting from the characterization of each simple subpart created in the wet lab, some of the parameters of the mathematical model were estimated thanks to several ad-hoc experiments we performed within the iGEM project (others were derived from literature) and they were used to predict the final behaviour of the whole engineered closed-loop circuit. This approach is consistent with the typical one adopted for the analysis and synthesis of a biological circuit, as exemplified by <a href="#Pasotti"><i><b>Pasotti L</b> et al. 2011.</i></a></p>
| + | <p>Thus, immediately at the beginning, when there was little knowledge, a mathematical model based on a system of differential equations was derived and implemented using a set of reasonable values of model parameters, to validate the feasibility of the project. Once this became clear, starting from the characterization of each simple subpart created in the wet lab, some of the parameters of the mathematical model were estimated thanks to several ad-hoc experiments we performed within the iGEM project (others were derived from literature) and they were used to predict the final behaviour of the whole engineered closed-loop circuit. This approach is consistent with the typical one adopted for the analysis and synthesis of a biological circuit, as exemplified by <a href="#Pasotti"><i><b>Pasotti L</b> et al. 2011.</i></a></p> |
| - | <p>After a brief overview on the importance of the mathematical modelling approach, we deeply analyze the system of equations, underlining the role and function of the parameters involved.</p>
| + | |
| - | <p>Experimental procedures for parameter estimation are discussed and, finally, a different type of circuit is presented. <font color="red">Simulations were performed, using <em>ODEs</em> with MATLAB and used to explain the difference between a closed-loop control system model and an open one.</font>
| + | <p>After a brief overview on the importance of the mathematical modelling approach, we deeply analyze the system of equations, underlining the role and function of the parameters involved.</p> |
| - | </div> | + | <p>Experimental procedures for parameter estimation are discussed and simulations performed, using <em>ODEs</em> with MATLAB. </div></p> |
| - | </p> | + | |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| - | <br> | + | <br> |
| - | <a name="The importance of the mathematical model"></a> | + | |
| - | <h2> <span class="mw-headline"> <b>The importance of mathematical modelling</b> </span></h2> | + | |
| - | <div style='text-align:justify'> | + | <a name="The importance of the mathematical model"></a><h2> <span class="mw-headline"> <b>The importance of mathematical modelling</b> </span></h2> |
| - | <p>Mathematical modelling reveals fundamental in the challenge of understanding and engineering complex biological systems. Indeed, these are characterized by a high degree of interconnection among the single constituent parts, requiring a comprehensive analysis of their behavior through mathematical formalisms and computational tools.</p>
| + | <div style='text-align:justify'><p>Mathematical modelling reveals fundamental in the challenge of understanding and engineering complex biological systems. Indeed, these are characterized by a high degree of interconnection among the single constituent parts, requiring a comprehensive analysis of their behavior through mathematical formalisms and computational tools.</p> |
| - | <div>Synthetically, we can identify two major roles concerning mathematical models:</div>
| + | <div>Synthetically, we can identify two major roles concerning mathematical models:</div> |
| - | <ul>
| + | |
| - | <p>
| + | <ul> |
| - | <li><b>Simulation</b>: mathematical models allow to analyse complex system dynamics and to reveal the relationships between the involved variables, starting from the knowledge of the single subparts behavior and from simple hypotheses of their interconnection. <a href="#Endler">(<i><b>Endler L</b> et al. 2009</i>)</a></li>
| + | |
| - | </p>
| + | |
| - | <p>
| + | |
| - | <li><b>Knowledge elicitation</b>: mathematical models summarize into a small set of parameters the results of several experiments (parameter identification), allowing a robust comparison among different experimental conditions and providing an efficient way to synthesize knowledge about biological processes. Then, through the simulation process, they make possible the re-usability of the knowledge coming from different experiments, engineering complex systems from the composition of its constituent subparts under appropriate experimental/environmental conditions <a href="#Braun">(<i><b>Braun D</b> et al. 2005</a>;<a href="#Canton"> <b>Canton B</b> et al 2008</a>)</font>.</li>
| + | <p><li><b>Simulation</b>: mathematical models allow to analyse complex system dynamics and to reveal the relationships between the involved variables, starting from the knowledge of the single subparts behavior and from simple hypotheses of their interconnection. <a href="#Endler">(<i><b>Endler L</b> et al. 2009</i>)</a></li></p> |
| - | </p>
| + | |
| - | </ul>
| + | <p><li><b>Knowledge elicitation</b>: mathematical models summarize into a small set of parameters the results of several experiments (parameter identification), allowing a robust comparison among different experimental conditions and providing an efficient way to synthesize knowledge about biological processes. Then, through the simulation process, they make possible the re-usability of the knowledge coming from different experiments, engineering complex systems from the composition of its constituent subparts under appropriate experimental/environmental conditions <a href="#Braun">(<i><b>Braun D</b> et al. 2005</a>;<a href="#Canton"> <b>Canton B</b> et al 2008</a></i>)</font>.</li> |
| | + | </p> |
| | + | |
| | + | </ul> |
| | </div> | | </div> |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| - | <a name="Equations_for_gene_networks"></a> | + | |
| - | <h2> <span class="mw-headline"> <b>Equations for gene networks</b> </span></h2> | + | |
| | + | |
| | + | <a name="Equations_for_gene_networks"></a><h2> <span class="mw-headline"> <b>Equations for gene networks</b> </span></h2> |
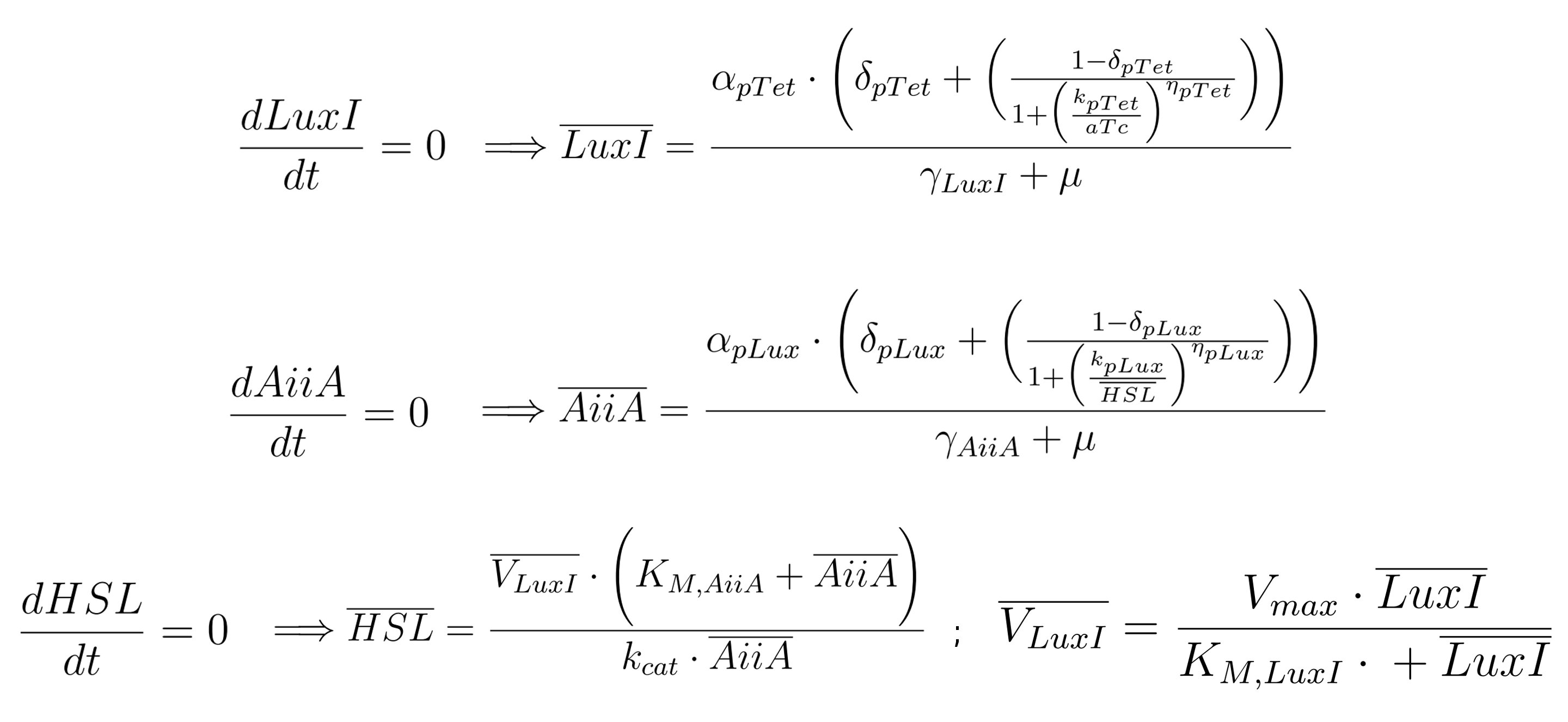
| | <p>Below is provided the system of equations of our mathematical model. </p> | | <p>Below is provided the system of equations of our mathematical model. </p> |
| - | <center> | + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/4/43/Model_new.jpg" class="thumbimage" height="55%" width="80%">
| + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"> |
| - | </center> | + | <a href="https://static.igem.org/mediawiki/2011/4/43/Model_new.jpg"> |
| | + | <img alt="" src="https://static.igem.org/mediawiki/2011/4/43/Model_new.jpg" class="thumbimage" height="55%" width="80%"></a></div></div> |
| | <br> | | <br> |
| - | <center> | + | <table align='center' width='100%'> |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/5/5e/Circuito_finale.jpg" class="thumbimage" width="87%">
| + | <tr> |
| - | </center> | + | <td> |
| - | <center> | + | <div style='text-align:center'><div class="thumbinner" style="width:100%;"><img alt="" src="https://static.igem.org/mediawiki/2011/5/5e/Circuito_finale.jpg" class="thumbimage" width="87%"></a></div></div> |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/c/c7/QS_system_synthetic_circuit.png" class="thumbimage" width="85%">
| + | </td> |
| - | </center> | + | </tr> |
| | + | </table> |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><img alt="" src="https://static.igem.org/mediawiki/2011/c/c7/QS_system_synthetic_circuit.png" class="thumbimage" width="85%"></a></div></div> |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | + | <div style='text-align:center; font-size: 12px; font-style:italic; margin-top=50px; padding-top=50px;'>Schematic description of Ctrl+E system behavior</div> |
| | <br> | | <br> |
| - | <a name="Hypothesis"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Hypotheses of the model</b> </span></h4> | + | |
| | + | |
| | + | <a name="Hypothesis"></a><h4> <span class="mw-headline"> <b>Hypotheses of the model</b> </span></h4> |
| | <table class="data"> | | <table class="data"> |
| - | <tr>
| + | <tr> |
| - | <td><div style='text-align:justify'> <em> <b>HP<sub>1</sub></b>: in equation (2) only HSL is considered as inducer, instead of the complex LuxR-HSL.
| + | <td> |
| - | This is motivated by the fact that our final device offers a constitutive LuxR production due to the upstream constitutive promoter Pλ. Assuming LuxR is abundant in the cytoplasm, we can understand this simplification of attributing pLux promoter induction only by HSL. <br>
| + | <div style='text-align:justify'> |
| - | <br>
| + | <em> |
| - | <b>HP<sub>2</sub></b>: in system equation, LuxI and AiiA amounts are expressed per cell. For this reason, the whole equation (3), except for the
| + | <b>HP<sub>1</sub></b>: in equation (2) only HSL is considered as inducer, instead of the complex LuxR-HSL. |
| - | term of intrinsic degradation of HSL, is multiplied by the number of cells N, due to the property of the lactone to diffuse freely inside/outside bacteria. <br>
| + | This is motivated by the fact that our final device offers a constitutive LuxR production due to the upstream constitutive promoter Pλ. Assuming LuxR is abundant in the cytoplasm, we can understand this simplification of attributing pLux promoter induction only by HSL. |
| - | <br>
| + | <br> |
| - | <b>HP<sub>3</sub></b>: as regards promoters pTet and pLux, we assume their strengths (measured in PoPs), due to a given concentration of inducer (aTc and HSL for Ptet and Plux respectively), to be
| + | <br> |
| - | independent from the gene downstream.
| + | <b>HP<sub>2</sub></b>: in system equation, LuxI and AiiA amounts are expressed per cell. For this reason, the whole equation (3), except for the |
| - | In other words, in our hypothesis, if the mRFP coding region is substituted with a region coding for another gene (in our case, AiiA or LuxI), we would obtain the same synthesis rate:
| + | term of intrinsic degradation of HSL, is multiplied by the number of cells N, due to the property of the lactone to diffuse freely inside/outside bacteria. |
| - | this is the reason why the strength of the complex promoter-RBS is expressed in Arbitrary Units [AUr]. <br>
| + | <br> |
| - | <br>
| + | <br> |
| - | <b>HP<sub>4</sub></b>: considering the exponential growth, the enzymes AiiA and LuxI concentration is supposed to be constant, because their production is equally compensated by dilution. </em> </div></td>
| + | <b>HP<sub>3</sub></b>: as regards promoters pTet and pLux, we assume their strengths (measured in PoPs), due to a given concentration of inducer (aTc and HSL for Ptet and Plux respectively), to be |
| - | </tr>
| + | independent from the gene downstream. |
| | + | In other words, in our hypothesis, if the mRFP coding region is substituted with a region coding for another gene (in our case, AiiA or LuxI), we would obtain the same synthesis rate: |
| | + | this is the reason why the strength of the complex promoter-RBS is expressed in Arbitrary Units [AUr]. |
| | + | <br> |
| | + | <br> |
| | + | <b>HP<sub>4</sub></b>: considering the exponential growth, the enzymes AiiA and LuxI concentration is supposed to be constant, because their production is equally compensated by dilution. |
| | + | </em> |
| | + | </div> |
| | + | </td> |
| | + | </tr> |
| | </table> | | </table> |
| | <br> | | <br> |
| Line 116: |
Line 134: |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <a name="Equations_1_and_2"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Equations (1) and (2)</b> </span></h4> | + | <a name="Equations_1_and_2"></a><h4> <span class="mw-headline"> <b>Equations (1) and (2)</b> </span></h4> |
| - | <div style='text-align:justify'> | + | <div style='text-align:justify'><p>Equations (1) and (2) have identical structure, differing only in the parameters involved. They represent the synthesis, degradation and dilution of both the enzymes in the circuit, LuxI and AiiA, respectively in the first and second equation: in each of them both transcription and translation processes have been condensed. The mathematical formulation is analogous to the one used by <a href="#Pasotti"><i><b>Pasotti L</b> et al. 2011</i></a>, Suppl. Inf., even if we do not take LuxR-HSL complex formation into account, as explained below.</p> |
| - | <p>Equations (1) and (2) have identical structure, differing only in the parameters involved. They represent the synthesis, degradation and diluition of both the enzymes in the circuit, LuxI and AiiA, respectively in the first and second equation: in each of them both transcription and translation processes have been condensed. The mathematical formulation is analogous to the one used by <a href="#Pasotti"><i><b>Pasotti L</b> et al. 2011</i></a>, Suppl. Inf., even if we do not take LuxR-HSL complex formation into account, as explained below.</p>
| + | <p>These equations are composed of 2 parts:</p> |
| - | <p>These equations are composed of 2 parts:</p>
| + | <ol> |
| - | <ol>
| + | <li>The first term describes, through Hill's equation, the synthesis rate of the protein of interest (either LuxI or AiiA) depending on the concentration of the inducer (anhydrotetracicline -aTc- or HSL respectively), responsible for the activation of the regulatory element composed of promoter and RBS. In the parameter table (see below), α refers to the maximum activation of the promoter, while δ stands for its leakage activity (this means that the promoter is slightly active even if there is no induction). In particular, in equation (1), the almost entire inhibition of pTet promoter is given by the constitutive production of TetR by our MGZ1 strain. In equation (2), pLux is almost inactive in the absence of the complex LuxR-HSL. Furthermore, in both equations k stands for the dissociation constant of the promoter from the inducer (respectively aTc and HSL in eq. 1 and 2), while η is the cooperativity constant.</p> |
| - | <li>The first term describes, through Hill's equation, the synthesis rate of the protein of interest (either LuxI or AiiA) depending on the concentration of the inducer (anhydrotetracicline -aTc- or HSL respectively), responsible for the activation of the regulatory element composed of promoter and RBS. In the parameter table (see below), α refers to the maximum activation of the promoter, while δ stands for its leakage activity (this means that the promoter is slightly active even if there is no induction). In particular, in equation (1), the almost entire inhibition of pTet promoter is given by the constitutive production of TetR by our MGZ1 strain. In equation (2), pLux is almost inactive in the absence of the complex LuxR-HSL. Furthermore, in both equations k stands for the dissociation constant of the promoter from the inducer (respectively aTc and HSL in eq. 1 and 2), while η is the cooperativity constant.
| + | <p><li>The second term in equations (1) and (2) is in turn composed of 2 parts. The former one (<em>γ</em>*LuxI or <em>γ</em>*AiiA respectively) describes, with an exponential decay, the degradation rate per cell of the protein. The latter (μ*(Nmax-N)/Nmax)*LuxI or μ*(Nmax-N)/Nmax)*AiiA, respectively) takes into account the dilution factor against cell growth which is related to the cell replication process.</p> |
| - | </p>
| + | </ol> |
| - | <p>
| + | |
| - | <li>The second term in equations (1) and (2) is in turn composed of 2 parts. The former one (<em>γ</em>*LuxI or <em>γ</em>*AiiA respectively) describes, with an exponential decay, the degradation rate per cell of the protein. The latter (μ*(Nmax-N)/Nmax)*LuxI or μ*(Nmax-N)/Nmax)*AiiA, respectively) takes into account the dilution factor against cell growth which is related to the cell replication process.
| + | |
| - | </p>
| + | |
| - | </ol>
| + | |
| | </div> | | </div> |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| - | <a name="Equation_3"></a>
| |
| - | <h4> <span class="mw-headline"> <b>Equation (3)</b> </span></h4>
| |
| - | <div style='text-align:justify'>
| |
| - | <p>Here the kinetics of HSL is modeled, through enzymatic reactions either related to the production or the degradation of HSL. This equation is composed of 3 parts: </p>
| |
| - | <ol>
| |
| - | <p>
| |
| - | <li> The first term represents the production of HSL due to LuxI expression. We modeled this process with a saturation curve in which V<sub>max</sub> is the HSL maximum transcription rate, while k<sub>M,LuxI</sub> is LuxI dependent half-saturation constant.
| |
| - | </p>
| |
| - | <p>
| |
| - | <li> The second term represents the degradation of HSL due to the AiiA expression. Similarly to LuxI, k<sub>cat</sub> represents the maximum degradation per unit of HSL concentration, while k<sub>M,AiiA</sub> is the concentration at which AiiA dependent HSL degradation rate is (k<sub>cat</sub>*HSL)/2. The formalism is similar to that found in the Supplementary Information of <a href="#Danino"><i><b>Danino T</b> et al 2010.</i></a></font>
| |
| - | </p>
| |
| - | <p>
| |
| - | <li> The third term (γ<sub>HSL</sub>*HSL) is similar to the corresponding ones present in the first two equations and describes the intrinsic protein degradation.
| |
| | | | |
| - | <div align="right"><small><a href="#indice">^top</a></small></div> | + | |
| - | </p> | + | |
| | + | <a name="Equation_3"></a><h4> <span class="mw-headline"> <b>Equation (3)</b> </span></h4> |
| | + | <div style='text-align:justify'><p>Here the kinetics of HSL is modeled, through enzymatic reactions either related to the production or the degradation of HSL. This equation is composed of 3 parts: </p> |
| | + | <ol> |
| | + | <p><li> The first term represents the production of HSL due to LuxI expression. We modeled this process with a saturation curve in which V<sub>max</sub> is the HSL maximum transcription rate, while k<sub>M,LuxI</sub> is LuxI dependent half-saturation constant.</p> |
| | + | <p><li> The second term represents the degradation of HSL due to the AiiA expression. Similarly to LuxI, k<sub>cat</sub> represents the maximum degradation per unit of HSL concentration, while k<sub>M,AiiA</sub> is the concentration at which AiiA dependent HSL degradation rate is (k<sub>cat</sub>*HSL)/2. The formalism is similar to that found in the Supplementary Information of <a href="#Danino"><i><b>Danino T</b> et al 2010.</i></a></font></p> |
| | + | <p><li> The third term (γ<sub>HSL</sub>*HSL) is similar to the corresponding ones present in the first two equations and describes the intrinsic protein degradation.</div> |
| | + | <div align="right"><small><a href="#indice">^top</a></small></div></p> |
| | <br> | | <br> |
| - | <a name="Equation_4"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Equation (4)</b> </span></h4> | + | |
| | + | <a name="Equation_4"></a><h4> <span class="mw-headline"> <b>Equation (4)</b> </span></h4> |
| | <div style='text-align:justify'>This is the typical cells growth equation, depending on the rate μ and the maximum number N<sub>max</sub> of cells per well reachable <a href="#Pasotti">(<i><b>Pasotti L</b> et al. 2009</i>).</a></div> | | <div style='text-align:justify'>This is the typical cells growth equation, depending on the rate μ and the maximum number N<sub>max</sub> of cells per well reachable <a href="#Pasotti">(<i><b>Pasotti L</b> et al. 2009</i>).</a></div> |
| - | <div align="right"><br> | + | <div align="right"><br><small><a href="#indice">^top</a></small></div> |
| - | <small><a href="#indice">^top</a></small></div>
| + | <br><br> |
| - | <br> | + | |
| - | <br> | + | |
| - | <a name="Table_of_parameters"></a> | + | <a name="Table_of_parameters"></a><h2> <span class="mw-headline"> <b>Table of parameters and species</b> </span></h2> |
| - | <h2> <span class="mw-headline"> <b>Table of parameters and species</b> </span></h2> | + | |
| | <br> | | <br> |
| | + | |
| | + | |
| | + | |
| | <center> | | <center> |
| - | <table class="data">
| + | <table class="data"> |
| - | <tr>
| + | |
| - | <td class="row"><b>Parameter & Species</b></td>
| + | |
| - | <td class="row"><b>Description</b></td>
| + | |
| - | <td class="row"><b>Unit of Measurement</b></td>
| + | |
| - | <td class="row"><b>Value</b></td>
| + | |
| - | </tr>
| + | |
| | <tr> | | <tr> |
| | + | <td class="row" width='15%'><b>Parameter & Species</b></td> |
| | + | <td class="row" width='50%'><b>Description</b></td> |
| | + | <td class="row" width='15%'><b>Measurement Unit</b></td> |
| | + | <td class="row" width='20%'><b>Value</b></td> |
| | + | </tr> |
| | + | |
| | + | |
| | + | <tr> |
| | <td class="row">α<sub>p<sub>Tet</sub></sub></td> | | <td class="row">α<sub>p<sub>Tet</sub></sub></td> |
| | <td class="row">maximum transcription rate of pTet (dependent on <a href="#RBS">RBSx</a> efficiency)</td> | | <td class="row">maximum transcription rate of pTet (dependent on <a href="#RBS">RBSx</a> efficiency)</td> |
| | <td class="row">[(AUr/min)/cell]</td> | | <td class="row">[(AUr/min)/cell]</td> |
| - | <td class="row">-</td> | + | <td class="row">230.67 (RBS30)<br> |
| - | </tr>
| + | ND (RBS31)<br> |
| - | <tr>
| + | 55.77 (RBS32)<br> |
| | + | 120 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | |
| | + | <tr> |
| | <td class="row">δ<sub>p<sub>Tet</sub></sub></td> | | <td class="row">δ<sub>p<sub>Tet</sub></sub></td> |
| | <td class="row">leakage factor of promoter pTet basic activity</td> | | <td class="row">leakage factor of promoter pTet basic activity</td> |
| | <td class="row">[-]</td> | | <td class="row">[-]</td> |
| - | <td class="row">-</td> | + | <td class="row">0.028 (RBS30)<br> |
| - | </tr>
| + | ND (RBS31)<br> |
| - | <tr>
| + | 1.53E-11 (RBS32)<br> |
| | + | 0.085 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | <td class="row">η<sub>p<sub>Tet</sub></sub></td> | | <td class="row">η<sub>p<sub>Tet</sub></sub></td> |
| | <td class="row">Hill coefficient of pTet</td> | | <td class="row">Hill coefficient of pTet</td> |
| | <td class="row">[-]</td> | | <td class="row">[-]</td> |
| - | <td class="row">-</td> | + | <td class="row">4.61 (RBS30)<br> |
| - | </tr>
| + | ND (RBS31)<br> |
| - | <tr>
| + | 4.98 (RBS32)<br> |
| | + | 24.85 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | <td class="row">k<sub>p<sub>Tet</sub></sub></td> | | <td class="row">k<sub>p<sub>Tet</sub></sub></td> |
| | <td class="row">dissociation constant of aTc from pTet</td> | | <td class="row">dissociation constant of aTc from pTet</td> |
| | <td class="row">[ng/ml]</td> | | <td class="row">[ng/ml]</td> |
| - | <td class="row">-</td> | + | <td class="row">8.75 (RBS30)<br> |
| - | </tr>
| + | ND (RBS31)<br> |
| - | <tr>
| + | 7.26 (RBS32)<br> |
| | + | 9 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | <td class="row">α<sub>p<sub>Lux</sub></sub></td> | | <td class="row">α<sub>p<sub>Lux</sub></sub></td> |
| | <td class="row">maximum transcription rate of pLux (dependent on <a href="#RBS">RBSx</a> efficiency)</td> | | <td class="row">maximum transcription rate of pLux (dependent on <a href="#RBS">RBSx</a> efficiency)</td> |
| | <td class="row">[(AUr/min)/cell]</td> | | <td class="row">[(AUr/min)/cell]</td> |
| - | <td class="row">-</td> | + | <td class="row">438 (RBS30)<br> |
| - | </tr>
| + | 9.8 (RBS31)<br> |
| - | <tr>
| + | 206 (RBS32)<br> |
| | + | 1105 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | |
| | + | <tr> |
| | <td class="row">δ<sub>p<sub>Lux</sub></sub></td> | | <td class="row">δ<sub>p<sub>Lux</sub></sub></td> |
| | <td class="row">leakage factor of promoter pLux basic activity</td> | | <td class="row">leakage factor of promoter pLux basic activity</td> |
| | <td class="row">[-]</td> | | <td class="row">[-]</td> |
| - | <td class="row">-</td> | + | <td class="row">0.05 (RBS30)<br> |
| - | </tr>
| + | 0.11 (RBS31)<br> |
| - | <tr>
| + | 0 (RBS32)<br> |
| | + | 0.02 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | <td class="row">η<sub>p<sub>Lux</sub></sub></td> | | <td class="row">η<sub>p<sub>Lux</sub></sub></td> |
| | <td class="row">Hill coefficient of pLux</td> | | <td class="row">Hill coefficient of pLux</td> |
| | <td class="row">[-]</td> | | <td class="row">[-]</td> |
| - | <td class="row">-</td> | + | <td class="row">2 (RBS30)<br> |
| - | </tr>
| + | 1.2 (RBS31)<br> |
| - | <tr>
| + | 1.36 (RBS32)<br> |
| | + | 1.33 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | <td class="row">k<sub>p<sub>Lux</sub></sub></td> | | <td class="row">k<sub>p<sub>Lux</sub></sub></td> |
| | <td class="row">dissociation constant of HSL from pLux</td> | | <td class="row">dissociation constant of HSL from pLux</td> |
| | <td class="row">[nM]</td> | | <td class="row">[nM]</td> |
| - | <td class="row">-</td> | + | <td class="row">1.88 (RBS30)<br> |
| - | </tr>
| + | 1.5 (RBS31)<br> |
| - | <tr>
| + | 1.87 (RBS32)<br> |
| - | <td class="row">γ<sub>p<sub>Lux</sub></sub></td> | + | 2.34 (RBS34)</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">γ<sub>LuxI</sub></td> |
| | <td class="row">LuxI constant degradation</td> | | <td class="row">LuxI constant degradation</td> |
| | <td class="row">[1/min]</td> | | <td class="row">[1/min]</td> |
| - | <td class="row">-</td> | + | <td class="row">0.0173</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| | <td class="row">γ<sub>AiiA</sub></td> | | <td class="row">γ<sub>AiiA</sub></td> |
| | <td class="row">AiiA constant degradation</td> | | <td class="row">AiiA constant degradation</td> |
| | <td class="row">[1/min]</td> | | <td class="row">[1/min]</td> |
| - | <td class="row">-</td> | + | <td class="row">0.0173</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">γ<sub>HSL</sub></td> | | <td class="row">γ<sub>HSL</sub></td> |
| | <td class="row">HSL constant degradation</td> | | <td class="row">HSL constant degradation</td> |
| | <td class="row">[1/min]</td> | | <td class="row">[1/min]</td> |
| - | <td class="row">-</td> | + | <td class="row">0 (pH=6)</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">V<sub>max</sub></td> | | <td class="row">V<sub>max</sub></td> |
| - | <td class="row">maximum transcription rate of LuxI</td> | + | <td class="row">maximum transcription rate of LuxI per cell</td> |
| | <td class="row">[nM/(min*cell)]</td> | | <td class="row">[nM/(min*cell)]</td> |
| - | <td class="row">-</td> | + | <td class="row">3.56*10-9</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">k<sub>M,LuxI</sub></td> | | <td class="row">k<sub>M,LuxI</sub></td> |
| | <td class="row">half-saturation constant of LuxI from HSL</td> | | <td class="row">half-saturation constant of LuxI from HSL</td> |
| | <td class="row">[AUr/cell]</td> | | <td class="row">[AUr/cell]</td> |
| - | <td class="row">-</td> | + | <td class="row">6.87*10<sup>3</sup></td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| | <td class="row">k<sub>cat</sub></td> | | <td class="row">k<sub>cat</sub></td> |
| | <td class="row">maximum number of enzymatic reactions catalyzed per minute</td> | | <td class="row">maximum number of enzymatic reactions catalyzed per minute</td> |
| | <td class="row">[1/(min*cell)]</td> | | <td class="row">[1/(min*cell)]</td> |
| - | <td class="row">-</td> | + | <td class="row">ND</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">k<sub>M,AiiA</sub></td> | | <td class="row">k<sub>M,AiiA</sub></td> |
| | <td class="row">half-saturation constant of AiiA from HSL</td> | | <td class="row">half-saturation constant of AiiA from HSL</td> |
| | <td class="row">[AUr/cell]</td> | | <td class="row">[AUr/cell]</td> |
| - | <td class="row">-</td> | + | <td class="row">ND</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">N<sub>max</sub></td> | | <td class="row">N<sub>max</sub></td> |
| | <td class="row">maximum number of bacteria per well</td> | | <td class="row">maximum number of bacteria per well</td> |
| | <td class="row">[cell]</td> | | <td class="row">[cell]</td> |
| - | <td class="row">-</td> | + | <td class="row">1*10<sup>9</sup></td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | |
| | + | <tr> |
| | <td class="row">μ</td> | | <td class="row">μ</td> |
| | <td class="row">rate of bacteria growth</td> | | <td class="row">rate of bacteria growth</td> |
| | <td class="row">[1/min]</td> | | <td class="row">[1/min]</td> |
| - | <td class="row">-</td> | + | <td class="row">0.004925</td> |
| - | </tr>
| + | </tr> |
| | + | |
| | + | |
| | <tr> | | <tr> |
| - | <td class="row">LuxI</td>
| + | <td class="row">LuxI</td> |
| - | <td class="row">kinetics of LuxI enzyme</td>
| + | <td class="row">kinetics of LuxI enzyme</td> |
| - | <td class="row">[<sup>AUr</sup>⁄<sub>cell</sub>]</td>
| + | <td class="row">[<sup>AUr</sup>⁄<sub>cell</sub>]</td> |
| - | <td class="row">-</td>
| + | <td class="row">-</td> |
| - | </tr>
| + | </tr> |
| | + | |
| | <tr> | | <tr> |
| - | <td class="row">AiiA</td>
| + | <td class="row">AiiA</td> |
| - | <td class="row">kinetics of AiiA enzyme</td>
| + | <td class="row">kinetics of AiiA enzyme</td> |
| - | <td class="row">[<sup>AUr</sup>⁄<sub>cell</sub>]</td>
| + | <td class="row">[<sup>AUr</sup>⁄<sub>cell</sub>]</td> |
| - | <td class="row">-</td>
| + | <td class="row">-</td> |
| - | </tr>
| + | </tr> |
| | + | |
| | <tr> | | <tr> |
| - | <td class="row">HSL</td>
| + | <td class="row">HSL</td> |
| - | <td class="row">kinetics of HSL</b></td>
| + | <td class="row">kinetics of HSL</b></td> |
| - | <td class="row">[<sup>nM</sup>⁄<sub>(min)</sub>]</td>
| + | <td class="row">[nM]</td> |
| - | <td class="row">-</td>
| + | <td class="row">-</td> |
| - | </tr>
| + | </tr> |
| | + | |
| | <tr> | | <tr> |
| - | <td class="row">N</td>
| + | <td class="row">N</td> |
| - | <td class="row">number of cells</td>
| + | <td class="row">number of cells</td> |
| - | <td class="row">cell</td>
| + | <td class="row">cell</td> |
| - | <td class="row">-</td>
| + | <td class="row">-</td> |
| - | </tr>
| + | </tr> |
| - | </table>
| + | </table> |
| | </center> | | </center> |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <div align="justify"><b><a name="RBS">NOTE</a></b> | + | |
| - | <p>In order to better investigate the range of dynamics of each subpart, every promoter has been studied with 4 different RBSs, so as to develop more knowledge about the state variables in several configurations of RBS' efficiency <a href="#Salis">(<i><b>Salis HM</b> et al. 2009</i>)</a>. Hereafter, referring to the notation "RBSx" we mean, respectively, <a href="http://partsregistry.org/Part:BBa_B0030">RBS30</a>, <a href="http://partsregistry.org/Part:BBa_B0031">RBS31</a>, <a href="http://partsregistry.org/Part:BBa_B0032">RBS32</a>, <a href="http://partsregistry.org/Part:BBa_B0034">RBS34</a>. </p>
| + | |
| - | </div> | + | <div align="justify"><b><a name="RBS">NOTE</a></b><p>In order to better investigate the range of dynamics of each subpart, every promoter has been studied with 4 different RBSs, so as to develop more knowledge about the state variables in several configurations of RBS' efficiency <a href="#Salis">(<i><b>Salis HM</b> et al. 2009</i>)</a>. Hereafter, referring to the notation "RBSx" we mean, respectively, |
| | + | <a href="http://partsregistry.org/Part:BBa_B0030">RBS30</a>, |
| | + | <a href="http://partsregistry.org/Part:BBa_B0031">RBS31</a>, |
| | + | <a href="http://partsregistry.org/Part:BBa_B0032">RBS32</a>, |
| | + | <a href="http://partsregistry.org/Part:BBa_B0034">RBS34</a>. |
| | + | </p></div> |
| | <br> | | <br> |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| - | <a name="CV"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Parameter CV</b> </span></h4> | + | <a name="CV"></a><h4> <span class="mw-headline"> <b>Parameter CV</b> </span></h4> |
| | <center> | | <center> |
| - | <table class="data">
| + | <table class="data"> |
| | <tr> | | <tr> |
| - | <td class="row"><b>Parameter & Species</b></td>
| + | <td class="row"><b>Parameter & Species</b></td> |
| - | <td class="row"><b>BBa_B0030</b></td>
| + | <td class="row"><b>BBa_B0030</b></td> |
| - | <td class="row"><b>BBa_B0031</b></td>
| + | <td class="row"><b>BBa_B0031</b></td> |
| - | <td class="row"><b>BBa_B0032</b></td>
| + | <td class="row"><b>BBa_B0032</b></td> |
| - | <td class="row"><b>BBa_B0034</b></td>
| + | <td class="row"><b>BBa_B0034</b></td> |
| - | </tr>
| + | </tr> |
| | <tr> | | <tr> |
| - | <td class="row">α<sub>p<sub>Tet</sub></sub></td>
| + | <td class="row">α<sub>p<sub>Tet</sub></sub></td> |
| - | <td class="row">3.7</td>
| + | <td class="row">3.7</td> |
| - | <td class="row">ND</td>
| + | <td class="row">ND</td> |
| - | <td class="row">12</td>
| + | <td class="row">12</td> |
| - | <td class="row">5.94</td>
| + | <td class="row">5.94</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">δ<sub>p<sub>Tet</sub></sub></td>
| + | <td class="row">δ<sub>p<sub>Tet</sub></sub></td> |
| - | <td class="row">91.61</td>
| + | <td class="row">91.61</td> |
| - | <td class="row">>>100</td>
| + | <td class="row">>>100</td> |
| - | <td class="row">>100</td>
| + | <td class="row">>100</td> |
| - | <td class="row">40.59</td>
| + | <td class="row">40.59</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">η<sub>p<sub>Tet</sub></sub></td>
| + | <td class="row">η<sub>p<sub>Tet</sub></sub></td> |
| - | <td class="row">23.72</td>
| + | <td class="row">23.72</td> |
| - | <td class="row">>>100</td>
| + | <td class="row">>>100</td> |
| - | <td class="row">57.62</td>
| + | <td class="row">57.62</td> |
| - | <td class="row">47.6</td>
| + | <td class="row">47.6</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">k<sub>p<sub>Tet</sub></sub></td>
| + | <td class="row">k<sub>p<sub>Tet</sub></sub></td> |
| - | <td class="row">4.16</td>
| + | <td class="row">4.16</td> |
| - | <td class="row">>>100</td>
| + | <td class="row">>>100</td> |
| - | <td class="row">14.99</td>
| + | <td class="row">14.99</td> |
| - | <td class="row">5.43</td>
| + | <td class="row">5.43</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">α<sub>p<sub>Lux</sub></sub></td>
| + | <td class="row">α<sub>p<sub>Lux</sub></sub></td> |
| - | <td class="row">10.14</td>
| + | <td class="row">10.14</td> |
| - | <td class="row">7.13</td>
| + | <td class="row">7.13</td> |
| - | <td class="row">2.78</td>
| + | <td class="row">2.78</td> |
| - | <td class="row">5.8</td>
| + | <td class="row">5.8</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">δ<sub>p<sub>Lux</sub></sub></td>
| + | <td class="row">δ<sub>p<sub>Lux</sub></sub></td> |
| - | <td class="row">179.7</td>
| + | <td class="row">179.7</td> |
| - | <td class="row">57.04</td>
| + | <td class="row">57.04</td> |
| - | <td class="row">1317.7</td>
| + | <td class="row">1317.7</td> |
| - | <td class="row">187.2</td>
| + | <td class="row">187.2</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">η<sub>p<sub>Lux</sub></sub></td>
| + | <td class="row">η<sub>p<sub>Lux</sub></sub></td> |
| - | <td class="row">47.73</td>
| + | <td class="row">47.73</td> |
| - | <td class="row">29.13</td>
| + | <td class="row">29.13</td> |
| - | <td class="row">9.75</td>
| + | <td class="row">9.75</td> |
| - | <td class="row">19.3</td>
| + | <td class="row">19.3</td> |
| - | </tr>
| + | </tr> |
| - | <tr>
| + | <tr> |
| - | <td class="row">k<sub>p<sub>Lux</sub></sub></td>
| + | <td class="row">k<sub>p<sub>Lux</sub></sub></td> |
| - | <td class="row">27.5</td>
| + | <td class="row">27.5</td> |
| - | <td class="row">25.81</td>
| + | <td class="row">25.81</td> |
| - | <td class="row">8.46</td>
| + | <td class="row">8.46</td> |
| - | <td class="row">17.86</td>
| + | <td class="row">17.86</td> |
| - | </tr>
| + | </tr> |
| - | </table>
| + | |
| | + | </table> |
| | </center> | | </center> |
| - | <div align="right"><br> | + | <div align="right"><br><small><a href="#indice">^top</a></small></div> |
| - | <small><a href="#indice">^top</a></small></div>
| + | |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <a name="Parameter_estimation"></a> | + | |
| - | <h2> <span class="mw-headline"> <b>Parameter estimation</b></span></h2> | + | |
| | + | |
| | + | |
| | + | <a name="Parameter_estimation"></a><h2> <span class="mw-headline"> <b>Parameter estimation</b></span></h2> |
| | <div style='text-align:justify'>The aim of the model is to predict the behavior of the final closed loop circuit starting from the characterization of single BioBrick parts through a set of well-designed <em>ad hoc</em> experiments. This section presents the experiments performed. | | <div style='text-align:justify'>The aim of the model is to predict the behavior of the final closed loop circuit starting from the characterization of single BioBrick parts through a set of well-designed <em>ad hoc</em> experiments. This section presents the experiments performed. |
| - | As explained before in <a href="#RBS"><span class="toctext"><b>NOTE</b></span></a>, considering a set of 4 RBSs for each subpart expands the range of dynamics and helps us to better understand the interactions between state variables. </div>
| + | As explained before in <a href="#RBS"><span class="toctext"><b>NOTE</b></span></a>, considering a set of 4 RBSs for each subpart expands the range of dynamics and helps us to better understand the interactions between state variables. |
| | + | </div> |
| | + | <br><div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| - | <div align="right"><small><a href="#indice">^top</a></small></div>
| + | |
| - | <br>
| + | |
| - | <a name="Ptet_&_Plux"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Promoter (PTet & pLux)</b> </span></h4> | + | <a name="Ptet_&_Plux"></a><h4> <span class="mw-headline"> <b>Promoter (PTet & pLux)</b> </span></h4> |
| - | <center>
| + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/9/91/Caratterizzazione_ptetN.jpg" class="thumbimage" width="33%">
| + | |
| - | </center>
| + | |
| - | <center>
| + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/7/79/Caratterizzazione_pluxN.jpg" class="thumbimage" width="70%">
| + | |
| - | </center>
| + | |
| | <div style='text-align:justify'> | | <div style='text-align:justify'> |
| - | <p>These are the first parts tested, with the target of learning more about pTet and pLux promoters. In particular, as previously explained in <a href=#RBS>NOTE</a>, for each promoter, we tested four different combinations of promoter-RBS, providing us a set of fundamental building blocks for the subsequent assebly of the closed-loop circuit.</p> | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width:100%;"><img alt="" src="https://static.igem.org/mediawiki/2011/9/91/Caratterizzazione_ptetN.jpg" class="thumbimage" width="33%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | |
| | + | </div> |
| | + | |
| | + | <div style='text-align:justify'> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width:100%;"><img alt="" src="https://static.igem.org/mediawiki/2011/7/79/Caratterizzazione_pluxN.jpg" class="thumbimage" width="70%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | |
| | + | </div> |
| | + | <div style='text-align:justify'><p>These are the first parts tested, with the target of learning more about pTet and pLux promoters. In particular, as previously explained in <a href=#RBS>NOTE</a>, for each promoter, we tested four different combinations of promoter-RBS, providing us a set of fundamental building blocks for the subsequent assebly of the closed-loop circuit.</p> |
| | <p>As shown in the figure below, we considered a range of inductions and we monitored, in time, absorbance (O.D. stands for "optical density") and fluorescence; the two vertical segments for each graph highlight the exponential phase of bacterial growth. S<sub>cell</sub> (namely, synthesis rate per cell) can be derived as a function of inducer concentration, thereby providing the desired input-output relation (inducer concentration versus promoter+RBS activity), which was modelled as a Hill curve:</p> | | <p>As shown in the figure below, we considered a range of inductions and we monitored, in time, absorbance (O.D. stands for "optical density") and fluorescence; the two vertical segments for each graph highlight the exponential phase of bacterial growth. S<sub>cell</sub> (namely, synthesis rate per cell) can be derived as a function of inducer concentration, thereby providing the desired input-output relation (inducer concentration versus promoter+RBS activity), which was modelled as a Hill curve:</p> |
| - | <center> | + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/5/58/Scell.jpg" class="thumbimage" width="45%">
| + | <div align="center"><div class="thumbinner" style="width: 600px;"> |
| - | </center> | + | <a href="https://static.igem.org/mediawiki/2011/5/58/Scell.jpg"> |
| - | <p>However, also Relative Promoter Unit (RPU, <a href="#Kelly"><i><b>Kelly JR</b> et al. 2009</i></a>) has been calculated as a ratio of S<sub>cell</sub> of promoter of interest and the S<sub>cell</sub> of <a href="http://partsregistry.org/Part:BBa_J23101">BBa_J23101</a> (reference to <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>3</sub></em></b></span></a>).</p> | + | <img alt="" src="https://static.igem.org/mediawiki/2011/5/58/Scell.jpg" class="thumbimage" width="45%"></a></div></div> |
| - | <center> | + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/2/26/Box2_new.jpg" class="thumbimage" height="48%" width="120%">
| + | However, also Relative Promoter Unit (RPU, <a href="#Kelly"><i><b>Kelly JR</b> et al. 2009</i></a>) has been calculated as a ratio of S<sub>cell</sub> of promoter of interest and the S<sub>cell</sub> of <a href="http://partsregistry.org/Part:BBa_J23101">BBa_J23101</a> (reference to <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>3</sub></em></b></span></a>).<br> |
| - | </center> | + | |
| | + | <div style='text-align:center; margin-bottom:0px; padding-bottom:0px;'><div class="thumbinner" style="width: 600px;"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/2/26/Box2_new.jpg"> |
| | + | <img alt="" src="https://static.igem.org/mediawiki/2011/2/26/Box2_new.jpg" class="thumbimage" height="48%" width="120%"></a></div></div><br> |
| | + | <div style='text-align:center; font-size: 12px; font-style:italic; margin-top:-20px; padding-top:-20px;'>Data analysis procedure for the determination of promoters activation curve</div> |
| | + | |
| | <p>As shown in the figure, α, as already mentioned, represents the protein maximum synthesis rate, which is reached, in accordance with Hill equation, when the inducer concentration tends to infinite, and, more practically, when the inducer concentration is sufficiently higher than the dissociation constant. Meanwhile the product α*δ stands for the leakage activity (at no induction), liable for protein production (LuxI and AiiA respectively) even in the absence of inducer.</p> | | <p>As shown in the figure, α, as already mentioned, represents the protein maximum synthesis rate, which is reached, in accordance with Hill equation, when the inducer concentration tends to infinite, and, more practically, when the inducer concentration is sufficiently higher than the dissociation constant. Meanwhile the product α*δ stands for the leakage activity (at no induction), liable for protein production (LuxI and AiiA respectively) even in the absence of inducer.</p> |
| | <p>The paramenter η is the Hill's cooperativity constant and it affects the ripidity of transition from the lower and upper boundary of the curve relating S<sub>cell</sub> to the inducer concentration. | | <p>The paramenter η is the Hill's cooperativity constant and it affects the ripidity of transition from the lower and upper boundary of the curve relating S<sub>cell</sub> to the inducer concentration. |
| - | Lastly, k stands for the semi-saturation constant and, in case of η=1, it indicates the concentration of substrate at which half the synthesis rate is achieved. <br>
| + | Lastly, k stands for the semi-saturation constant and, in case of η=1, it indicates the concentration of substrate at which half the synthesis rate is achieved. |
| - | <div align="right"><small><a href="#indice">^top</a></small></div> | + | <br><div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <a name="introduction_to_T9002"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>T9002 introduction</b> </span></h4> | + | |
| - | <div style='text-align:justify'> <em> | + | |
| - | <p>LuxI and AiiA tests have been always performed exploiting the well-characterized BioBrick <a href="http://partsregistry.org/Part:BBa_T9002">BBa_T9002</a>, by which it's possible to quantify exactly the concentration of HSL.</p>
| + | <a name="introduction_to_T9002"></a><h4> <span class="mw-headline"> <b>T9002 introduction</b> </span></h4> |
| - | <center>
| + | <div style='text-align:justify'> |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/c/c2/T9002.jpg" class="thumbimage" width="110%">
| + | <em> |
| - | </center>
| + | <p>LuxI and AiiA tests have been always performed exploiting the well-characterized BioBrick <a href="http://partsregistry.org/Part:BBa_T9002">BBa_T9002</a>, by which it's possible to quantify exactly the concentration of HSL.</p> |
| - | <p>This is a biosensor which receives HSL concentration as input and returns GFP intensity (more precisely S<sub>cell</sub>) as output.<a href="#Canton"> (<i><b>Canton</b> et al. 2008</i>).</a> According to this, it is necessary to understand the input-output relationship: so, a T9002 "calibration" curve is plotted for each test performed.</p>
| + | <div align="center"><div class="thumbinner" style="width: 500px;"><img alt="" src="https://static.igem.org/mediawiki/2011/c/c2/T9002.jpg" class="thumbimage" width="110%"></a></div></div> |
| - | <br>
| + | <p>This is a biosensor which receives HSL concentration as input and returns GFP intensity (more precisely S<sub>cell</sub>) as output.<a href="#Canton"> (<i><b>Canton</b> et al. 2008</i>).</a> |
| - | <br>
| + | According to this, it is necessary to understand the input-output relationship: so, a T9002 "calibration" curve is plotted for each test performed.</p><br><br> |
| - | </em> </div>
| + | </em> |
| | + | </div> |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| - | <a name="Enzymes"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>AiiA & LuxI</b> </span></h4> | + | |
| | + | |
| | + | <a name="Enzymes"></a><h4> <span class="mw-headline"> <b>AiiA & LuxI</b> </span></h4> |
| | + | <div style='text-align:justify'><p>This paragraph explains how parameters of equation (3) are estimated. The target is to learn the AiiA degradation and LuxI production mechanisms in addiction to HSL intrinsic degradation, in order to estimate V<sub>max</sub>, K<sub>M,LuxI</sub>, k<sub>cat</sub>, K<sub>M,AiiA</sub> and γ<sub>HSL</sub> parameters. We adopt tests composed of two steps. In the first one, the following BioBrick parts are used:</p> |
| | + | </div> |
| | + | |
| | <div style='text-align:justify'> | | <div style='text-align:justify'> |
| - | <p>This paragraph explains how parameters of equation (3) are estimated. The target is to learn the AiiA degradation and LuxI production mechanisms in addiction to HSL intrinsic degradation, in order to estimate V<sub>max</sub>, K<sub>M,LuxI</sub>, k<sub>cat</sub>, K<sub>M,AiiA</sub> and γ<sub>HSL</sub> parameters. We adopt tests composed of two steps. In the first one, the following BioBrick parts are used:</p>
| + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width:100%;"><img alt="" src="https://static.igem.org/mediawiki/2011/8/88/Caratterizzazione_aiia.JPG" class="thumbimage" width="32%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | </div> | | </div> |
| - | <center>
| + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/8/88/Caratterizzazione_aiia.JPG" class="thumbimage" width="32%">
| + | |
| - | </center>
| + | |
| | <div style='text-align:justify'> | | <div style='text-align:justify'> |
| - | <center>
| + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/4/48/Caratterizzazione_luxIN.jpg" class="thumbimage" width="28%">
| + | <table align='center' width='100%'> |
| - | </center> | + | <tr> |
| - | <div style='text-align:justify'> | + | <td> |
| - | <p>Based on our <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>3</sub></em></b></span></a> and <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, we are able to determine AiiA and LuxI concentrations, provided we have yet characterized pTet-RBSx contructs<a name='t9002'></a>. In particular, referring to <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, in exponential growth the equilibrium of the enzymes is conserved. Due to a known induction of aTc, the steady-state level per cell can be calculated:</p>
| + | <div style='text-align:center'><div class="thumbinner" style="width:100%;"><img alt="" src="https://static.igem.org/mediawiki/2011/4/48/Caratterizzazione_luxIN.jpg" class="thumbimage" width="28%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | </div> | | </div> |
| - | <center> | + | |
| - | <img alt="" src="https://static.igem.org/mediawiki/2011/7/74/Aiia_cost.jpg" class="thumbimage" width="120%">
| + | <div style='text-align:justify'><p>Based on our <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>3</sub></em></b></span></a> and <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, we are able to determine AiiA and LuxI concentrations, provided we have yet characterized pTet-RBSx contructs<a name='t9002'></a>. In particular, referring to <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, in exponential growth the equilibrium of the enzymes is conserved. Due to a known induction of aTc, the steady-state level per cell can be calculated:</p></div> |
| - | </center> | + | |
| - | <p>Then, as a second step, we monitor in separate experiments HSL synthesis and degradation caused by the activities of the enzymes. In other words, our idea is to control the degradation of HSL versus time. ATc activates pTet and, later, a certain concentration of HSL is introduced. Then, at fixed times, O.D.<sub>600</sub> and HSL concentration are monitored using Tecan and T9002 biosensor.</p> | + | <div style='text-align:justify'><div class="thumbinner" style="width: 500px;"> |
| - | <p>For example for AiiA dependent HSL degradation, we have:</p> | + | <a href="https://static.igem.org/mediawiki/2011/7/74/Aiia_cost.jpg"> |
| - | <center> | + | <img alt="" src="https://static.igem.org/mediawiki/2011/7/74/Aiia_cost.jpg" class="thumbimage" width="120%"></a></div></div> |
| - | <img src="https://static.igem.org/mediawiki/2011/9/99/Degradation.jpg" class="thumbimage" width="140%">
| + | |
| - | </center> | + | <p>Then, as a second step, we monitor in separate experiments HSL synthesis and degradation caused by the activities of the enzymes. In other words, our idea is to control the degradation of HSL versus time. ATc activates pTet and, later, a certain concentration of HSL is introduced. Then, at fixed times, O.D.<sub>600</sub> and HSL concentration are monitored using Tecan and T9002 biosensor.</p><p>For example for LuxI dependent HSL production, we have:</p> |
| | + | |
| | + | <table align='center' width='100%' style='margin-bottom:0px; padding-bottom:0px;'> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 70%;"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/9/99/Degradation.jpg"> |
| | + | <img src="https://static.igem.org/mediawiki/2011/9/99/Degradation.jpg" class="thumbimage" width="140%"></a></div></div> |
| | </table> | | </table> |
| | + | <div style='text-align:center; font-size: 12px; font-style:italic; margin-top:0px; padding-top:0px;'>Graphical representation of LuxI dependent HSL production, determined through T9002 HSL biosensor</div> |
| | + | |
| | + | <br><p>Therefore, considering for a determined promoter-RBSx couple, several induction of aTc and, for each of them, several samples of HSL concentration during time, parameters V<sub>max</sub>, k<sub>M,LuxI</sub>, k<sub>cat</sub> and k<sub>M,AiiA</sub> can be estimated, through numerous iterations of an algorithm implemented in MATLAB.</p> |
| | + | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| - | <p>Therefore, considering for a determined promoter-RBSx couple, several induction of aTc and, for each of them, several samples of HSL concentration during time, parameters V<sub>max</sub>, k<sub>M,LuxI</sub>, k<sub>cat</sub> and k<sub>M,AiiA</sub> can be estimated, through numerous iterations of an algorithm implemented in MATLAB.</p> | + | <br> |
| | + | |
| | + | <a name="N"></a><h4> <span class="mw-headline"> <b>N</b> </span></h4> |
| | + | <div style='text-align:justify'>The parameters N<sub>max</sub> and μ can be calculated from the analysis of the OD<sub>600</sub> produced by our MGZ1 culture. In particular, μ is derived as the slope of the log(O.D.<sub>600</sub>) growth curve. Counting the number of cells of a saturated culture would be considerably complicated, so N<sub>max</sub> is determined with a proper procedure. The aim here is to derive the linear proportional coefficient Θ between O.D'.<sub>600</sub> and N: this constant can be estimated as the ratio between absorbance (read from TECAN) and the respective number of CFU on a petri plate. Finally, N<sub>max</sub> is calcultated as Θ*O.D'.<sub>600</sub> |
| | + | <a href="#Pasotti">(<i><b>Pasotti L</b> et al. 2010</i>)</a>. |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | + | </div> |
| | + | |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <a name="N"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>N</b> </span></h4> | + | |
| - | <div style='text-align:justify'>The parameters N<sub>max</sub> and μ can be calculated from the analysis of the OD<sub>600</sub> produced by our MGZ1 culture. In particular, μ is derived as the slope of the log(O.D.<sub>600</sub>) growth curve. Counting the number of cells of a saturated culture would be considerably complicated, so N<sub>max</sub> is determined with a proper procedure. The aim here is to derive the linear proportional coefficient Θ between O.D'.<sub>600</sub> and N: this constant can be estimated as the ratio between absorbance (read from TECAN) and the respective number of CFU on a petri plate. Finally, N<sub>max</sub> is calcultated as Θ*O.D'.<sub>600</sub> <a href="#Pasotti">(<i><b>Pasotti L</b> et al. 2010</i>)</a>. | + | <a name="Degradation_rates"></a><h4> <span class="mw-headline"> <b>Degradation rates</b> </span></h4> |
| - | <div align="right"><small><a href="#indice">^top</a></small></div>
| + | <div style='text-align:justify'>The parameters γ<sub>LuxI</sub> and γ<sub>AiiA</sub> are taken from literature since they contain LVA tag for rapid degradation. Instead, approximating HSL kinetics as a decaying exponential, γ<sub>HSL</sub> can be derived as the slope of the log(concentration), which can be monitored through <a href="http://partsregistry.org/Part:BBa_T9002">BBa_T9002</a>. In case of pH=6, γ<sub>HSL</sub>=0. |
| | </div> | | </div> |
| | + | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | <br> | | <br> |
| | <br> | | <br> |
| - | <a name="Degradation_rates"></a> | + | |
| - | <h4> <span class="mw-headline"> <b>Degradation rates</b> </span></h4> | + | |
| - | <div style='text-align:justify'>The parameters γ<sub>LuxI</sub> and γ<sub>AiiA</sub> are taken from literature since they contain LVA tag for rapid degradation. Instead, approximating HSL kinetics as a decaying exponential, γ<sub>HSL</sub> can be derived as the slope of the log(concentration), which can be monitored through <a href="http://partsregistry.org/Part:BBa_T9002">BBa_T9002</a>. </div> | + | <a name="Simulations"></a><h1><span class="mw-headline"> <b>Simulations</b> </span></h1> |
| | + | <div> |
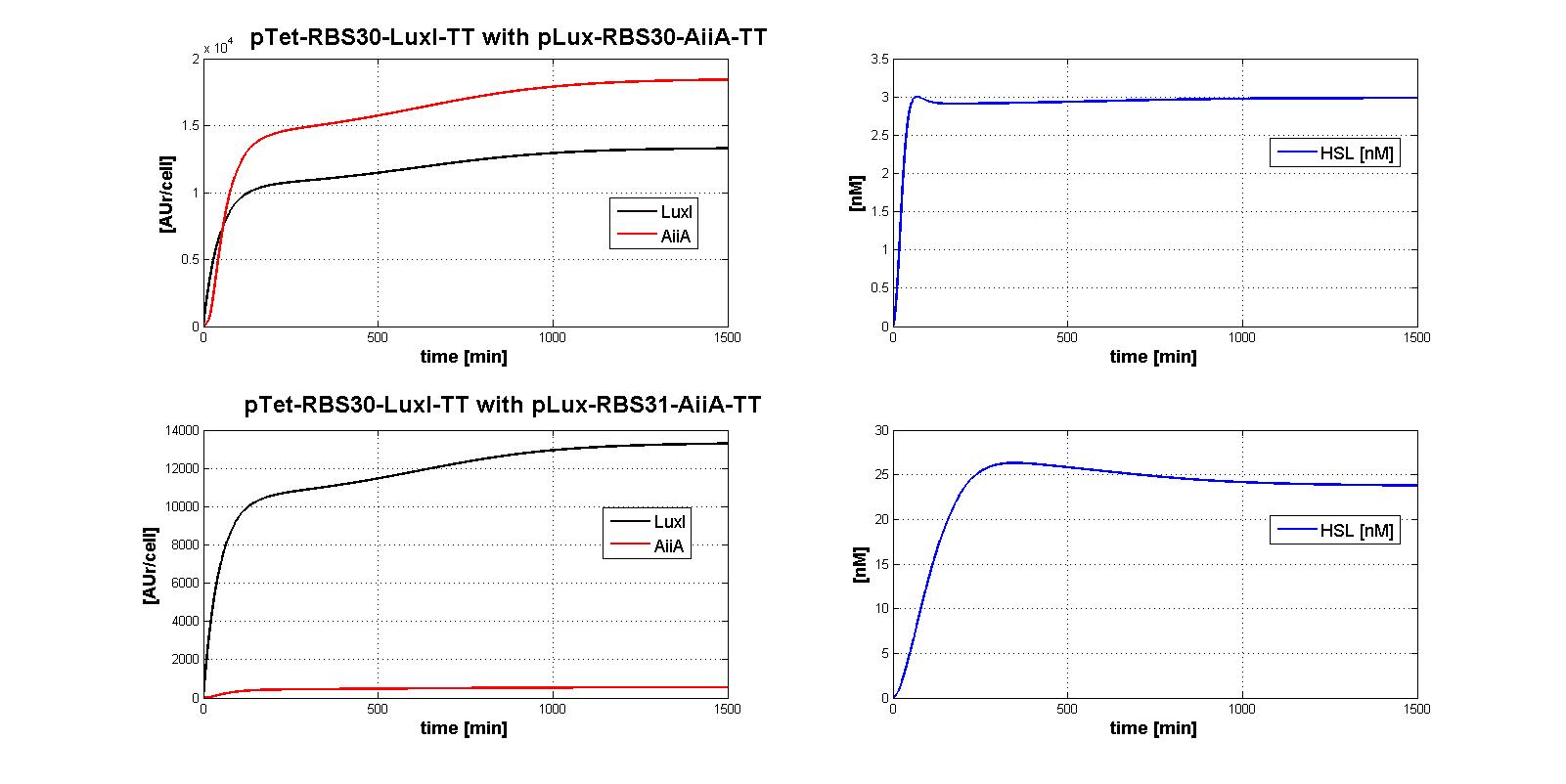
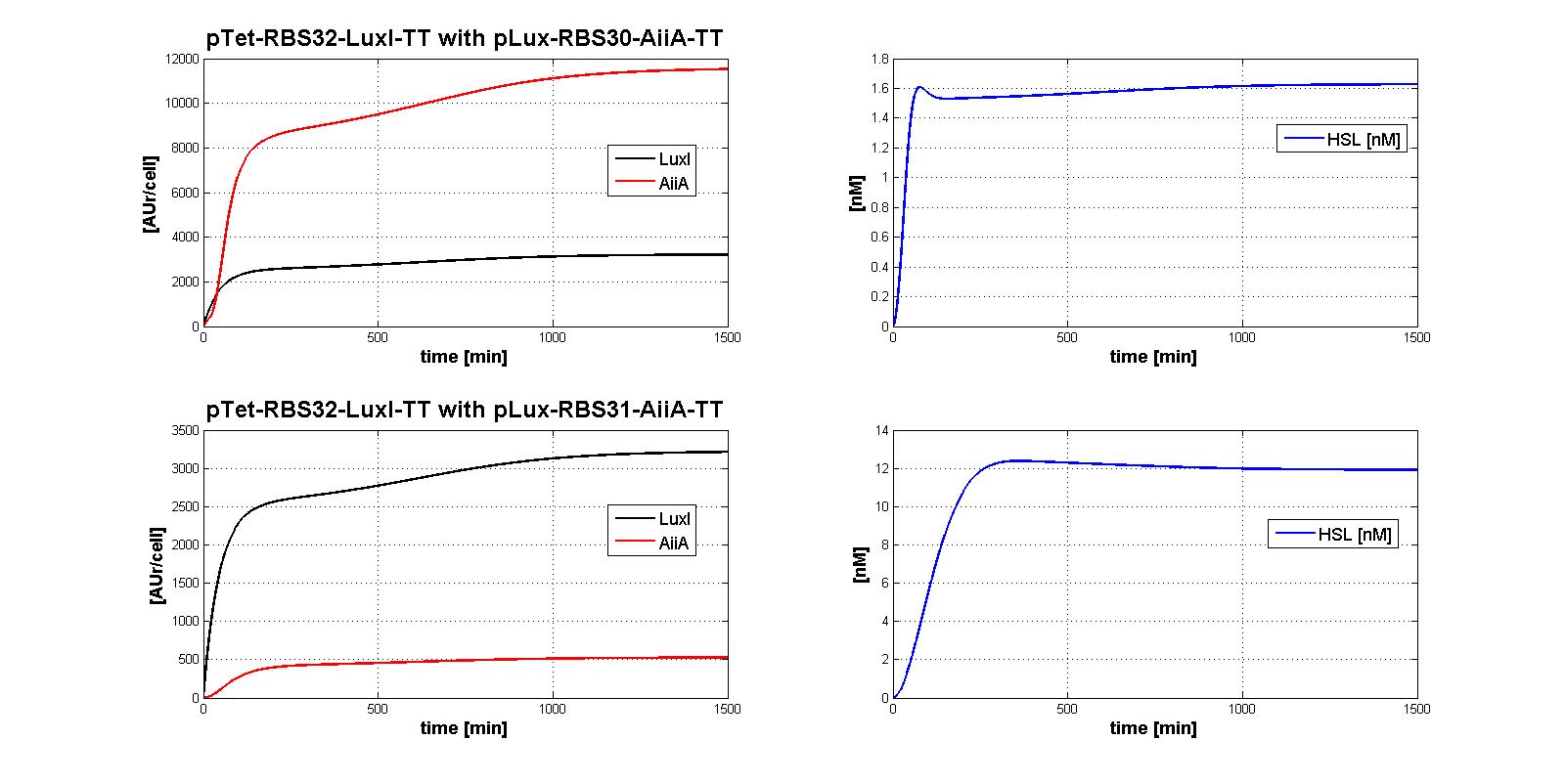
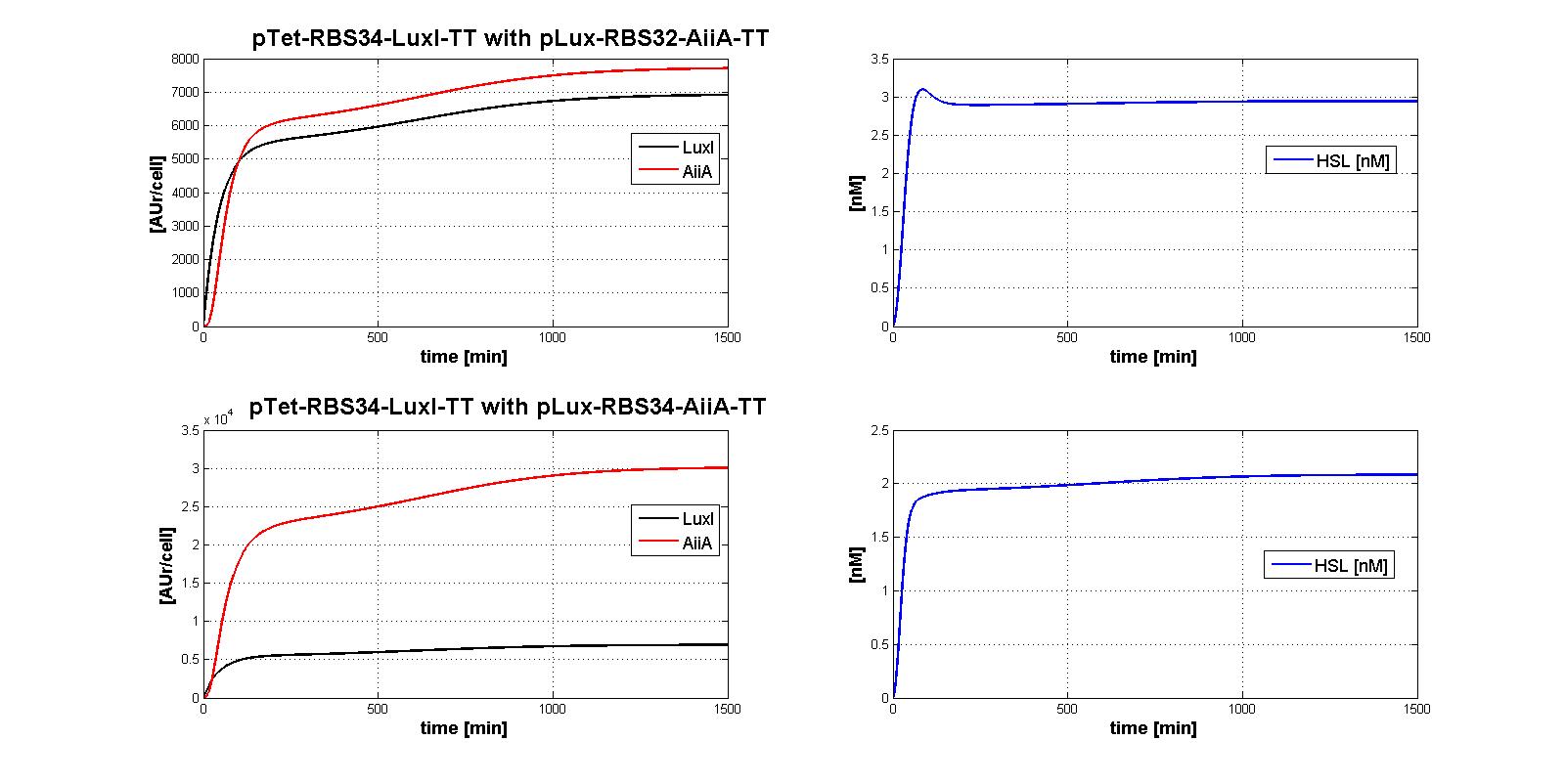
| | + | The whole control circuit has been simulated and here the simulation results are presented. <br> |
| | + | All the combinations of pTet-RBSx and pLux-RBSx were simulated using ODEs', in case of aTc=100 ng/ml. |
| | + | As explained in <a href="https://2011.igem.org/Team:UNIPV-Pavia/Parts/Characterized#AiiA">AiiA gene - BBa_C0060 section</a>, parameters k<sub>cat</sub> and k<sub>M,AiiA</sub> were difficult to estimate from the collected data. |
| | + | <br> Here simulations are performed assuming reasonable values for k<sub>cat</sub> and k<sub>M,AiiA</sub> (1*10<sup>-9</sup> [1/(min*cell)] and k<sub>M,AiiA</sub>=5000 [AUr/cell], respectively).<br> |
| | + | |
| | + | Obviously, increasing the k<sub>cat</sub> value, the HSL steady-state concentration decreases. |
| | + | Nevertheless, if you consider 100-fold variation of k<sub>cat</sub> value, the steady state of HSL is in the range about [0.08-0.7] nM. |
| | + | </div> |
| | + | |
| | + | |
| | + | <br> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/0/0d/Ptet_RBS30plux_RBS31simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/0/0d/Ptet_RBS30plux_RBS31simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/f/f7/Ptet_RBS30plux_RBS34simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/f/f7/Ptet_RBS30plux_RBS34simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/4/4a/Ptet_RBS32plux_RBS31simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/4/4a/Ptet_RBS32plux_RBS31simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/d/d8/Ptet_RBS32plux_RBS34simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/d/d8/Ptet_RBS32plux_RBS34simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/0/0c/Ptet_RBS34plux_RBS31simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/0/0c/Ptet_RBS34plux_RBS31simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | |
| | + | <div style='text-align:justify'><div class="thumbinner" style="width: 850px;"><a href="https://static.igem.org/mediawiki/2011/f/fc/Ptet_RBS34plux_RBS34simul.jpg"><img alt="" src="https://static.igem.org/mediawiki/2011/f/fc/Ptet_RBS34plux_RBS34simul.jpg" class="thumbimage" width="85%" height="55%"></a></div></div> |
| | + | <br> |
| | + | <br> |
| | + | |
| | + | |
| | + | |
| | + | |
| | + | |
| | + | <a name="Sensitivity_Analysis"></a><h1> <span class="mw-headline"> <b>Sensitivity Analysis of the steady state of enzyme expression in exponential phase</b> </span></h1> |
| | + | |
| | + | <p>In this paragraph we investigate the theoretical behaviour of our circuit in the cell culture exponential growth phase. According to this, we first derive, under feasible hypotheses, the steady state condition for the enzymes and HSL concentration in that phase. Then we perform a sensitivity analysis relating the output of our system (HSL) to input (aTc) and system parameters.</p> |
| | + | |
| | <div align="right"><small><a href="#indice">^top</a></small></div> | | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | + | |
| | + | <a name="Steady state of enzyme expression"></a><h2> <span class="mw-headline"> <b>Steady state of enzyme expression</b> </span></h2> |
| | + | |
| | + | |
| | + | <p> Based on <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, we can formulate the steady state expressions during the exponential growth phase. Adding other considerations about the involved processes, it is possible to further simplify the steady state equations. In particular, one concern relates to the number of cells N (in the order of 10^7), which is far lower than N<sub>max</sub> (10^9). The other pertains to γ*HSL parameter, which can be neglected compared to the other two terms of the third equation, considering pH=6. Based on this assumptions, equation (4) of the system becomes dN/dt=μN. Moreover, from equation (3), after having removed the third term, we can simplify the N parameter, since it is common to the remaining two terms. On a biological point of view, this implies that AiiA, LuxI and HSL undergo only minor changes through time, thereby allowing to derive their steady state expressions:</p> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/3/32/LuxI_SS.jpg"> |
| | + | <img src="https://static.igem.org/mediawiki/2011/3/32/LuxI_SS.jpg" class="thumbimage" width="83%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | <p> The first equation is independent from the second and third ones, enabling us to directly determine LuxI steady state expression during the exponential growth phase. On the contrary, second and third equations depend each other in defining the value of AiiA and HSL respectively, because the former is a function of HSL, while the latter is a function of AiiA. So we could resolve a system of two equations, first by expliciting one of the two variables with respect to the other, and then substituting its expression in order to determine the other variable possible values. This would bring a complex mathematical formulation, which is not helpful in understanding the influence of the various model parameters on the output HSL. |
| | + | On the other hand, AiiA and HSL values can also be graphically determined from the intersection of the curves derived from these two equations, if we explicit HSL as a function of AiiA (or, alternatively, AiiA as a function of HSL). It is easy to discover that these two curves represent rectangular hyperbolae (the first one only under a simple approximation, explained below) whose tails intersect each other at a particular point, corresponding to the searched values for AiiA and HSL.</p> |
| | + | <div>For a rectangular hyperbola (RH), we have:</div> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"><a href="" class="image"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/7/75/UNIPV_Rectangular_hyperbola_general.jpg"> |
| | + | <img src="https://static.igem.org/mediawiki/2011/7/75/UNIPV_Rectangular_hyperbola_general.jpg" class="thumbimage" width="14%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | <p>centered at O(-d/c;a/c), with the vertical asymptote x=-d/c and the horizontal asymptote y=a/c</p> |
| | + | <p>From equation (2), we have:</p> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"><a href="" class="image"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/3/3a/UNIPV_eta_root_HSL.jpg"> |
| | + | <img src="https://static.igem.org/mediawiki/2011/3/3a/UNIPV_eta_root_HSL.jpg" class="thumbimage" width="62%"></a> |
| | + | </div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | <p> We can introduce the simplification to remove the η<sub>pLux</sub> exponent to the entire expression in the right hand side of the equation, thereby obtaining a rectangular hyperbola; even if this leads to a slight change in the curve behaviour, it allows to more clearly understand the relation between HSL and AiiA. As pertains to equation 3, its steady state relationship during the exponential growth is more immediately identifiable as a rectangular hyperbola. Below the two RHs equations are provided, togheter with the table of parameters.</p> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/1/11/RH1_UNIPV_HSL.jpg"><img src="https://static.igem.org/mediawiki/2011/1/11/RH1_UNIPV_HSL.jpg" class="thumbimage" width="50%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <tr> |
| | + | <td> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"> |
| | + | <a href="https://static.igem.org/mediawiki/2011/4/4b/RH2_UNIPV_HSL.jpg" class="image"> |
| | + | <img src="https://static.igem.org/mediawiki/2011/4/4b/RH2_UNIPV_HSL.jpg" class="thumbimage" width="70%"></a></div></div> |
| | + | </td> |
| | + | </tr> |
| | + | </table> |
| | <br> | | <br> |
| | + | |
| | + | |
| | + | <center> |
| | + | <table class="data"> |
| | + | <tr> |
| | + | <td class="row"><b>Parameter</b></td> |
| | + | <td class="row"><b>RH1</b></td> |
| | + | <td class="row"><b>RH2</b></td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">a</sub></sub></td> |
| | + | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub></td> |
| | + | <td class="row">(γ<sub>AiiA</sub>+μ)*(k<sub>pLux</sub>)<sup>ηpLux</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">b</td> |
| | + | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub>*k<sub>M,AiiA</sub></td> |
| | + | <td class="row">-α<sub>pLux</sub>*δ<sub>pLux</sub>*(k<sub>pLux</sub>)<sup>ηpLux</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">c</sub></sub></td> |
| | + | <td class="row">k<sub>cat</sub></span></td> |
| | + | <td class="row">-γ<sub>AiiA</sub>-μ</td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">d</td> |
| | + | <td class="row">0</td> |
| | + | <td class="row">α<sub>pLux</sub></td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">Horizontal asymptote</td> |
| | + | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub>/k<sub>cat</sub></td> |
| | + | <td class="row">a/c=(k<sub>pLux</sub>)<sup>ηpLux</sup></td> |
| | + | </tr> |
| | + | |
| | + | <tr> |
| | + | <td class="row">Vertical asymptote</td> |
| | + | <td class="row">0</td> |
| | + | <td class="row">-d/c=α<sub>pLux</sub>/(γ<sub>AiiA</sub>+μ)</td> |
| | + | </tr> |
| | + | </table> |
| | + | |
| | + | </center> |
| | + | |
| | + | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | + | |
| | + | <a name="Sensitivity analysis"></a><h2><br> |
| | + | <span class="mw-headline"> <b>Sensitivity analysis</b> </span></h2> |
| | + | |
| | + | <p> Now, it is interesting to conduct some qualitative and quantitative considerations about our system sensitivity to its parameters and aTc input signal.</p> |
| | + | <div> First of all, we analyze how the HSL output can be regulated by changing the characteristics of our RHs.</div><div>Referring to the first rectangular hyperbola, we recognize that its vertical asymptote could be varied by changing α<sub>p<sub>Lux</sub></sub></sub></sub> value (assuming fixed γ<sub>AiiA</sub> and μ). In particular, thanks to the four Plux-RBSx constructs realized, we can vary α<sub>p<sub>Lux</sub></sub></sub></sub> more than a hundred factor. This can significantly shift the vertical asymptote, bringing this first RH farther or nearer the second one (whose vertical asymptote is the ordinate axis), thereby providing an intersection at higher AiiA and lower HSL values, or vice versa. The following two figures highlight this aspect.</div><br> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <div><div class="thumbinner"><a href="https://static.igem.org/mediawiki/2011/4/45/Iperbole_eq_3_as_ver2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/4/45/Iperbole_eq_3_as_ver2.jpg" class="thumbimage" width="100%"></a></div></div> |
| | + | </table> |
| | + | |
| | + | <table width="100%" align="center"> |
| | + | <div style="WIDTH: 100%" class="thumbinner"> |
| | + | <a class="image" href="https://static.igem.org/mediawiki/2011/9/97/UNIPV_inters_RH_ver_alfa_plux_acceptable_values2.jpg"><img class="thumbimage" src="https://static.igem.org/mediawiki/2011/9/97/UNIPV_inters_RH_ver_alfa_plux_acceptable_values2.jpg" width="100%"></a> |
| | + | </div> |
| | + | <tbody></tbody> |
| | + | </table> |
| | + | |
| | + | |
| | + | <p>From the above figures, it is also clear that HSL steady state value is not very sensitive to α<sub>p<sub>Lux</sub></sub></sub></sub>, at least when this parameter presents values greater than unity, because this brings the two curves to intersect in their low slope regions.</p> |
| | + | <p>Referring to RH2, the only adjustable asymptote is the horizontal one, that we can move upward or downward by altering VLuxI, which indirectly depends on aTc.</p> |
| | + | |
| | + | <table align='center' width='100%'> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"><a href="https://static.igem.org/mediawiki/2011/0/04/UNIPV_RH2_eq2_as_or_corrected2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/0/04/UNIPV_RH2_eq2_as_or_corrected2.jpg" class="thumbimage" width="95%"></a></div></div> |
| | + | </table> |
| | + | |
| | + | <p>A further deepening in the exponential phase analysis involves determining the characteristics of the input-output relation. Our closed loop system can be realized with two alternative purposes in mind:</p> |
| | + | <ol> |
| | + | <li> realizing a circuit able to adapt HSL output depending on aTc input concentration. This requires a good sensitivity between input and output.</li> |
| | + | <li> designing a robust HSL concentration controller, which is immune to the input noise and offers a constant and defined amount of HSL. In this case HSL level should be appropriately tuned during the design stage, by choosing the correct strength of promoter-RBSx complexes.</li> |
| | + | </ol> |
| | + | |
| | + | <p>Now,again considering the system of equations, it is easy to observe that HSL dependence on aTc input passes through two Hill equations. The former describes aTc driven LuxI synthesis, while the latter models LuxI dependent HSL synthesis rate. Therefore, in order to achieve a high aTc sensitivity, it is advisable to tune aTc and LuxI levels so that they place outside the saturation regions of their Hill curves. In this regard, it is possible to determine a closed form expression relating HSL to aTc, if we hypothesize that both aTc and LuxI are far lower than their respective half-saturation constant (k_ptet and Km), thus simplifying the Hills with a first order relation:</p> |
| | + | |
| | <br> | | <br> |
| - | <a name="Simulations"></a> | + | |
| - | <h1><span class="mw-headline"> <b>Simulations</b> </span></h1> | + | <table align='center' width='100%'> |
| | + | <div style='text-align:center'><div class="thumbinner" style="width: 100%;"><a href="https://static.igem.org/mediawiki/2011/d/dd/UNIPV_Imply_sensitivity.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/d/dd/UNIPV_Imply_sensitivity.jpg" class="thumbimage" width="80%"></a></div></div> |
| | + | </table> |
| | + | |
| | + | <div align="right"><small><a href="#indice">^top</a></small></div> |
| | + | |
| | + | <a name="References"></a><h1><span class="mw-headline"> <b>References</b> </span></h1> |
| | <div style='text-align:justify'> | | <div style='text-align:justify'> |
| - | <p>On a biological level, the ability to control the concentration of a given molecule reveals itself as fundamental in limiting the metabolic burden of the cell; moreover, in the particular case of HSL signalling molecules, this would give the possibility to regulate quorum sensing-based population behaviours. In this section we present some simulations of another circuit, which could validate the concept of the closed-loop model we have discussed so far.</p>
| + | |
| - | <p>In order to see that, we implemented and simulated in Matlab an open loop circuit, similar to <b>CTRL+<em>E</em></b>, except for the constitutive production of AiiA.</p>
| + | <ol type='1'> |
| - | <center>
| + | |
| - | <img src="https://static.igem.org/mediawiki/2011/b/b6/Sim_closed.jpg" class="thumbimage" width="100%">
| + | <a name="Braun"></a> |
| - | </center>
| + | <li>Braun D, Basu S, Weiss R (2005) <b>Parameter estimation for two synthetic gene networks: a case study </b> |
| - | <center>
| + | <i>ICASSP '05 </i> 5:v/769-v/772. </li> <br> |
| - | <img src="https://static.igem.org/mediawiki/2011/4/4b/Sim_open.jpg" class="thumbimage" width="100%">
| + | |
| - | </center>
| + | <a name="Canton"></a> |
| - | <div align="right"><small><a href="#indice">^top</a></small></div>
| + | <li>Canton B, Labno A, Endy D. (2008) <b>Refinement and standardization of synthetic biological parts and devices. </b> <i> Nat Biotechnol. </i> 26(7):787-93. </li> <br> |
| - | <br>
| + | |
| - | <br>
| + | <a name="Danino"></a> |
| - | <a name="Sensitivity_Analysis"></a>
| + | <li>Danino T, Mondragón-Palomino O, Tsimring L et al. (2010) <b>A synchronized quorum of genetic clocks. </b> <i>Nature. </i> 463(7279):326-30. </li> <br> |
| - | <h1> <span class="mw-headline"> <b>Sensitivity Analysis of the steady state of enzyme expression in exponential phase</b> </span></h1>
| + | |
| - | <p>In this paragraph we investigate the theoretical behaviour of our circuit in the cell culture exponential growth phase. According to this, we first derive, under feasible hypotheses, the steady state condition for the enzymes and HSL concentration in that phase. Then we perform a sensitivity analysis relating the output of our system (HSL) to input (aTc) and system parameters.</p>
| + | <a name="Endler"></a> |
| - | <a name="Steady state of enzyme expression"></a>
| + | <li>Endler L, Rodriguez N, Juty N et al. (2009) <b>Designing and encoding models for synthetic biology. </b> <i>J. R. Soc. Interface </i> 6:S405-S417. </li> <br> |
| - | <h2> <span class="mw-headline"> <b>Steady state of enzyme expression</b></span></h2>
| + | |
| - | <p> Based on our <a href="#Hypothesis"><span class="toctext"><b><em>HP<sub>4</sub></em></b></span></a>, we can formulate the steady state expressions during the exponential growth phase. Adding other considerations about the involved processes, it is possible to add further simplifications to the steady state equations. In particular, one concern relates to the number of cells N (in the order of 3*10^3), which is far lower than N<sub>max</sub> (10^9). The other pertains to γ*HSL parameter, whch can be neglected compared to the other two terms of the third equation. Based on this assumptions, equation (4) of the system becomes dN/dt=μN. Moreover, from equation (3), after having removed the third term, we can simplify the N parameter, since it is common to the remaining two terms. On a biological point of view, this implies that AiiA, LuxI and HSL undergo only minor changes through time, thereby allowing to derive their steady state expressions:</p>
| + | <a name="Kelly"></a> |
| - | <center>
| + | <li>Kelly JR, Rubin AJ, Davis JH et al. (2009) <b>Measuring the activity of BioBrick promoters using an in vivo reference standard.</b> <i> J. Biol. Eng.</i> 3:4.</li> <br> |
| - | <img alt="File:LuxI SS.jpg" src="https://static.igem.org/mediawiki/2011/3/32/LuxI_SS.jpg" class="thumbimage" width="83%"></a>
| + | |
| - | </center>
| + | <a name="Pasotti"></a> |
| - | <p> The first equation is independent from the second and third ones, enabling us to directly determine LuxI steady state expression during the exponential growth phase. On the contrary, second and third equations depend each other in defining the value of AiiA and HSL respectively, because the former is a function of HSL, while the latter is a function of AiiA. So we could resolve a system of two equations, first by expliciting one of the two variables with respect to the other, and then substituting its expression in order to determine the other variable possible values. This would bring a complex mathematical formulation, which is not helpful in understanding the influence of the various model parameters on the output HSL.
| + | <li>Pasotti L, Quattrocelli M, Galli D et al. (2011) <b>Multiplexing and demultiplexing logic functions for computing signal processing tasks in synthetic biology. </b> |
| - | On the other hand, AiiA and HSL values can also be graphically determined from the intersection of the curves derived from these two equations, if we explicit HSL as a function of AiiA (or, alternatively, AiiA as a function of HSL). It is easy to discover that these two curves represent rectangular hyperbolae (the first one only under a simple approximation, explained below) whose tails intersect each other at a particular point, corresponding to the searched values for AiiA and HSL.</p>
| + | <i>Biotechnol. J. </i>6(7):784-95. </li> <br> |
| - | <p>For a rectangular hyperbola (RH), we have:</p>
| + | |
| - | <center>
| + | <a name="Salis"></a> |
| - | <img alt="File:UNIPV Rectangular hyperbola general.jpg" src="https://static.igem.org/mediawiki/2011/7/75/UNIPV_Rectangular_hyperbola_general.jpg" class="thumbimage" width="14%">
| + | <li>Salis H M, Mirsky E A, Voight C A (2009)<b> Automated design of synthetic ribosome binding sites to control protein expression. </b> <i>Nat. Biotechnol.</i>27:946-950. |
| - | </center>
| + | </li><br> |
| - | <p>centered at O(-d/c;a/c), with the vertical asymptote x=-d/c and the horizontal asymptote y=a/c</p>
| + | |
| - | <p>From equation 2, we have:</p>
| + | |
| - | <center>
| + | </ol> |
| - | <img alt="File:UNIPV eta root HSL.jpg" src="https://static.igem.org/mediawiki/2011/3/3a/UNIPV_eta_root_HSL.jpg" class="thumbimage" width="62%">
| + | |
| - | </center>
| + | |
| - | <p> We can introduce the simplification to remove the ηplux exponent to the entire expression in the right hand side of the equation, thereby obtaining a rectangular hyperbola; even if this leads to a slight change in the curve behaviour, it allows to more clearly understand the relation between HSL and AiiA. As pertains to equation 3, its steady state approximation during the exponential growth is more immediately identifiable as a rectangular hyperbola. Below the two RHs equations are provided, togheter with the table of parameters.</p>
| + | |
| - | <center>
| + | |
| - | <img alt="File:RH1 UNIPV HSL.jpg" src="https://static.igem.org/mediawiki/2011/1/11/RH1_UNIPV_HSL.jpg" class="thumbimage" width="50%">
| + | |
| - | </center>
| + | |
| - | <center>
| + | |
| - | <img alt="File:RH2 UNIPV HSL.jpg" src="https://static.igem.org/mediawiki/2011/4/4b/RH2_UNIPV_HSL.jpg" class="thumbimage" width="70%">
| + | |
| - | </center>
| + | |
| - | <br>
| + | |
| - | <center>
| + | |
| - | <table class="data">
| + | |
| - | <tr>
| + | |
| - | <td class="row"><b>Parameter</b></td>
| + | |
| - | <td class="row"><b>RH1</b></td>
| + | |
| - | <td class="row"><b>RH2</b></td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">a</sub></sub></td>
| + | |
| - | <td class="row">(γ<sub>AiiA</sub>+μ)*(k<sub>pLux</sub>)<sup>ηpLux</td>
| + | |
| - | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub></td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">b</td>
| + | |
| - | <td class="row">-α<sub>pLux</sub>*δ<sub>pLux</sub>*(k<sub>pLux</sub>)<sup>ηpLux</td>
| + | |
| - | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub>*k<sub>M,LuxI</sub></td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">c</sub></sub></td>
| + | |
| - | <td class="row">-γ<sub>AiiA</sub>+μ</td>
| + | |
| - | <td class="row">k<sub>cat</sub>*<span style="text-decoration:overline;" >AiiA</span></td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">d</td>
| + | |
| - | <td class="row">α<sub>pLux</sub></td>
| + | |
| - | <td class="row">0</td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">Horizontal asymptote</td>
| + | |
| - | <td class="row">a/c=(k<sub>pLux</sub>)<sup>ηpLux</sup></td>
| + | |
| - | <td class="row"><span style="text-decoration:overline;" > V</span><sub>LuxI</sub>/k<sub>cat</sub></td>
| + | |
| - | </tr>
| + | |
| - | <tr>
| + | |
| - | <td class="row">Vertical asymptote</td>
| + | |
| - | <td class="row">-d/c=α<sub>pLux</sub>/(γ<sub>AiiA</sub>+μ)</td>
| + | |
| - | <td class="row">0</td>
| + | |
| - | </tr>
| + | |
| - | </table>
| + | |
| - | </center>
| + | |
| - | <a name="Sensitivity analysis"></a>
| + | |
| - | <h2> <span class="mw-headline"> <b>Sensitivity analysis</b> </span></h2>
| + | |
| - | <p> Now, it is interesting to conduct some qualitative and quantitative considerations about our system sensitivity to its parameters and aTc input signal.</p>
| + | |
| - | <div> First of all, we analyze how the HSL output can be regulated by changing the characteristics of our RHs.</div>
| + | |
| - | <div>Referring to the first rectangular hyperbola, we recognize that its vertical asymptote could be varied by changing α<sub>p<sub>Lux</sub></sub></sub></sub> value (assuming fixed γ<sub>AiiA</sub> and μ). In particular, thanks to the four Plux-RBSx constructs realized, we can vary α<sub>p<sub>Lux</sub></sub></sub></sub> more than a hundred factor. This can significantly shift the vertical asymptote, bringing this first RH farther or nearer the second one (whose vertical asymptote is the ordinate axis), thereby providing an intersection at higher AiiA and lower HSL values, or vice versa. The following two figures highlight this aspect.</div>
| + | |
| - | <table align='center' width='100%'>
| + | |
| - | <div style='text-align:center'>
| + | |
| - | <div class="thumbinner" style="width: 100%;"><a href="File:Iperbole eq 3 as ver2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/4/45/Iperbole_eq_3_as_ver2.jpg" class="thumbimage" width="100%"></a></div>
| + | |
| - | </div>
| + | |
| - | </table>
| + | |
| - | <table align='center' width='100%'>
| + | |
| - | <div style='text-align:center'>
| + | |
| - | <div class="thumbinner" style="width: 100%;"> <a href="File:UNIPV inters RH ver alfa plux acceptable values2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/9/97/UNIPV_inters_RH_ver_alfa_plux_acceptable_values2.jpg" class="thumbimage" width="100%"></a></div>
| + | |
| - | </div>
| + | |
| - | </table>
| + | |
| - | <p>From the above figures, it is also clear that HSL steady state value is not very sensitive to α<sub>p<sub>Lux</sub></sub></sub></sub>, at least when this parameter presents values greater than unity, because this brings the two curves to intersect in their low slope regions.</p>
| + | |
| - | <p>Referring to the second RH, the only adjustable asymptote is the horizontal one, that we can move upward or downward by altering VLuxI, which indirectly depends on aTc.</p>
| + | |
| - | <table align='center' width='100%'>
| + | |
| - | <div style='text-align:center'>
| + | |
| - | <div class="thumbinner" style="width: 100%;"><a href="File:UNIPV RH2 eq2 as or corrected2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/0/04/UNIPV_RH2_eq2_as_or_corrected2.jpg" class="thumbimage" width="95%"></a></div>
| + | |
| - | </div>
| + | |
| - | </table>
| + | |
| - | <p>A further deepening in the exponential phase analysis involves determining the characteristics of the input-output relation. Our closed loop system can be realized with two alternative purposes in mind:</p>
| + | |
| - | <ol>
| + | |
| - | <li> realizing a circuit able to adapt HSL output depending on aTc input concentration. This requires a good sensitivity between input and output.</li>
| + | |
| - | <li> designing a robust HSL concentration controller, which is immune to the input noise and offers a constant and defined amount of HSL. In this case HSL level should be appropriately tuned during the design stage, by choosing the correct strength of promoter-RBSx complexes.</li>
| + | |
| - | </ol>
| + | |
| - | <p>Now,again considering the system of equations, it is easy to observe that HSL dependence on aTc input passes through two Hill equations. The former describes aTc driven LuxI synthesis, while the latter models LuxI dependent HSL synthesis rate. Therefore, in order to achieve a high aTc sensitivity, it is advisable to tune aTc and LuxI levels so that they place outside the saturation regions of their Hill curves. In this regard, it is possible to determine a closed form expression relating HSL to aTc, if we hypothesize that both aTc and LuxI are far lower than their respective half-saturation constant (k_ptet and Km), thus simplifying the Hills with a first order relation:</p>
| + | |
| - | <br>
| + | |
| - | <table align='center' width='100%'>
| + | |
| - | <div style='text-align:center'>
| + | |
| - | <div class="thumbinner" style="width: 100%;"><a href="File:UNIPV Sensitivity atc2.jpg" class="image"><img alt="" src="https://static.igem.org/mediawiki/2011/3/34/UNIPV_Sensitivity_atc2.jpg" class="thumbimage" width="75%"></a></div>
| + | |
| - | </div>
| + | |
| - | </table>
| + | |
| - | <a name="References"></a>
| + | |
| - | <h1><span class="mw-headline"> <b>References</b> </span></h1>
| + | |
| - | <div style='text-align:justify'>
| + | |
| - | <ol type='1'>
| + | |
| - | <a name="Braun">
| + | |
| - | <li>Braun D, Basu S, Weiss R (2005) <b>Parameter estimation for two synthetic gene networks: a case study </b> <i>ICASSP '05 </i> 5:v/769-v/772. </li>
| + | |
| - | <br>
| + | |
| - | <a name="Canton">
| + | |
| - | <li>Canton B, Labno A, Endy D. (2008) <b>Refinement and standardization of synthetic biological parts and devices. </b> <i> Nat Biotechnol. </i> 26(7):787-93. </li>
| + | |
| - | <br>
| + | |
| - | <a name="Danino">
| + | |
| - | <li>Danino T, Mondragón-Palomino O, Tsimring L et al. (2010) <b>A synchronized quorum of genetic clocks. </b> <i>Nature. </i> 463(7279):326-30. </li>
| + | |
| - | <br>
| + | |
| - | <a name="Endler">
| + | |
| - | <li>Endler L, Rodriguez N, Juty N et al. (2009) <b>Designing and encoding models for synthetic biology. </b> <i>J. R. Soc. Interface </i> 6:S405-S417. </li>
| + | |
| - | <br>
| + | |
| - | <a name="Kelly">
| + | |
| - | <li>Kelly JR, Rubin AJ, Davis JH et al. (2009) <b>Measuring the activity of BioBrick promoters using an in vivo reference standard.</b> <i> J. Biol. Eng.</i> 3:4.</li>
| + | |
| - | <br>
| + | |
| - | <a name="Pasotti">
| + | |
| - | <li>Pasotti L, Quattrocelli M, Galli D et al. (2011) <b>Multiplexing and demultiplexing logic functions for computing signal processing tasks in synthetic biology. </b> <i>Biotechnol. J. </i>6(7):784-95. </li>
| + | |
| - | <br>
| + | |
| - | <a name="Salis">
| + | |
| - | <li>Salis H M, Mirsky E A, Voight C A (2009)<b> Automated design of synthetic ribosome binding sites to control protein expression. </b> <i>Nat. Biotechnol.</i>27:946-950. </li>
| + | |
| - | <br>
| + | |
| - | </ol>
| + | |
| - | </div>
| + | |
| | </div> | | </div> |
| | + | </div> |
| | + | |
| | </html> | | </html> |
| | + | |
| | + | |
| | + | |
| | | | |
| | | | |
| | {{end}} | | {{end}} |







 "
"