Team:ETH Zurich/Modeling/Analysis
From 2011.igem.org
(→Coupled parameter variation) |
(→Protein Synthesis Rates) |
||
| (23 intermediate revisions not shown) | |||
| Line 7: | Line 7: | ||
= Parameter Sweeps = | = Parameter Sweeps = | ||
| - | For the parameters that belong to the band detector module, we explored their parameter spaces to quantify how they affect the features of the GFP band . As we varied each parameter (while keeping the rest constant), we varied also the acetaldehyde input and monitored the GFP output. We analyzed the parameter space only for the model that uses acetaldehyde as an input parameter. In both models the band is affected in the same way by the parameters of the band detector module. The sensor mechanism can only cause shifts in the band but the band detector module itself is unaffected by the input of the system. The parameter sweeps for the xylene model would therefore be similar to the acetaldehyde model, with differences only for the parameters involved in the sensor mechanism. <br><br> | + | For the parameters that belong to the band detector module, we '''explored their parameter spaces''' to quantify how they affect the features of the GFP band . As we varied each parameter (while keeping the rest constant), we varied also the acetaldehyde input and monitored the GFP output. We analyzed the parameter space only for the model that uses acetaldehyde as an input parameter. In both models the band is affected in the same way by the parameters of the band detector module. The sensor mechanism can only cause shifts in the band but the band detector module itself is unaffected by the input of the system. The parameter sweeps for the xylene model would therefore be similar to the acetaldehyde model, with differences only for the parameters involved in the sensor mechanism. <br><br> |
| - | In order to speed up the simulations, we derived the steady-state formulas in Maple for all the relevant species. In this way we were able to obtain the steady-state GFP value simply by knowing the input concentration of Acetaldehyde, without the need to use an ODE solver. Thus we were able to reduce the simulation time from about 30 minutes to under one minute for one parameter sweep. | + | In order to speed up the simulations, we '''derived the steady-state formulas''' in Maple for all the relevant species. In this way we were able to obtain the steady-state GFP value simply by knowing the input concentration of Acetaldehyde, without the need to use an ODE solver. Thus we were able to '''reduce the simulation time''' from about 30 minutes to under one minute for one parameter sweep. |
| Line 32: | Line 32: | ||
|- valign="top" | |- valign="top" | ||
| - | |[[File: | + | |[[File:ETHZ_LacI.png|thumb|460px|center|'''Figure 3''': Exploring the parameter space of LacI production rate]] |
|[[File:AlphaL2.png|thumb|400px|center|'''Figure 4''': Exploring the parameter space of LacI<sub>M1</sub> production rate]] | |[[File:AlphaL2.png|thumb|400px|center|'''Figure 4''': Exploring the parameter space of LacI<sub>M1</sub> production rate]] | ||
| Line 99: | Line 99: | ||
= Coupled parameter variation = | = Coupled parameter variation = | ||
| - | With doing the parameter sweeps for individual parameters, we saw how robust our system is with respect to a particular | + | With doing the parameter sweeps for individual parameters, we saw how robust our system is with respect to a particular parameter. But in reality, when parameters vary, they usually don't vary alone, but they are coupled (i.e more parameters vary simultaneously). One way to incorporate this fact in our model is to couple the expression rates of the proteins according to the plasmid they are expressed on and vary them together. <br><br> |
| - | We explored the coupled parameter space of TetR, CI and LacI production rates, by checking the GFP output as we varied the input acetaldehyde concentration. For the biological implementation of the SmoColi | + | We explored the coupled parameter space of TetR, CI and LacI production rates, by checking the GFP output as we varied the input acetaldehyde concentration. For the biological implementation of the SmoColi circuit, we constructed a three-plasmid system. On one of the plasmids (10-15 copies), TetR, CI and LacI were cloned. These are the proteins that play a crucial role in the band detector module and their production affects the characteristics of the GFP band. The copy number of the plasmid influences the amount of protein produced by the cell and plays an important role in our design, so we wanted to check what the band behaviour will be if we put these three genes on a different plasmid. We mimicked the variation of the plasmid copy number by varying the production rates of these 3 proteins simultaneously. <br><br> |
[[File:AlphaTCL.png|600px|thumb|center|'''Figure 14''': Exploring the coupled parameter space of TetR, CI and LacI production rates.]] | [[File:AlphaTCL.png|600px|thumb|center|'''Figure 14''': Exploring the coupled parameter space of TetR, CI and LacI production rates.]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | Figure 14 shows the coupled parameter space of the production rates of the three proteins. If none of these proteins is produced, LacI<sub>M1</sub> is free to repress GFP, so GFP is not produced either. As soon as these proteins start being produced, the circuit starts functioning normally and the band appears. For very low coupled production rates, it is very narrow and it starts widening as the production rates get higher. The surface of the parameter space combines the three different surfaces for production rates of TetR, CI and LacI separately. Even though the width and the position of the band slightly changes with the change of the production rates, its height stays constant, which means it is robust. Thus, even if we put these proteins on different copy number plasmids, our circuit will still function as we expect. However, for the purpose of smoke quantification, the optimal bandwidth corresponds to the placement of the genes on low copy number plasmids, since the narrow band can give more precise information about the input acetaldehyde concentration. | ||
{{:Team:ETH Zurich/Templates/SectionEnd}} | {{:Team:ETH Zurich/Templates/SectionEnd}} | ||
| Line 109: | Line 113: | ||
= Sensitivity Analysis = | = Sensitivity Analysis = | ||
| - | |||
Sensitivity analysis is a technique that studies the change of the output (or any observable) of a certain function with the variation of a certain parameter. It gives us an overview of how sensitive the model is with respect to the parameter, i.e. what the impact of the parameter is. The sensitivity is defined as the partial differential equation of the observable with respect to a certain parameter. | Sensitivity analysis is a technique that studies the change of the output (or any observable) of a certain function with the variation of a certain parameter. It gives us an overview of how sensitive the model is with respect to the parameter, i.e. what the impact of the parameter is. The sensitivity is defined as the partial differential equation of the observable with respect to a certain parameter. | ||
| Line 115: | Line 118: | ||
| - | [[File:sensitivity_steps_20.png|600px|thumb|center|'''Figure | + | [[File:sensitivity_steps_20.png|600px|thumb|center|'''Figure 15''': Sensitivity analysis with respect to acetaldehyde]] |
Latest revision as of 00:29, 29 October 2011
System Analysis
We wanted to analyse the effect of the parameters on the output of our system. We achieved this by looking at how the characteristics of the GFP band change when we explore the parameter space of a certain constant and at the sensitivity of GFP to the value of the toxic input substance (acetaldehyde or xylene).
Parameter Sweeps
For the parameters that belong to the band detector module, we explored their parameter spaces to quantify how they affect the features of the GFP band . As we varied each parameter (while keeping the rest constant), we varied also the acetaldehyde input and monitored the GFP output. We analyzed the parameter space only for the model that uses acetaldehyde as an input parameter. In both models the band is affected in the same way by the parameters of the band detector module. The sensor mechanism can only cause shifts in the band but the band detector module itself is unaffected by the input of the system. The parameter sweeps for the xylene model would therefore be similar to the acetaldehyde model, with differences only for the parameters involved in the sensor mechanism.
In order to speed up the simulations, we derived the steady-state formulas in Maple for all the relevant species. In this way we were able to obtain the steady-state GFP value simply by knowing the input concentration of Acetaldehyde, without the need to use an ODE solver. Thus we were able to reduce the simulation time from about 30 minutes to under one minute for one parameter sweep.
The following figures show how the band changes with the variation of protein production rates, repression coefficients and degradation rates.
Protein Synthesis Rates
|
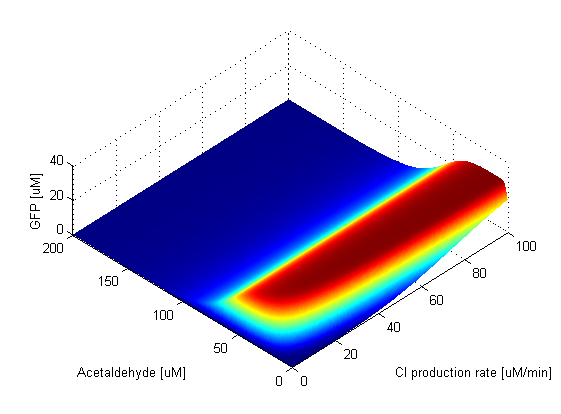
When the TetR production rate is zero, there is no TetR present in the cell, which means that LacIM1 is not repressed so it is free to block GFP production. This can be seen in the graph, since at this value of TetR production the band is absent. As soon as the production rate becomes non-zero, the band appears. The existence of the GFP band is not affected by the value of the TetR production rate, the band is present and the peak stays at a constant amplitude. TetR production rate only affects the width and position of the band which widens and shifts to higher acetaldehyde values as the production rate increases. When the CI production rate is zero, there is no CI present in the cell, which means that LacI is not repressed, so it is free to block the production of GFP. Thus, the band is absent at this value of CI production rate. After the CI production rate goes above a lower threshold, the band appears. We can observe that above the threshold the GFP band is very robust to the change in CI production rate, maintaining the position and amplitude of the peak at a constant value. The width of the band seems to slightly increase as the CI production rate increases, but at very high values it seems to stay constant. | ||
|
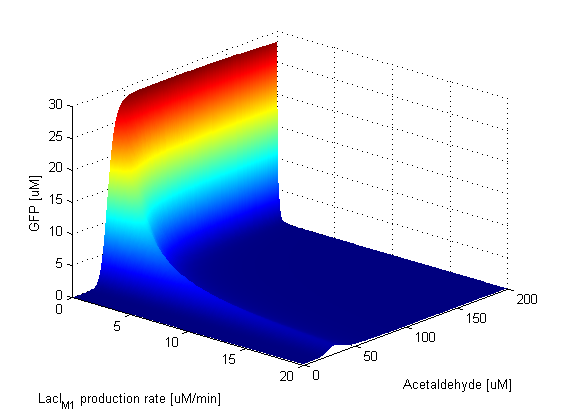
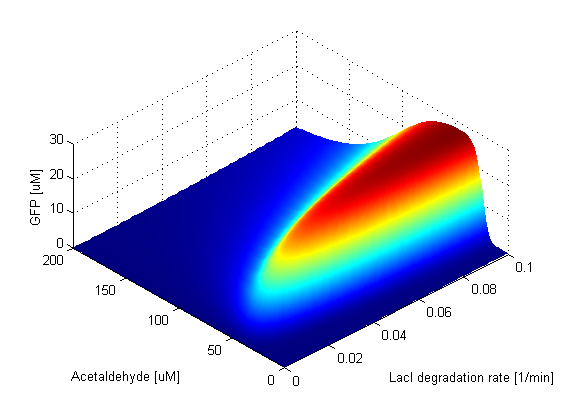
When the LacI production rate is zero, only the low-pass branch of the system is in function. This can be seen in the graph, as GFP is produced if Acetaldehyde has a concentration lower than 100 μM. However, as soon as LacI start being produced the band is formed. When the production rate of LacI gets too high, the amplitude of the band decreases, but the position of the peak and the width stay constant. | ||
|
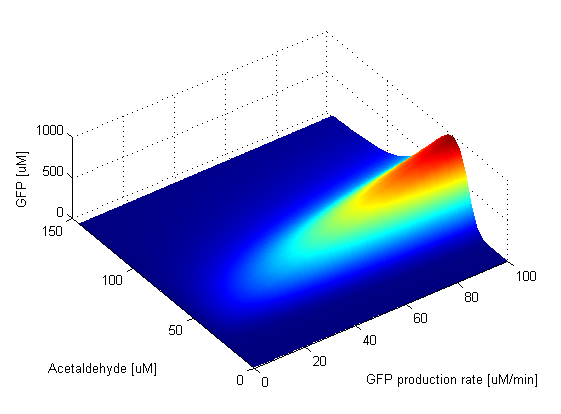
The GFP production rate has an effect only on the amplitude of the band. This is clear from the ODE of the GFP change in time. The amplitude of the GFP is thus directly proportional to the value of the GFP production rate. This can be seen in the graph. When the GFP production rate is zero, naturally no GFP molecules are produced. As soon as the production rate becomes nonzero, the band appears and its amplitude is increasing linearly with the value of the GFP production rate. The width of the band and position of the peak stay fixed. | ||
Repression Coefficients
|
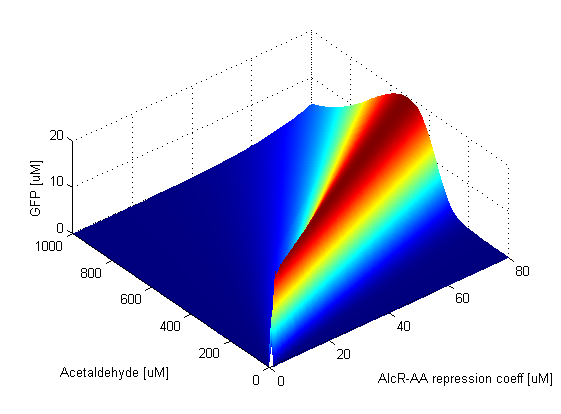
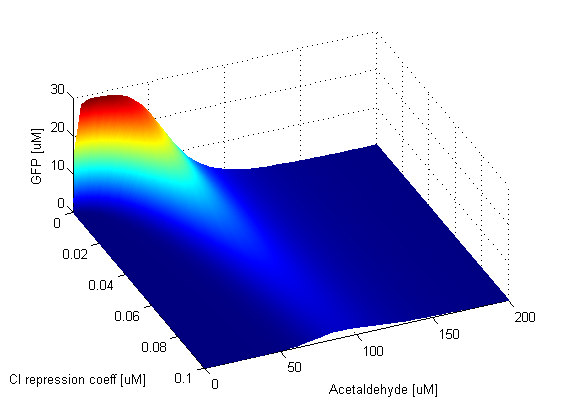
When the AlcR-AA repression coefficient is zero, TetR is always repressed. This in turn means that LacIM1 is always produced and it represses GFP production. Thus the band is absent. As soon as the AlcR-AA repression coefficient becomes nonzero, the band appears. Since when this value is low, repression of TetR is very efficient, the band is narrow. This can be clearly seen in the graph: the band widens and shifts the position of its peak to higher Acetaldehyde values as the repression becomes weaker. The AlcR-AA repression coefficient influences the lower and upper thresholds which determine where the band is positioned. The amplitude of the GFP band is not affected by the change of this parameter. When the TetR repression coefficient is zero, CI and LacIM1 are completely repressed, thus LacI is free to repress GFP and the band is absent. Since TetR is produced only when the Acetaldehyde concentration is low, if simultaneously the TetR repression coefficient is low, then GFP is repressed, however for higher Acetaldehyde concentrations GFP is produced. This is why in the graph we notice that for low TetR repression coefficients, above a certain Acetaldehyde concentration there is always GFP present. For high values of the TetR repression coefficient the opposite thing happens. GFP is produced for low Acetaldehyde concentrations because in this case repression of CI and LacIM1 is weak. Thus the TetR repression coefficient has an impact on the width and position of the band, but again the amplitude remains at the same value. | |
|
We observe that the GFP band is sensitive to the CI repression coefficent and appears only for low values of it. CI is responsible for repressing LacI, which in turn represses GFP. If the repression coefficient of CI is zero, LacI will never be produced so GFP is present. For low values of the CI repression coefficient the band will be present because even if there are very few CI molecules in the cell, they will still be able to repress LacI and produce GFP. As the value of the CI repression coefficient gets higher, repression of LacI gets weaker, so GFP is produced less and less. This is visible in the graph, as we can notice that the band is dissapearing for high values of the CI repression coefficient. The LacI repression coefficient direclty affects GFP production since GFP is repressed by LacI and LacIM1. When this repression coefficient has low values, GFP is always repressed by either LacI or LacIM1. For intermediate values, the band can be clearly distinguished. For high values of the LacI repression coefficient, the repression of GFP is very weak, so even for high Acetaldehyde concentrations where LacIM1 should repress GFP, this does not completely happen and we get leaky GFP production. | |
Protein Degradation Rates
|
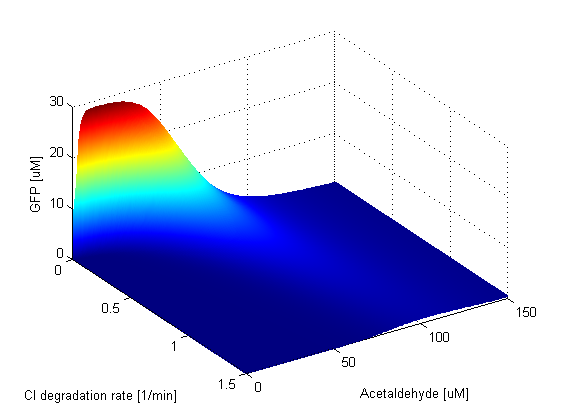
TetR production is high when the Acetaldehyde concentration is below 20 μM. If the TetR degradation rate is very low, the GFP band appears at higher Acetaldehyde concentrations and it shifts towards lower Acetaldehyde concentration as the TetR degradation rate increases. The amplitude of the band is unaffected however. When the TetR degradation rate is very high, TetR is degraded almost instantly after it is produced, meaning that TetR is almost always absent in the cell. Thus LacIM1 is free to repress GFP and the band dissapears. The branch that includes CI should repress GFP when the Acetaldehyde concentration is low, that is when TetR concentration is high. When the CI degradation rate is low, CI is able to repress LacI to allow the band to form. However, when the CI degradation rate gets higher, there are too few CI molecules in the cell, and they are not able to repress LacI. This is the reason why at these values of the degradation rate the band is dissapearing. | |
|
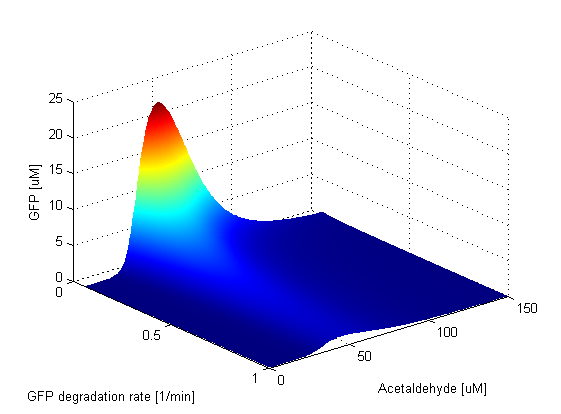
LacI and LacIM1 direclty repress GFP. We notice that the amplitude of the GFP peak and the bandwidth exhibit positive correlation with respect to the LacI degradation rate. This is due to the fact that as the degradaton rate increases, there are fewer LacI and LacIM1 molecules in the cell and thus more GFP will be produced. As expected, there is a strong negative correlation between the height and width of the peak and the GFP degradation rate. This is due to the fact that the GFP band can exist only if the GFP molecules are not degraded too quickly. | |
Coupled parameter variation
With doing the parameter sweeps for individual parameters, we saw how robust our system is with respect to a particular parameter. But in reality, when parameters vary, they usually don't vary alone, but they are coupled (i.e more parameters vary simultaneously). One way to incorporate this fact in our model is to couple the expression rates of the proteins according to the plasmid they are expressed on and vary them together.
We explored the coupled parameter space of TetR, CI and LacI production rates, by checking the GFP output as we varied the input acetaldehyde concentration. For the biological implementation of the SmoColi circuit, we constructed a three-plasmid system. On one of the plasmids (10-15 copies), TetR, CI and LacI were cloned. These are the proteins that play a crucial role in the band detector module and their production affects the characteristics of the GFP band. The copy number of the plasmid influences the amount of protein produced by the cell and plays an important role in our design, so we wanted to check what the band behaviour will be if we put these three genes on a different plasmid. We mimicked the variation of the plasmid copy number by varying the production rates of these 3 proteins simultaneously.
Figure 14 shows the coupled parameter space of the production rates of the three proteins. If none of these proteins is produced, LacIM1 is free to repress GFP, so GFP is not produced either. As soon as these proteins start being produced, the circuit starts functioning normally and the band appears. For very low coupled production rates, it is very narrow and it starts widening as the production rates get higher. The surface of the parameter space combines the three different surfaces for production rates of TetR, CI and LacI separately. Even though the width and the position of the band slightly changes with the change of the production rates, its height stays constant, which means it is robust. Thus, even if we put these proteins on different copy number plasmids, our circuit will still function as we expect. However, for the purpose of smoke quantification, the optimal bandwidth corresponds to the placement of the genes on low copy number plasmids, since the narrow band can give more precise information about the input acetaldehyde concentration.
Sensitivity Analysis
Sensitivity analysis is a technique that studies the change of the output (or any observable) of a certain function with the variation of a certain parameter. It gives us an overview of how sensitive the model is with respect to the parameter, i.e. what the impact of the parameter is. The sensitivity is defined as the partial differential equation of the observable with respect to a certain parameter.
We performed sensitivity analysis with respect to acetaldehyde or xylene. For different input concentrations we monitored the change in the GFP output (dGFP/dAcetaldehyde or dGFP/dXylene).
For the acetaldehyde model, it can be seen from the above figure that the sensitivity is highest when GFP rises. For the peak itself (at [AA] = 1000uM), the sensitivity drops down and then rises again once GFP concentration starts decreasing. This tells us that the GFP concentration level is most sensitive to acetaldehyde at those concentrations where GFP rises and falls.
 "
"