Stochastic Analysis

Besides the parameter space search, we performed another type of analysis in order to verify that our system is robust and that it is not bistable. We were especially interested in the GFP band, whether it is always present and whether the amount of GFP produced in the cells for different concentrations of Acetaldehyde has large fluctuations. Because gene expression is an intrinsically stochastic process, we performed stochastic simulations to see how our system reacts to noise and how it responds to perturbations.

The following results show that our system is indeed robust and it does not have bifurcations.

Method

For the stochastic simulations we used the [http://magnet.systemsbiology.net/software/Dizzy/ Dizzy] software, to which we gave as an input an SBML file with the description of our system. Moving from deterministic to stochastic simulations we had to change several things in the SBML file. Firstly, we exported the SBML file to a CMDL format.Next, we converted the species values as well as the production rates and repression coefficients from concetrations (in μM) to numbers of molecules. Since our initial system was described in terms of ODEs, we also had to change this by separating the system into distinct reaction channels (i.e. separate degradation from activation/repression) and specifying the reaction rates.

With the new description of the system, we could start the simulations. For analyzing the robustness of the system, we chose 5 strategic Acetaldehyde concentrations (see Figure 1), and for each of them we performed stochastic simulations. We selected the following Acetaldehyde concentrations:

• 0 μM (0 molecules). At this concentration the GFP output should approach 0 μM.
• 25 μM (30110 molecules). At this concentration GFP rises quickly, so it should be very sensitive to noise.
• 46 μM (55402 molecules). This is the concentration that gives the peak GFP value.
• 100 μM (120440 molecules). At this concentration GFP is decreasing, so it should be sensitive to noise.
• 300 μM (361320 molecules). At this concentration the GFP output should again approach 0 μM.

Figure 1: GFP versus Acetaldehyde. The red squares denote the 5 Acetaldehyde concentrations for which we simulated the time course of GFP steady state in stochastic mode.

In order to be sure that we are indeed simulating the time course of the stochastic steady state, and that we are not in the transient regime, we implemented the following approach:

• We ran a deterministic simulation for 5000 minutes (~ 83 hours) to get to the deterministic steady state. We took over the concentration values for the last time point as new initial conditions for the next simulation.
• We ran a stochastic simulation for 10000 minutes (~ 7 days), to make sure that we are somewhere around the “stochastic steady state”. Once again we took over the concentration values for the last time point as new initial conditions for the next simulation.
• We ran a long stochastic simulation for 100000 minutes (~ 70 days) taking samples every minute.

Simulations

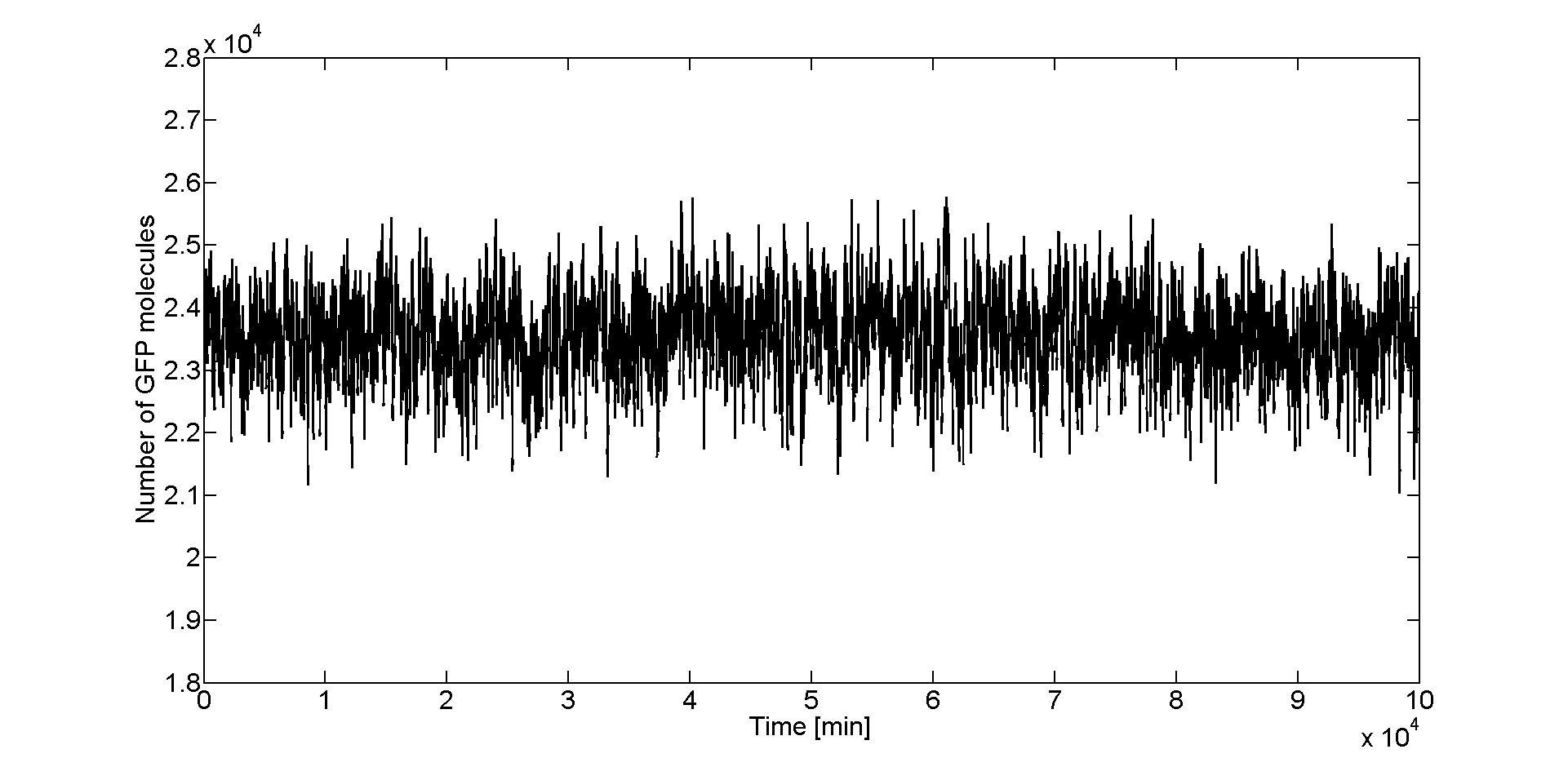
After we obtained the samples with Dizzy, we loaded the data in Matlab to analyze it. To get an initial feeling of how the system behaves in the stochastic regime, we plotted the GFP molecule numbers fucntion of time. In Figure 2 we can see that for the peak of the band (Acetaldehyde = 46 μM), GFP values fluctuate around a steady state which is about 23500 molecules.

Figure 2: Stochastic simulation of GFP steady state for an Acetaldehyde concentration of 46 μM.

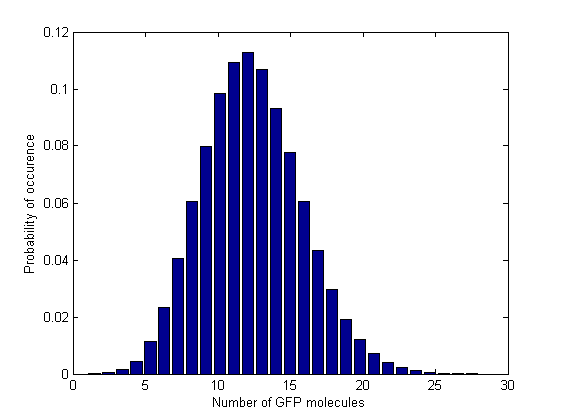
Next, in order to see how the values are distributed and whether there are multiple steady states, we plotted the normalized histograms for the 5 data sets. We used 150 bins for plotting the histograms for the 3 intermediate Acetaldehyde values and 28, respectively 61 bins for the first and last Acetaldehyde value. In these last 2 cases we had to reduce the number of bins becasue the range of the GFP molecule values was narrower.

Figure 3: Distribution of the number of GFP molecules for an Acetaldehyde input of 0 μM	Figure 4: Distribution of the number of GFP molecules for an Acetaldehyde input of 25 μM
Figure 5: Distribution of the number of GFP molecules for an Acetaldehyde input of 46 μM	Figure 6: Distribution of the number of GFP molecules for an Acetaldehyde input of 100 μM

Figure 7: Distribution of the number of GFP molecules for an Acetaldehyde input of 300 μM

Analysis of Results

From the time course plot (Figure 2) we can already see that the values always fluctuate around one steady state which leads us to believe that the system is stable. Since the numbers of GFP molecules do not jump between two or more distinct values we can assume that the system is not bistable. The plot alone however does not constitute conclusive evidence, so for this reason we generated and analyzed the distributions of GFP values.