Team:ETH Zurich/Modeling/Analysis
From 2011.igem.org
(→Protein Synthesis Rates) |
(→Protein Synthesis Rates) |
||
| Line 53: | Line 53: | ||
|- | |- | ||
|colspan="2"| | |colspan="2"| | ||
| - | + | ||
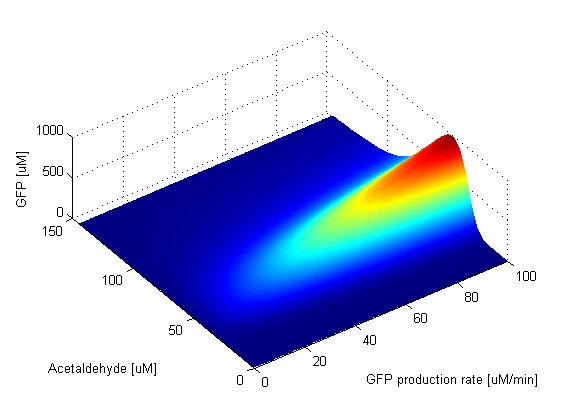
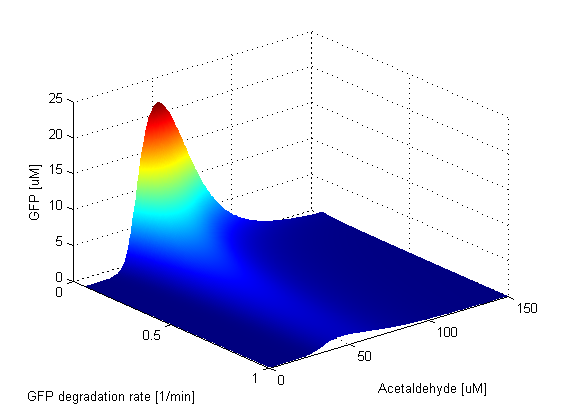
| + | The GFP production rate has an effect only on the amplitude of the band. This is clear from the ODE of the GFP change in time. The amplitude of the GFP is thus directly proportional to the value of the GFP production rate. This can be seen in the graph. When the GFP production rate is zero, naturally no GFP molecules are produced. As soon as the production rate becomes nonzero, the band appears and its amplitude is increasing linearly with the value of the GFP production rate. The width of the band and position of the peak stay fixed. | ||
| | | | ||
|} | |} | ||
Revision as of 11:09, 24 October 2011
| System Analysis |
| ||
| We wanted to analyse the effect of the parameters on the output of our system. We achieved this by looking at how the characteristics of the GFP band change when we explore the parameter space of a certain constant and at the sensitivity of GFP to the value of the toxic input substance (acetaldehyde or xylene) . | |||
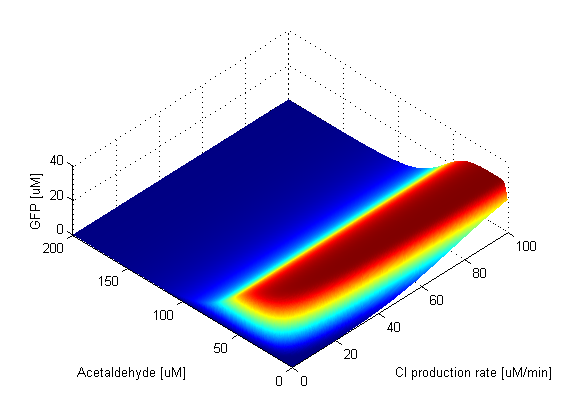
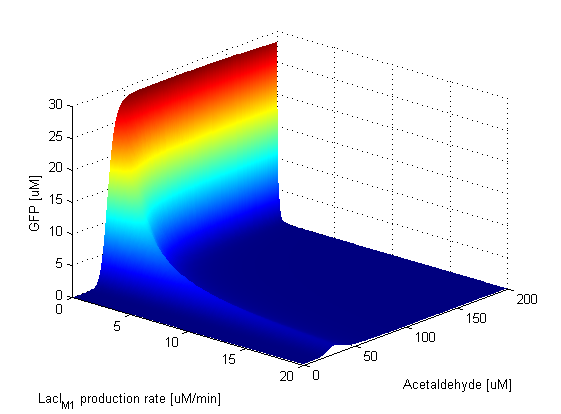
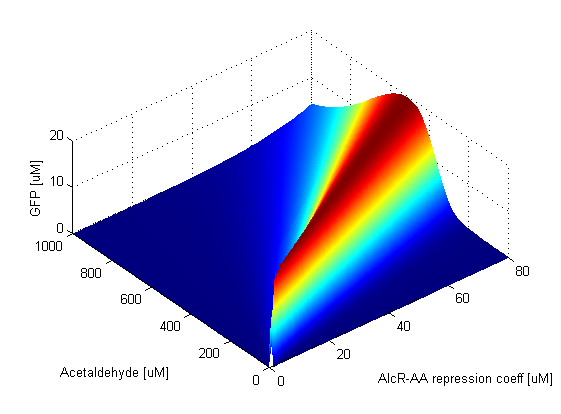
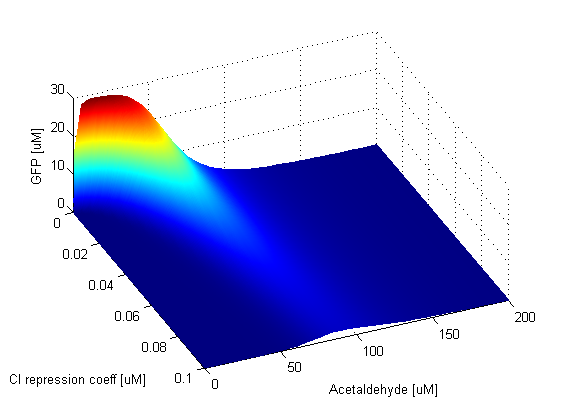
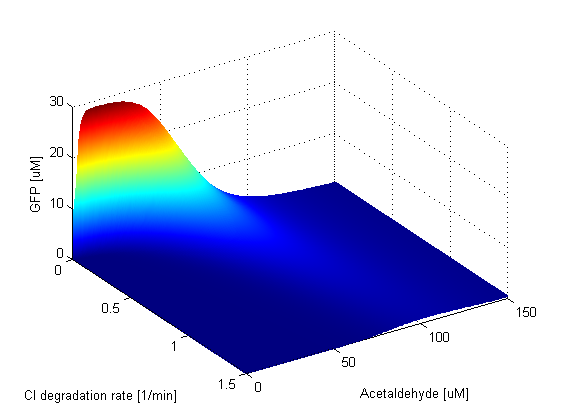
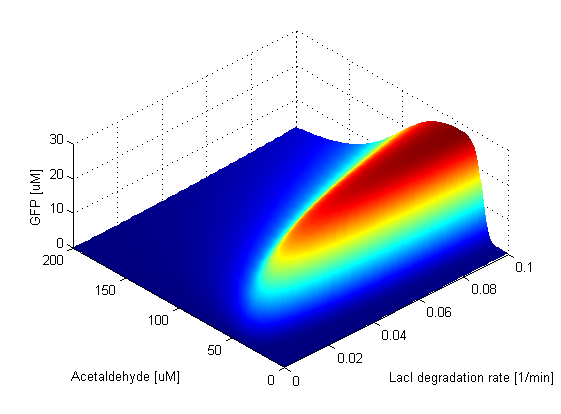
Parameter SweepsFor the parameters that belong to the band detector module, we explored their parameter spaces to quantify how they affect the features of the GFP band . As we varied each parameter (while keeping the rest constant), we varied also the acetaldehyde input and monitored the GFP output. We analyzed the parameter space only for the model that uses acetaldehyde as an input parameter. In both models the band is affected in the same way by the parameters of the band detector module. The sensor mechanism can only cause shifts in the band but the band detector module itself is unaffected by the input of the system. The parameter sweeps for the xylene model would therefore be similar to the acetaldehyde model, with differences only for the parameters involved in the sensor mechanism. In order to speed up the simulations, we used Maple to derive the steady-state formulas for all the relevant species. In this way we were able to obtain the steady-state GFP value simply by knowing the input concentration of Acetaldehyde, without the need to use an ODE solver. Thus we were able to reduce the simulation time from about 30 minutes to under one minute for one parameter sweep. The following figures show how the band changes with the variation of protein production rates, repression coefficients and degradation rates.
Protein Synthesis Rates
Repression Coefficients
Protein Degradation Rates
| ||||||||||||||||||||||||||||
Coupled parameter variationWith doing the parameter sweeps for individual parameters, we saw how robust our system is with respect to a particular paramter. But in reality, when parameters vary, they usually don't vary alone, but they are coupled (i.e more parameters vary simultaneously). One way to incorporate this fact in our model is to couple the expression rates of the proteins according to the plasmid they are expressed on and vary them together. |
hji |
Sensitivity AnalysisSensitivity analysis is a technique that studies the change of the output (or any observable) of a certain function with the variation of a certain parameter. It gives us an overview of how sensitive the model is with respect to the parameter, i.e. what the impact of the parameter is. The sensitivity is defined as the partial differential equation of the observable with respect to a certain parameter. We performed sensitivity analysis with respect to acetaldehyde or xylene. For different input concentrations we monitored the change in the GFP output (dGFP/dAcetaldehyde or dGFP/dXylene).
|
 "
"