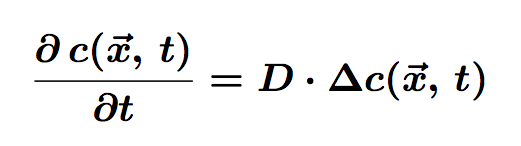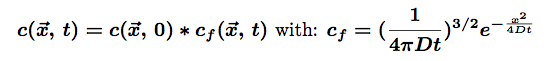Team:Paris Bettencourt/Modeling
From 2011.igem.org

Contents |
Modeling introduction
What is modeling in synthetic biology?
Synthetic biology relies heavily on genetic constructs designed to perform a specific task. In order to predict the behaviour of such systems, we need to be able to model it. Knowing in advance how well or how poorly a construct will work can help us during the genetic design phase or when we need to prepare our experiments. We need to describe the future reactions of our system is to create a mathematical model of it.
The bible for synthetic biology modeling is Uri Alon's book An Introduction to Systems Biology: Design Principles of Biological Circuits. Most of our models are based on his approach to biological circuits. We are now going to explain quickly what is the basic structure behind our simulations.
The gene geneX is responsible for the production of the corresponding protein X. The promoter pX controlling the expression geneX can be:
- A constitutive promoter, geneX is activated whatever the conditions
- Positively regulated, geneX is more active when an inducer is present
- Negatively regulated, geneX is less active when an repressor is present

The inducer or repressor can be another protein or even the product itself. In the latter case, the gene is auto-regulated, wether positively or negatively. To begin, let's assume pX is a constitutive promoter for now. We will make another simplification by taking into account the translation step and assuming that the gene "directly" produces protein X.
We will know take a look at the parameters involved in modeling this network.
X is the concentration of protein X alpha is the expression rate of protein X (molecule.s^-1). It mainly depends on the constitutive promoter. delta_dil is the dilution rate, due to cell division (s^-1) delta_deg is the degradation rate of protein X
The equation and solution modeling the behaviour of this system are the following:
INSERT IMAGE HERE (initial conditions zero)
Now, let's assume that pX is auto-regulated, either positively or negatively. We need to introduce a few new parameters.
K is the dissociation constant, representing the binding of a inducer/repressor to the promoter n is the Hill coefficient of the function beta is the maximum production rate of our gene (molecule.s^-1) alpha now represents the basal expression ("leaking") of the gene (molecule.s^-)
The equations and solutions are now:
INSERT IMAGE HERE (initial conditions zero, parameters noted)
You will note that the regulation is modeled as a Hill function. This type of functioncan help us model most of the regulation that takes place in a genetic network.
Of course most genetic networks are more complex than simply auto-regulated nodes. The product of one gene can regulated the activation of another which in turn inhibits a third, etc. By coupling this kind of equations together, we achieved modeling most of our genetic networks pretty easily.
Our choices for modeling
Translation
We introduced the translation step in our models. This means each equation described aboved is transformed into two equations: one describing mRNA production and one describing the translation of this mRNA into a protein. We then need to introduce the protein production rate gamma. The equations are now:
INSERT DOUBLE EQUATION
This is justified notably because of our tRNA construction. This design relies directly on the translation process, we therefore need to model it if we want to compare models for different designs.
Delays for maturation
We also introduced a delay for protein production and maturation. Most models can ignore this but our experiments rely heavily on time measurement which means that for proteins with maturation time around 5 min (to compare with the cell division time 40 min) we need to take this into account. We chose to model this simply by adding a delay to the response time as it is shown in the following equations:
INSERT IMAGE HERE
No delays for diffusion in receptor cell
Most of our designs rely on the following scheme: a emitter cells creates a signaling protein which is received through the nanotubes by a receiver cell whuch is then activated. However, one could argue that after entering the receiver cell, the signaling proteins spend a significant time diffusing in it before reaching the receptor gene construct. we discussed this at length before finally agreeing not to consider this as a delay.
Several models showed us that diffusion, even of a single signaling molecule, happen too fast to add any delay to the response time of the system. We will discuss two of these models here.
Using diffusion equations
The first step is to study the general principles of diffusion and to apply them to a single molecule. We expected to estimate the order of magnitude for diffusion time of molecules with this model, not to have a precise understanding of the movement of molecules in a cell. Most of our experimental designs rely on time measurement to characterize the nanotubes, it was therefore crucial to see if diffusion time could add a significant delay to the response of receiver cells.
The principle of this model is quite simple. We use the statistical diffusion equation with a new normalisation constant so that it describes the behaviour of one molecule. Rather than obtaining a concentration field, we end up with a distribution of the density of probability to find the molecule at a certain position and a certain time. We did not use any kind of boundary conditions, we therefore only model the "movements" of one molecule floating in an infinite water medium.
The equation of diffusion is the following:
Where c is the concentration of particles in the cell, function of <math>\vec{x}</math> (position) and t (time). D is the diffusion coefficient.
The solution for such an equation is:
The star * represents the convolution of the two functions. The first part represents the initial conditions which are in our case a Dirac function centered on the origin of space (there is only one molecule at (0,0,0) at t=0). the second part of this solution is the so-called fundamental solution.
The solution can be re-written then:
INSERT SOLUTION HERE
This solution shows that through time, the density of probability "diffuses" in all directions equally. We can therefore think in 1 dimension since all directions behave in the same way, provided we keep the same origin.
INSERT PROBABILITY DIFFUSION IN 3D AND 1D HERE
What is of interest for us is the instant when we can consider that the probability of the presence of the molecule is "the same" for every point in the cell. The cell here is an arbitrary boundary which has no direct impact on the model. In our approach, the cell is a sphere centered on the origin and with a diameter of 1 micrometer (roughly Subtilis length). We chose to consider that the probability is "the same" when the lowest probability within the cell is 95% of the highest probability in the cell (ie in the center).
INSERT PROBABILITY DIFFUSION IN 1D WITH CELL BOUNDARY + 95% LIMIT
We can then solve analytically the equation:
INSERT RESOLUTION
We therefore see that the particle diffusing could be anywhere in the cell a mere XX s after entering the cell. This is too small to be mesured acurately through any biological reporter.
Using a stochastic model
This model is very similar to the one used in [Ribosome kinetics and aa-tRNA competition determine rate and fidelity of peptide synthesis. Fluitt A, Pienaar E, Viljoen H. Comput Biol Chem. 2007 Oct;31(5-6):335-46. Epub 2007 Aug 15.]. We consider that the particle diffusing in the cell is a random walker.
We want to see how long it takes for a particle of a given size to diffuse to any point of a cell. We use the following parameters: V volume of the cell (10^-18 m^3) lambda characteristic size of the particle (m) D diffusion coefficient of the particle (m^2.s^-1)
We divide the cytoplasm volume V into N= V/lambda^3 occupation sites for the walker. The characteristic time tau associated with the transition from one site to another is: tau=lambda^2/(6*D) [1]
If we have R walkers of this type, the probability that a molecule arrives at a given occupation site during the time interval tau is: p=R/N. In our case we study only one molecule (worst case scenario) so let us assume R=1.
The average time that elpases before the arrival of a particle is: t=tau/p=N*tau=V/(6*lambda'*D).
You will find below a table of time before arrival for different molecules.
INSERT TABLE.
Parameters
Finally, we made some assumptions for certain parameters that are used in most our models. These assumptions are discussed at length in the Parameters section.
ADD LINK
Direct observation
Characterization
T7 system
tRNA_amber system
Distribution of tRNA_amber in mRNA populations
Master/Slave
Bi-directional communication
 "
"