Team:Paris Bettencourt/Modeling/tRNA distribution

• Home
• Presentation
  • Overview
  • Potential applications
  • Collaborations
  • The team
  • Acknowledgements →
    • Host laboratory
    • Sponsors
• Designs
  • Designs overview & concepts
  • Designs list
• Modeling
  • General overview
  • Modeling results for our designs →
    • The basics
    • Our assumptions
    • T7 polymerase diffusion
    • tRNA diffusion
    • ComK/ComS system
    • Parameters
  • Results of our passive diffusion model
  • Toward assisted diffusion
• Data
• Results
  • Achievements
  • Methodologies →
    • Microscopy
    • Micro-fluidic
    • Integration in B.subtilis
    • Kinetics
  • Parts list
  • Notebook
• Human practice & Safety
  • Human practice
  • Safety
  • Brainstorming
  • Bonus track

We have defined two models for this system which both rely on the following assumptions :

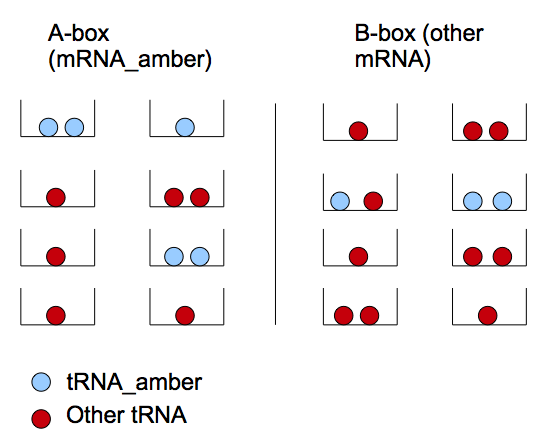
• Each mRNA is defined as a 'box'
• All the tRNA molecules are uniformly distributed in the boxes.
• The number of tRNA_amber diffused through the nanotubes is much more smaller than the one of the mRNA. Thus the chance that three or more tRNA amber will "find" one mRNA-T7 is negligible comparing to the one of two tRNA amber (finding a mRNA-T7). In our model we will consider that at one moment of time each mRNA interacts with 0, 1 or 2 tRNA ambers.
• The tRNA_amber placed in a correct box are always used

Let's define two types of boxes: mRNA_amber ('A') and other type of mRNA ('B'). We note the mRNA_amber producing T7 as mRNA*_amber. The latter appears if we have two tRNA_amber in one box. This model treats the repartition of tRNA_amber in the different boxes.

We note P(x) the probability of having x A-boxes containing two tRNA_amber. Thus P(x=1) corresponds to the probability of finding a couple of tRNA_amber in an A-box, thus to produce x T7 molecules. 't' is the number of tRNA_amber in the cell.

We note:

• P(x=1)= (probability that 2 balls choose A-boxes) * (probability that these 2 balls choose the same A-box) + (probability that 3 balls choose A boxes) * (probability that 2 balls out of 3 choose the same A-box and the third doesn't) + ... + (probability that t balls choose an A-box) * (probability that 2 of these t balls choose the same A-box and the rest don't).

• P(x=2)= (probability that 4 balls choose A-boxes) * (probability that these 4 balls choose 2 A-boxes, one A-box per pair of balls) + (probability that 5 balls choose A-boxes) * (probability that 4 balls out of 5 choose 2 A-boxes, one A-box per pair of balls and the fifth doesn't) + ... + (probability that t balls choose A-boxes) * (probability that 4 out of these t balls choose [t/2] A-boxes, one A-box per pair of balls and the rest don't).

• ...

• P(x=i)= (probability that 2i balls choose A-boxes) * (probability that these 2i balls choose i A-boxes, one A-box per pair of balls) + (probability that (2i + 1) balls choose A-boxes) * (probability that 2i balls out of (2i + 1) choose i A-boxes, one A-box per pair of balls and the rest don't) + ... + (probability that t balls choose A-boxes) * (probability that 2i out of these t balls choose [t/2] A-boxes, one A-box per pair of balls and the rest don't).

Hence: