Team:Edinburgh/Cellulases (Kappa model)

Cellulases (Kappa model)

Kappa

Kappa is a stochastic, agent-based language for simulating interactions in (mostly) biological systems. It has been used by several iGEM teams before, most notably by Team Edinburgh 2010, who used it to develop a model awarded the Best Model Prize.

Advantages of Kappa:

• easy to learn - you can summarise the syntax of the whole language on one page
• no need for knowing mathematical formulae (ODEs) - the sophisticated code simulates the system based on rules instead
• the models are relatively easy and quick to develop, and easily scalable by connecting more models into one
• there exist some graphical tools to aid creation of models - e.g. [http://www.rulebase.org/ RuleBase]

Kappa represents the world in terms of agents. Agents in Kappa can have states, and can be linked to one another by bonds. Reactions are represented as creation/deletion of agents/bonds.

For example, the reaction of a bound enzyme producing two end products would look like that:

Enzyme(activeSite!1), Substrate(enyzmeBindingSite!1) ->
                                          Enzyme(activeSite), Product1(), Product2()

Structure of the model

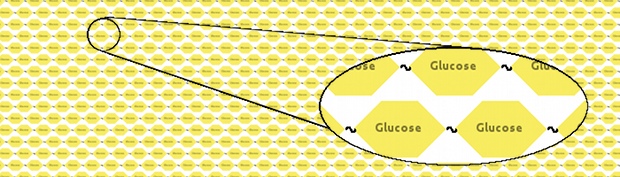
We thought that a neat model would represent cellulose as a long fibre of glucoses linked together:

Cellulose represented as long fibres of glucose

However, manually inputting that would be a considerable effort. Instead, we made a Kappa system which would build cellulose for us, and then, using Kappa syntax, took a snapshot of the model. Two variants were created, one with long (10,000 glucoses) fibres of cellulose and another one with short (1,000 glucoses) fibres.

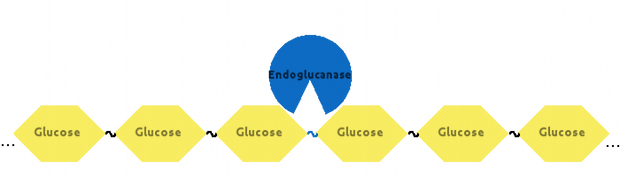
Then, Endoglucanase would cut Cellulose somewhere in the middle:

Endoglucanase digests cellulose chains

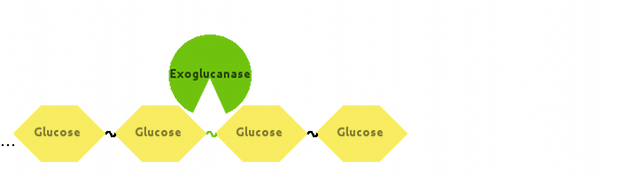
Also, Exoglucanase would cut Cellulose at end-points:

Exoglucanase digests cellulose chains

[http://dx.doi.org/10.1146/annurev-biochem-091208-085603 Fontes and Gilbert (2010)] have suggested that Exoglucanase is inhibited by its end product - Cellobiose, so we modelled that interaction as well.

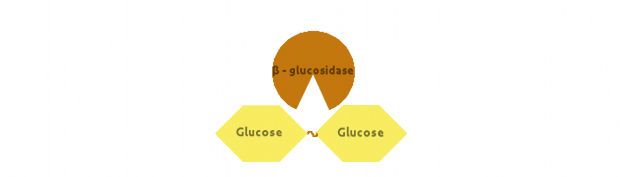
Finally, β-glucosidase would cut dimers (i.e. Cellobiose):

β-glucosidase digests cellobiose

We also modelled end-product inhibition of β-glucosidase by glucose.

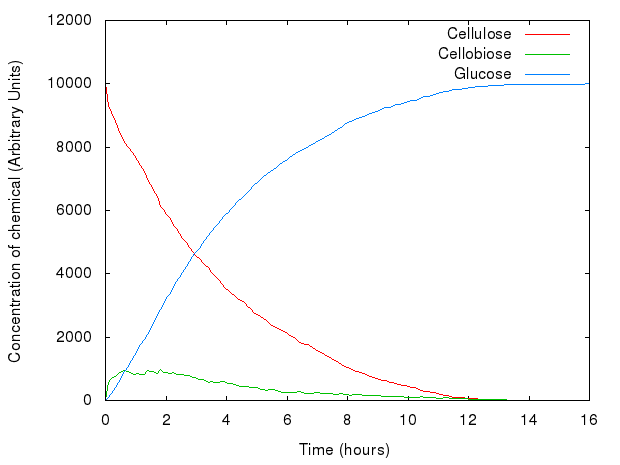
Non-synergistic model

We developed our first, non-synergistic model in Kappa, based on the system as seen above. We carried out a series of experiments in order to fit parameters to our model. The aim was to generate graphs similar to those in Kadam, Rydholm & McMillan (2004) (since back then we did not have any data available from the wet lab). We manipulated the kinetic rates of reactions and relative concentrations of enzymes.

After an overnight series of experiments using a computing cluster in the [http://www.inf.ed.ac.uk School of Informatics], we came up with a set of values for parameters of our model.

Experimentally fixed reaction rates

You can download the ready model as a .zip file:

Synergy model

Since Kappa models can be easily extended (by adding new agents, or reaction rules), we tried to make a synergistic model based on the non-synergistic model.

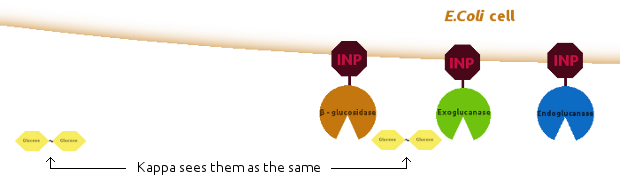
We introduced new agents: an E.Coli cell and several copies of INP, to be linked together as shown below:

A diagram of the synergistic (yet non-spatial) model.

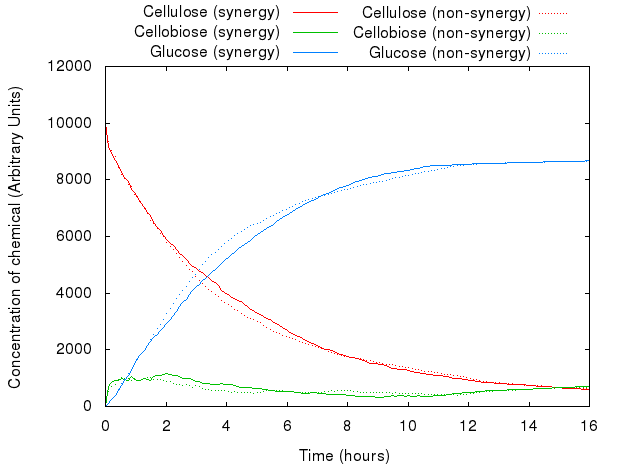
However, that did not act as we predicted. The following graph presents both models.

A graph showing the output of both synergy and non-synergy models. Dotted lines indicate the non-synergistic model

The graph above shows that for the same set of parameters, there is virtually no difference between the two systems. This is because Kappa does not have the notion of proximity, i.e. the simulator has no way of distinguishing between the products of enzymes produced just a second ago and the ones floating far away in the solution:

A diagram showing two cellobiose molecules, one close to the enzymes, and one far away in the solution. However, Kappa simulator does not distinguish between them.

Spatial Kappa

[http://www.demonsoft.org/SpatialKappa/ Spatial Kappa] is an extension to Kappa made by our last year's team (Team Edinburgh 2010). It seems like the extra functionality of compartments added by Spatial Kappa would help develop a model of synergistic action.

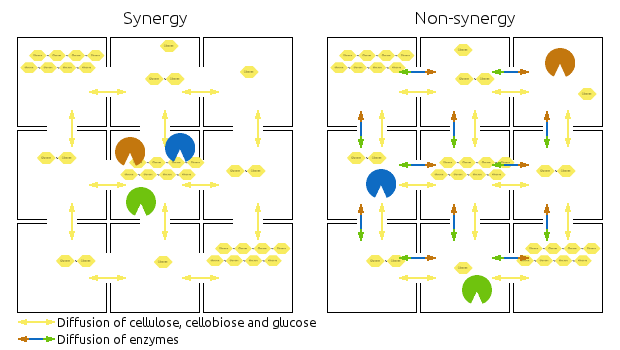
Our model could work in the following way:

• In the synergistic system, the enzymes are all in one compartment, meaning that the end-products will be available to the enzymes. The products and substrates would be allowed to diffuse across compartments, while the enzymes would not.
• The non-synergistic system would be very similar, but the enzymes could diffuse across compartments.

Because of the design choice we made at the beginning - representing cellulose as a chain of glucoses - we encountered a problem while setting up diffusion rules. It is trivial to set up diffusion rules for enzymes (just one rule per enzyme), but for the diffusion of cellulose, we would need to set up a separate rule for every possible length of cellulose chain - in our case that would amount to 1000 rules. While it is possible to automatically generate that (e.g. using Python), this will would slow the model down, meaning it would become intractable.

Therefore we tried a different representation of cellulose, where the agent Cellulose has a length n,

n ∈ {1..10}

(representing a chain of cellulose of length 2ⁿ⁺¹ glucoses).Then,

• Endoglucanase would take a chain of length n, and produce two chains of length n-1 (or two cellobioses from a chain of length 1);
• Exoglucanase would take a chain of length n, and produce n-1 chains of decreasing length, connected to each other, plus an extra chain of length n = 1, plus a particle of Cellobiose, thus conserving the amount of glucose:

2n+1 = 2n + 2n-1 + … + 23 + 22 + 2 + 2

• Endoglucanase could then split chains made in Exoglucanase reaction;
• β-glucosidase would split Cellobiose into two glucoses;
• β-glucosidase is inhibited by its end-product, glucose;
• Exogluconase is inhibited by cellobiose.

A diagram of the spatial model.
Left side shows then non-synergistic model, the synergistic model is shown in the right.
Note that the amounts of enzymes and substrates is identical in both models.

TODO: Synergy - enzymes don't move. Non-Synergy - enzymes move around.

References

• Fontes CMGA, Gilbert HJ (2010) [http://www.annualreviews.org/doi/abs/10.1146/annurev-biochem-091208-085603 Cellulosomes: highly efficient nanomachines designed to deconstruct plant cell wall complex carbohydrates]. Annual Review of Biochemistry 79: 655-81 (doi: 10.1146/annurev-biochem-091208-085603).
• Kadam KL, Rydholm EC, McMillan JD (2004) [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Development and validation of a kinetic model for enzymatic saccharification of lignocellulosic biomass]. Biotechnology Progress 20(3): 698–705 (doi: 10.1021/bp034316x).