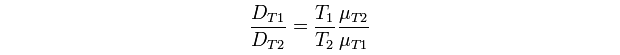Team:Edinburgh/Model Comparison
From 2011.igem.org
(→Flexibility) |
(→Flexibility) |
||
| Line 21: | Line 21: | ||
We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme. | We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme. | ||
| - | *Temperature | + | *'''Temperature''' |
| - | **MATLAB - Very flexible | + | **MATLAB - Very flexible as it incorporates the Arrhenius law which models the temperature-dependent reaction rate constant. |
**Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:<br/>[[File:Edinburgh-Stokes-Einstein.png|thumb|center|620px|T<sub>1</sub> and T<sub>2</sub> denote temperatures 1 and 2, respectively<br /> | **Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:<br/>[[File:Edinburgh-Stokes-Einstein.png|thumb|center|620px|T<sub>1</sub> and T<sub>2</sub> denote temperatures 1 and 2, respectively<br /> | ||
D is the diffusion coefficient (cm<sup>2</sup>/s)<br /> | D is the diffusion coefficient (cm<sup>2</sup>/s)<br /> | ||
| Line 29: | Line 29: | ||
(After [http://en.wikipedia.org/wiki/Mass_diffusivity#Temperature_dependence_of_the_diffusion_coefficient Wikipedia])]] | (After [http://en.wikipedia.org/wiki/Mass_diffusivity#Temperature_dependence_of_the_diffusion_coefficient Wikipedia])]] | ||
**C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds. | **C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds. | ||
| + | |||
| + | *'''Enzyme concentration''' | ||
| + | **MATLAB - | ||
| + | **Kappa - | ||
| + | **C - | ||
=== Computational cost === | === Computational cost === | ||
Revision as of 17:11, 11 September 2011
Model Comparison
Contents |
The approaches
- MATLAB - Within the reactor tasked with degrading cellulose into glucose in the biorefinery, temperature, enzyme concentration, substrate reactivity as well as xylose, cellobiose and glucose inhibition all govern the amount of glucose product. Deterministic modelling using a set of ordinary differential equations highlights the essential kinetic relationship among the enzymes, exo/endo-glucanase and β-glucosidase. By solving these governing equations using the numerical tool MATLAB the level of degradation is qualitatively predicted.
- Kappa - As an alternative, stochastic models were created using the Kappa language. The system is defined in terms of many discrete agents and rules of their interaction. The Kappa simulator then uses probabilistic equations to simulate the evolution of the system, incorporating an indeterministic element into the system.
- Spatial kappa - Because of problems with the Kappa lang\uage, we decided to use a spatial extension developed by the Edinburgh 2010 iGEM team. This adds extra functionality to the language by introducing the concept of space.
- C model - Intended more as a demonstration of synergy than an accurate model of the world, the cellulose is represented using a simple two-dimensional grid, on which enzymes move using Brownian motion. This is an ad hoc model made in a general programming language. It was inspired by cellular-automata systems, though cannot really be considered one.
Flexibility
We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme.
- Temperature
- MATLAB - Very flexible as it incorporates the Arrhenius law which models the temperature-dependent reaction rate constant.
- Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:
- C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds.
- Enzyme concentration
- MATLAB -
- Kappa -
- C -
Computational cost
The MATLAB and C models do their work in relatively short periods of time. By contrast, the Spatial Kappa model takes a significant length of time.
Representing reality
The MATLAB model is based on the empirical literature, and so should be the best representation of reality.
However, since literature was not available for the synergistic system (with closely linked enzymes) we are considering, we had nothing to base a MATLAB model of synergy on. So, our only MATLAB model is the non-synergistic system.
The C and Spatial Kappa models were capable of comparing a synergistic and a non-synergistic system, but in both cases the model is highly abstract. The C model uses a two dimensional grid, while the Spatial Kappa model uses 9 compartments, with molecules travelling between them.
Ability to reach steady state
We found that the equations used in MATLAB for deterministic modelling only gave sensible answers when the model parameters remained within certain limits. Outside those limits, results could be physically impossible; e.g. producing negative amounts of cellobiose and so breaking the law of conservation of mass. The deterministic model always had reactants available, i.e. cellulose able for every reaction, ensuing it would never reach zero. A 'stress test' was carried out simulating the model over one hundred thousand hours confirming this. Therefore, within the limits of differential equation based modelling, it is unlikely to reach a mathematical steady state. An engineer considers the system to be in steady state when 99% of the initial amount of cellulose has been degraded, which was found to occur after 8000 hours. However, the 'stress test' revealed (Figure 3) that neither the mathematical nor engineering concept of steady state will be reached for cellobiose and glucose in the MATLAB model.
By contrast, in the C model and Kappa model, cellulose, glucose and cellobiose all reach steady state within a finite period of time. Analysing steady state is important to find out whether a system accumulates excess mass or energy over the time period of interest. Looking at the MATLAB model one asks, is the system inherently thermodynamically unstable or is there a flaw with the model?
 "
"