Team:Sevilla/Modelling
From 2011.igem.org

Wire Kinetics
Our approach to the modeling of our project is centered in the properties of wires. A wire is composed by three elements: EHW, the Emitter Half-Wire, a cell with the ability to produce an arbitrary BioBit "i" at an spacefic rate; the SINK, a cell that can degrade the BioBit "i" at another specefic rate and a RHW, the Receptor Half-Wire, that's able to sense the concentration of "i" in the culture media and induce gene expresion in response to it. Our project is based in CBW, Chemical-Based Wires, so the BioBit is a chemical compound, in our case, an quorum sensing AHL molecule, it doesn't matter which one (we also consider the LBW, Light-Based Wires, where a light with a specific spectrum is the BioBit). We are going to assume that the RHW and concentration of "i", [i], is known. We don't want to know the association constant of the molecule to its receptor, but the relation between the concentration of i and the induction of a reporter gene. It would be perfect if we could know the concentration of a BioBit i inferred from the properties of the EHW and the SINK, the two types of cells, in our case bacteria, that are going to define the final concentration of the BioBit "i".

First consideration we have to know is if our circuit is going to run in the exponential phase of growth, or in the stationary phase. We are going to assume that it is going to work in the stationary phase, where the bacterial densities are constants. So, let next equation be the rate of BioBit "i" production and degradation:
Where K_B is the rate of biosynthesis of BioBit "i" by the EHW and ρ_E is the density of EHW bacteria in the culture, and K_D is the rate of degradation of BioBit "i" by the SINK and ρ_S is the density of SINK bacteria in the culture. Now, you can see the sequence of calculus until get the primitive:
Now, we assume that the concentration of i(t) at t=0 is i(0) to find the value of the constant:
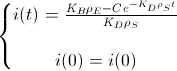
And this is the BioBit i concentration function of time and taking into account the density of bacteria and the rates of production and degradation of "i":
Now, it is interesting if we can get the concentration of BioBit "i" at equilibrium, this is, when time tends to infinity:
Another interesting thing that we can obtain from that equation is the time it takes to reach a certain fraction α (from 0 to 1) of equilibrium concentration:

So, we have a very interesting equation with great potential but, how can we get the values of biosynthesis and degradation constants and the bacterial densities? The first thing we have to do is to create a cell with a RHW(i) coupled to a reporter gene (lacZ with ONPG, for instance), that is RHW_i>lacZ, and then, we make a messure of reporter activity for some differents concentrations of BioBit "i" over time:


Now, we have to build another construction to get the behaviour of the EHW, a RHW(j) coupled to the EHW(i):

Next experiment will let us to characterize the EHW biosynthesis constant. Once you have another verified RWH, RHW(j) in this case, you have to add the enought amount of "j" bbit to the medium for highest gene expresion, then, measure the reporter signal over time and find the curve that fits with it using the curve for RHW(i). This will let us know, if we consider the first part of our initial equation, kinetics constants of our EHW:
Considering the initial conditions,
The solution of the equation is:
So, with the previous experiment, we can get pairs of data like {t,i(t)} taken from the selected curves. And, if we know the bacterial density of EHW(i) (it would be necessary to find the relation between cells/mL and DO(&lamda;=600) to facilitate work), we can estimate K_B.
To estimate the SINK kinetics, we have to build a bacteria with the SINK(i) set of genes and the bacteria with the RHW(i)>ReporterGene configuration taken from the previous experiments. We need culture media with some differents known concentrations of bbit "i" and SINK bacteria. Then, we have to let pass a fixed amount of time and filter the culture media. And now, we have to add RHW(i)>ReporterGene to the filtered media and check the generated curve from the characterization experiment of RHW. This will generate pairs of data like {i(0),i(t)} with "t" a fixed constant. Finally, we have to consider the kinetics of isolated sink:
And the conditions are:
So the final equation is:
And from here, we can get an estimation of K_D using the pairs of {i(0),i(t)} data. This equation is not only useful to characterize the SINK degradation constant. When a wire is switched off, the amount of bbits in media is fixed because its productions stops. Usually, it will be the equilibrium concentration of bbits. We can get the time that takes to reduce this concentration to a fraction α of initial amount (α is between 0 and 1); this is what we call the extinction time:
To conclude, we consider you have to see is the graph of i(t) function of time and b=K_D*ρ_S, once fixed the K_B*ρ_E value (in this case is equal to 1):

The units of time are minutes and liquids are messured in mL. The units of other constants are:
I'm pretty sure this little dissertation could be extended a lot, but the main concepts has been exposed here, and they are enought to addapt and use in your wire characterizations. You can write me to biotoscano@gmail.com to discuss the wire kinetics.
Thanks, Carlos Toscano Ochoa (biology student and amateur mathematician)
(this is me, conceiving all this disturbing math models)
 "
"


