Introduction
Once we sketched out schematic graphical models of vitamin A and vitamin C production, we set out to find the perfect modeling software. We wanted something simple, expressive, powerful, and extendable. We started where last year's modeling prize winner left off: Kappa.
Objectives
- Compare the various modeling languages and platforms available
- Use our choice modeling language to develop a generalizable BioBrick model
A BioBrick in Kappa
BioBricks are meant to be reusable and composable. While the BioBrick sequences may follow these principles, models of BioBrick-based systems often do not. Ty Thomson's Kappa model is a good example of an attempt to standardize BioBrick model[1]. Thomson's model is designed for use in E. coli, which alone limits its power and would force us to redesign it in our application. However the model suffers from more severe and general drawbacks. In order to take advantage of Kappa's rule-based engine, Thomson creates a general DNA agent with upstream, downstream, and binding sites. Thus any rules applied to DNA will apply to all BioBricks. However, often you want rules to refer to a specific BioBrick. Different BioBricks make different proteins, will be transcribed at different rates, or bind certain repressors. Thomson gets around this problem with a hack: he creates a dummy binding site called "label" and gives it a state such as "BBa000011" to identify the BioBrick. When, for example, a modeler wishes to specify unique transcription rates for each BioBrick, he or she is forced to write the same reaction for each BioBrick, changing only the rate and the state of the label "binding site". While functional, the unattractive nature of this hack points to a fundamental problem in Kappa.
A BioBrick in LBS
Enter LBS's module facility. Modules allow the modeler to the structure of a complex interaction once, and paramaterize that structure with rates, compartments, and agents. Consider the extremely simple gene expression model below adapted from Pedersen's thesis[2].
module m(comp nuc; rate trnsc; spec gene, prot){
spec mrna = new{};
nuc[gene + rnap ->{transc} gene + rnap + mrna] |
nuc[mrna] ->{1} mrna |
rs + mrna ->{0.1} rs +prot
};
Adding the line m(nucleus, .001, crtI, phytoene_desaturase) will cause gene expression at a specific rate to occur. Unlike in Kappa, this required no "dummy" labeling and no chemical reaction had to be declared. Thus the model's abstract structure is totally separated from the realization of that structure for specific systems. This module can be reused precisely as it is to model another system. Our BioBrick expression model in LBS makes extensive use of LBS's powerful module facility.
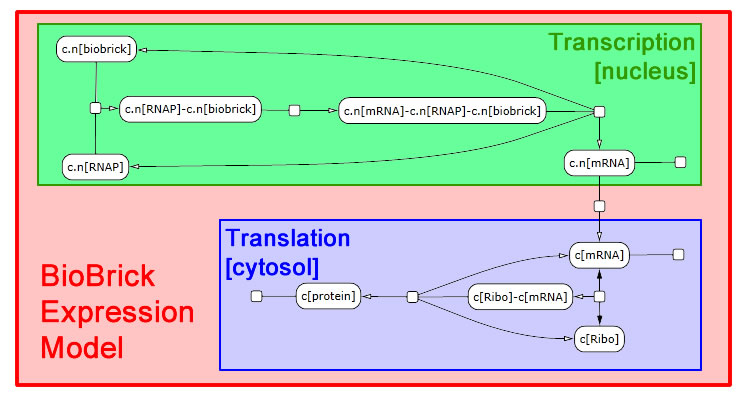
The following schematic depicts the model we developed in LBS. It was generated in part by Visual GEC, the software environment used to compile and run LBS simulations.
Expression module
We interpret gene expression as a process parameterized by a specific gene and by the specific protein to be made. We also require a compartment to serve as the nucleus, since expression in yeast needs to be compartment-aware. While we take the DNA and protein as given, we declare mRNA in the scope of the expression module. Each gene-protein pair will now get a unique mRNA that is abstracted away from all other interactions in the model. We pass off the work to two sub-modules: transcribe and translate. These modules need not themselves be aware of multiple compartments, so we write a line specifying nuclear export of the mRNA. We also perform RNA degradation in the nucleus in parallel with transcription and in the cytosol in parallel with translation.
module express(comp nuc; spec DNA:{bind}, Prot) {
spec mRNA = new{up:binding,down:binding};
nuc[ transcribe(DNA:{bind}, mRNA:{down}) | mRNA ->{rna_deg} ] |
nuc[ mRNA ] ->{export} mRNA |
translate(mRNA:{up}, Prot) | mRNA -> {rna_deg}
};
Transcription module
Transcription requires a DNA segment and an mRNA product. In our model, RNA polymerase, which was declared globally, binds DNA. Then the mRNA molecule appears also bound to RNA polymerase. Finally, the three molecules dissociate. These reactions are irreversible.
module transcribe(spec DNA:{bind}, mRNA:{down}) {
RNAP{dna} + DNA{bind} ->{rnap_bind} RNAP{dna!1}-DNA{bind!1} |
RNAP{dna!1}-DNA{bind!1} ->{transcription} mRNA{down!2}-
RNAP{dna!1,mrna!2}-DNA{bind!1} |
mRNA{down!2}-RNAP{dna!1,mrna!2}-DNA{bind!1} ->{termination}
mRNA{down} + RNAP{dna,mrna} +
DNA{bind}
};
Translation module
The translation module is similar to and even simpler than transcription. mRNA binds a ribosome (declared globally) in a reversible fashion. Once bound, the ribosome can generate a protein and release both the protein and mRNA in a single step.
module translate(spec mRNA:{up}, Prot) {
Ribo{mrna} + mRNA{up} <->{ribo_bind}{ribo_unbind}
Ribo{mrna!1}-mRNA{up!1} |
Ribo{mrna!1}-mRNA{up!1} ->{translation} Ribo{mrna} + mRNA{up} + Prot
};
Parameters for this model can be found here.
A Simplified Expression Model
The expression model above requires the number of ribosomes and polymerases available to our system, and the various rate constants associated with them, to be estimated. We can measure the final quantity of protein produced and the number of copies of the gene introduced into the cell, but this information is insufficient to estimate all the parameters in the model. Further, literature values regarding these values are sparse, crude, and often contradictory. We decided to build a simplified model with fewer parameters.
This system is so simplistic that it is quite easy to solve for the steady-state concentrations of all species analytically. In fact, we find that if ts = transcription rate tl = translation rate p = protein degradation rate r = mRNA degradation rate c = number of gene copies in the cell
\[[Protein]=(t_{s}\cdot t_{l})/(p\cdot r)\cdot c\]
This is useful when translating our pathway optimization results into an implementation strategy for real organisms. We perform our optimization on Matlab models that do not include gene expression. Thus the optimal parameters are stated in terms of enzyme concentrations. Given the target enzyme concentrations suggested by our optimization algorithm, an accurate enough expression model could then allow us to infer optimal gene copy numbers and promoter strengths. We can then search a database of yeast promoter strengths to select the promoter that should be used and the gene copy number needed. In practice this is unrealistic. Predictive models of mRNA lifetime do not exist. Transcription and translation rates are fairly sensitive to the specific codons used. These processes are also exceptionally noisy. It turns out that the metabolic kinetics are much easier to describe accurately, so our results from optimization are useful. However, inferring the genetic construct needed to achieve the optimal protein concentrations will require trial-and-error at the bench.
References
[1]Ty Thompson. Rule-Based Modeling of BioBrick Parts. http://www.rulebase.org/books/184351-Rule-Based-Modeling-of-BioBrick-Parts.
[2] Pedersen, M., & Plotkin, G. D. (2010). A language for biochemical systems: Design and formal specification. (C. Priami, R. Breitling, D. Gilbert, M. Heiner, & A. M. Uhrmacher, Eds.)Transactions on Computational Systems Biology XII, 5945, 77-145. Springer Berlin Heidelberg.
 "
"