From membrane tension to liquid flux

To deduce the force exercising on the tube from membranian pressure, please refer to an explanation figure below :


Fig1: Tension-force_explanation / The force applied to the nanotube as a function of the surface tension force.	Fig2: Geometry / The system geometry. state during the steady state phase.

Here T is a surface tension, N is a resulting force of the area of the tube attachment to the bacterium, Δα or α is the half of the angle with a vertex in the center of the bacterium and between the tube extremities. Only this zone is giving a non-compensated contribution to the resulting force.

So the force exercising on the tube is given by the formula :

where r is the tube radius, R is the bacterium radius. At first approximation we can consider the process a serie of quasi equilibrium states, that it is rather slow that acceleration of the membrane is zero. We find the speed of the tube membrane at every moment of time out of the second Newton's law :

where ΔF is the difference of the forces applied to the extremities of the tube. The number of phospholipids in two bacteria will change according to these equations :

where N1, N2 are numbers of phospholipids on the membrane of the first and the second bacterium corrispondingly, ΔS is the surface per one phospholipid one the tube. Cutting the whole period of time of our process into laps of time dt we should solve the Poiseuille equation each time reevoluating the difference of pressure :

The Poiseuille equation :

where L is the total length of the nanotube, r is the distance from the center line of the nanotube, R is the radius of the nanotube. The volume flow of the liquid passed through the nanotube is :

By integrating the last formula in time we will get the mass of the liquid passed from one bacterium to another :

where T is the time of the process.

Getting good parameters

We have done several simulations where the system consisted of two spherical bacteria of radius R1 and R2, the nanotube of the length L and the radius r between them, and the number of phospholipids N1 and N2 on them. The nanotube dimentions we have taken from the article published by Dubey and Ben-Yehuda [1] (r = 100 nm, L = 1 µm). The ideas about what values to take for R1, R2 and N1, N2 we got from the bionumber's site <a href="https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion#references"> [2]</a>. We have checked several sets of parameters :

N1 = 2*10⁶, N2 = 1*10⁶, R1 = R2 = 0.5 µm;

N1 = 1*10⁷, N2 = 5*10⁶, R1 = 2 µm, R2 = 1 µm;

The value of dynamic viscosity of phospholipid bilayer taken is 10 Pa.s, a bit more than what can be found for castor oil.

Analysing the results and conclusion

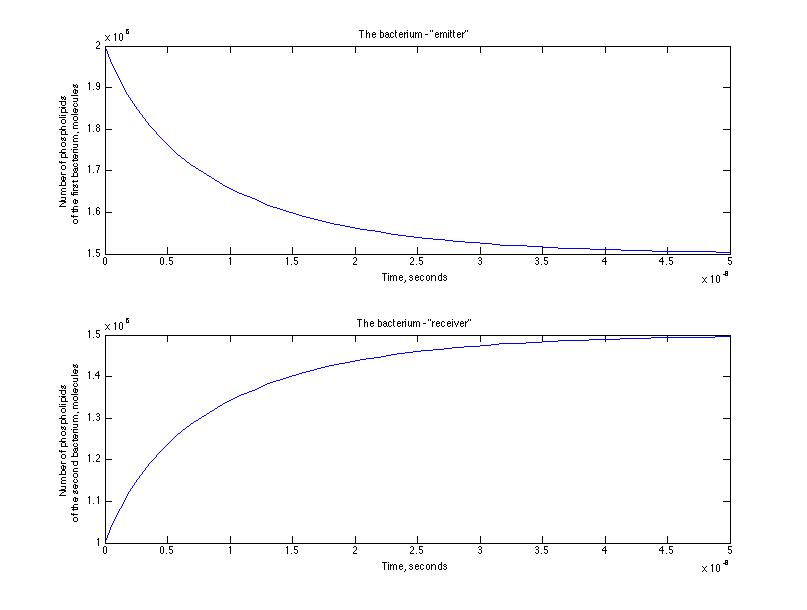
Here is the representation of the cinetic between the emitter and receiver - the number of phospholipids passed from the emitter to the receiver through the nanotube.

Number of phospholipids in each bacteria

After a set of simulations we have estimated the characteristic time of the process and it was of the order of 10^-8 seconds for the first simulation and 10 ^-6 seconds for the second one. That means that we were right at the beginning that an assisted diffusion process is much faster that a passive diffusion.

The masses transported are of the order of 10 ^-18 kg, which is an interesting result. In terms of the volume exchange : we can observe that about 10 ^-21 m ³ of liquid is transfert from the emitter to the receiver. 0,1 % of the emitter volume is transported due to an assisted diffusion. This doesn't seem much and it certainly doesn't entirely explain the original gfp diffusion experiment. It is nevertheless interesting to see such orders of magnitude.

Anyway this process can assist the passive diffusion in a way that if we have a lot of molecules in one bacterium that are localized near the membrane and nanotubes, it may accelerate the diffusion.

We still have to work on this model in order to tinker with some of the problem parameters. This might permit us to see a faster and more significant molecule transport through the nanotubes.

References

Intercellular Nanotubes Mediate Bacterial Communication, Dubey and Ben-Yehuda, Cell, 2011, available <a href="http://bms.ucsf.edu/sites/ucsf-bms.ixm.ca/files/marjordan_06022011.pdf">here</a>
BioNumbers <a href="http://bionumbers.hms.harvard.edu/">here</a>

</html>

Team:Paris Bettencourt/Modeling/Assisted diffusion/From membrane tension to liquid flux

From 2011.igem.org

From membrane tension to liquid flux

Getting good parameters

Analysing the results and conclusion