Team:Edinburgh/Cellulases (MATLAB model)
From 2011.igem.org
Cellulases (MATLAB model)
The most important part of the biorefinery is the reactor where cellulose is converted to glucose. But accurately predicting how much is converted, using synergy between enzymes is difficult without literature to provide the ordinary differential equations (ODE's) and the kinetic parameters. Therefore this model only looks at the free floating enzyme approach (non-synergy). It is deterministic i.e non random and is set by a series of initial conditions.
Contents[hide] |
Assumptions
The mathematical model is based on the ODE's and kinetic parameters outlined in [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Kadam et al, 2004]. The following are its assumptions and basis:
- Rate equations assume enzyme adsorption follows the Langmuir isotherm model
- Glucose and cellobiose which are the products of cellulose hydrolysis, were assumed to, 'competitively inhibit enzyme hyrolysis' [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Kadam et al, 2004]
- Assume all reactions follow the same temperature dependency Arrhenius relationship. However it should be different for every enzyme component, 'because of their varying degrees of thermostability, with beta-glucocidase being the most thermostable. Hence the assumption is a simplification of reality' [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Kadam et al, 2004]
- Conversion of cellobiose to glucose follows the Michaelis-Menten enzyme kinetic model
Equations
Rate Equations
Constants
knr - reaction rate constant for reaction n
EnB is the bound concentration for exo and endo-beta-1,4-glucanase for reaction n
Rs - substrate reactivity parameter
S - substrate reactivity at a given time (g/kg)
G2 - concentration of cellobiose
G - concentration of Glucose
X - xylose concentration
KnIG2 - inhibition constant for cellobiose at reaction n
K1IG - inhibition constant for Glucose at reaction n
K1IX - xylose inhibition constant for reaction n
Note: Assuming no xylose inhibition therefore X=0
Langmuir Isotherm

Constants
exo and endo-beta-1,4-glucanase, i=1
beta-glucosidase, i=2
Eimax - Maximum mass of exo and endo-beta-1,4-glucanase (i=1) or beta-glucosidase (i=2) that can be absorbed onto a unit of mass substrate
Kiad - Dissociation constant for enzyme i
EiF - Free enzyme concentration for enzyme i
S - Substrate reactivity at a given time (g/kg)
Mass Balances
Arrhenius Equation
Constants
Kir - Reaction rate constant of reaction i
Eai - Activation energy of reaction i
R - Universal gas constant
Construction of Model
The model was constructed using the numerical programme [http://www.mathworks.co.uk/products/matlab/index.html MATLAB]. A script file was generated which holds the variable dictionary, constants, temperature dependency equations, ODE45 and plot command.
A separate function file to the script is created as script files can only operate on the variables that are coded into their m-files. Rs, the substrate reactivity parameter changes at every iteration because it is dependent on the S the substrate concentration at a given time, the substrate being cellulose. Therefore S at the first iteration is So, the initial substrate concentration. At the second iteration S is the previous value calculated by the ODE, and so on. After each step the new value of S, is fed into the function file and is used for calculating the reaction rate constant for cellobiose and glucose etc.
ODE45 calls on the function file to calculate the rate equations and then substitute them into the respective mass balance. A numerical integration is performed and the results can be seen below. ODE 45 is used as it is more accurate than other solvers [http://www.mathworks.co.uk/help/techdoc/ref/ode23.html (Mathworks)]. It is based on an explicit Runge-Kutta formula and is a one step solver.
Results
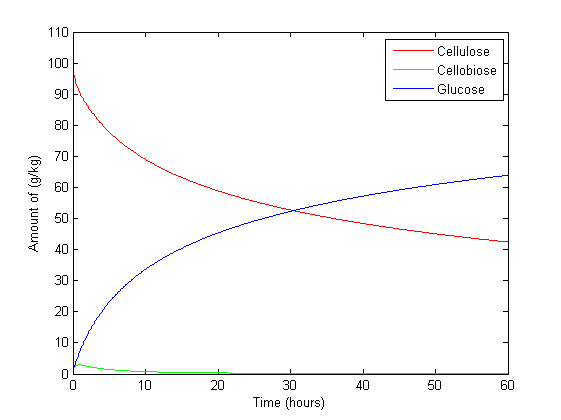
Figure 1 is set with β-glucosidase at its maximum concentration and Figure 2 with Exo/endo-glucanase at maximum. This is to compare the effect of certain enzymes on cellulose degradation and glucose production. The result is consistent with what is expected. Exoglucanase chews away at the end of a cellulose chain, producing cellobiose sugars and endoglucanase cuts cellulose chanins in the centre, turning one chain into two. This concurs with the results, with Figure 2 modelling markedly higher amount of cellulose at the maximum amount of exo/endo-glucanase than that of Figure 1. Whereas β-glucosidase cuts cellobiose in half, producing two glucose molecules. Figure 1 which β-glucosidase is at its maximum produces 167% more glucose than in Figure 2 with β-glucosidase at its minimum at steady state.
Cellobiose in Figure 1 increases to 10 g/kg in 20 hours but after 50 hours begins to decrease. This is because β-glucosidase starts to convert it to glucose. This result cannot be seen in Figure 2 with little β-glucosidase present in the system as a result cellobiose increases to 60 g/kg.
Figure 3 is under the same conditions as Figure 1, but its x-axis is set to a semilog scale to exasperate what happens over a longer period of time. The effect of high β-glucosidase can better be seen with the complete conversion of cellobiose to glucose. However interestingly the effect of glucose over time highlights one of the limitations of an ODE based model. The amount of glucose increases beyond the amount of cellulose present initially, which breaks the law of conservation of mass. This is the cause of continuous iterations by MATLAB which doesn't stop after a certain point in time. The ODE therefore has limits within itself were it works best. Which is why Edinburgh decided to construct a stochastic based model,Kappa. Rules are defined which describe how the model moves from one state to the next. Therefore this problem is avoidable.
Download MATLAB file
You can download the ready model as a .zip file:

References
- Kadam KL, Rydholm EC, McMillan JD (2004) [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Development and Validation of a Kinetic Model for Enzymatic Saccharification of Lignocellulosic Biomass]. Biotechnology Progress 20(3): 698–705 (doi: 10.1021/bp034316x).
 "
"