Team:Harvard/Project/Bioinformatics
From 2011.igem.org
Overview | Bioinformatics | Chip-Based Library | Plasmid Construction | Selection Strain Engineering | Protocols
We emailed the OPEN consortium and Anton Persikov to acquire their respective databases of zinc fingers: Persikov had complied the results of the past 10 years of zinc finger research. We then decided how to analyze this data and choose targets for new zinc fingers (details below). Then we programmed our ideas into a Python program, and generated 55,000 potential zinc fingers.
Contents |
Terminology
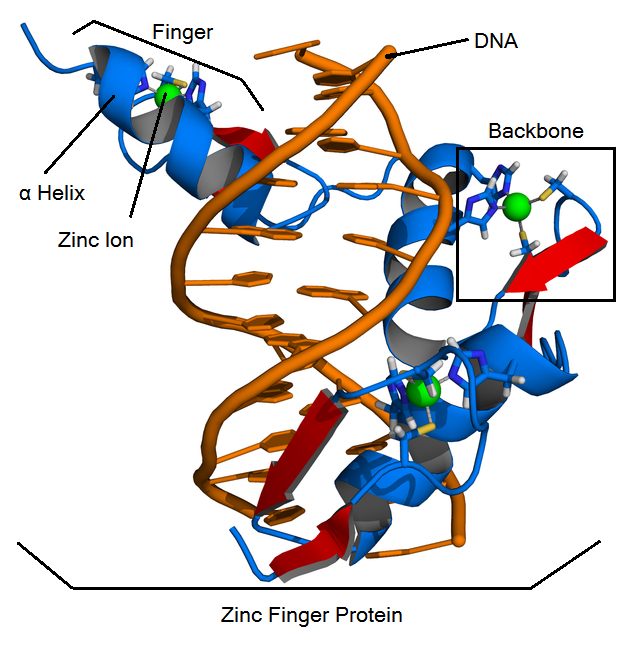
- Backbone: contains most of the amino acids of a zinc finger protein: zif268 is the most famous backbone.
- Fingers: contain a backbone and a helix, bind to a 3-base DNA triplet
- Helix: the alpha helix in a finger. It is responsible for binding to a DNA triplet. Helices are made up of 7 amino acids, and fit into a specified position in a backbone. Amino acid positions are specified by -1,1,2,3,4,5, and 6.
- Zinc finger proteins (ZFPs): arrays of three fingers that bind to 9 bases (3 triplets) of DNA.
Past Zinc Finger Designers
Designing new zinc finger proteins (ZFPs, which are arrays of three fingers) is not an easy task: how they bind and interact with DNA bases is not fully understood, and is an active area of research ([http://www.princeton.edu/~persikov/publications.html Persikov]). Notable past attempts to create novel ZFPs ([http://www.nature.com/nmeth/journal/v8/n1/full/nmeth0111-53.html CODA], [http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2535758/ OPEN]) tried a two distinct methods: CODA took a modular approachOPEN took two known fingers from an array, and randomized protein sequences to try to generate a third finger to bind a new triplet:
Both techniques were successful in finding ZFPs to bind to novel DNA sequences [how successful?]
Our Approach
Improving on the concept of OPEN, we decided to design ZFPs where the first two DNA triplets can be bound, but the third cannot. For example, if the sequence GTG GGA CCA can be bound but GTG GGA TGG cannot, we would use the first two fingers and generate the third. OPEN simply randomized amino acid sequences to try to create a third finger: we wrote software that uses data from known fingers to "intelligently" generate new fingers.
Choosing Target Sequences
Someone who is not me will write this section.
Data and Analysis
OPEN provided us with a spreadsheet of ZFPs produced by their research. Anton Persikov, during his own ZFP research, has compiled a database of ZFPs from studies from 1980-2005 which he shared with us.
From these two datasets, we distilled over [3000] unique ZFPs which contained approximately [1000] unique fingers.
We analyzed this dataset for frequency (how often a given amino acid appears in a given position in the helix) and pairing (if amino acid A is in position 1, how often is amino acid B next to it).
Helix Dependencies
Amino acids do not exist in a vacuum: they must somehow be affected by amino acids around them. Besides pairing data, we realized that other interactions could be taking place, and that we needed a way to see these other relationships.
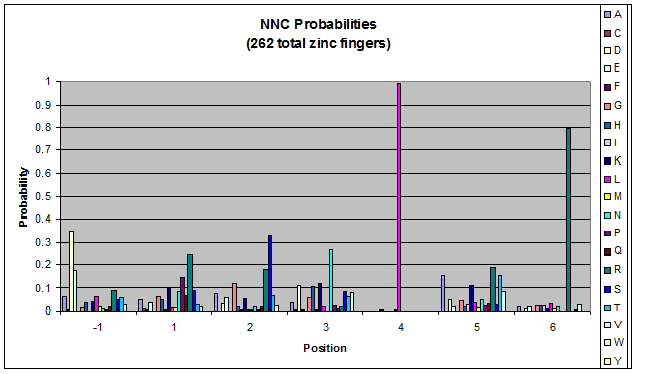
We know that the DNA bases affect the amino acid sequence, so we started looking for evidence that, for example, changing the third base (going from NNA to NNC, etc) affects position -1.
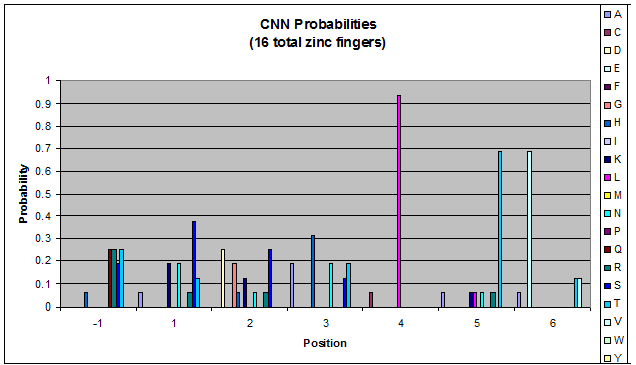
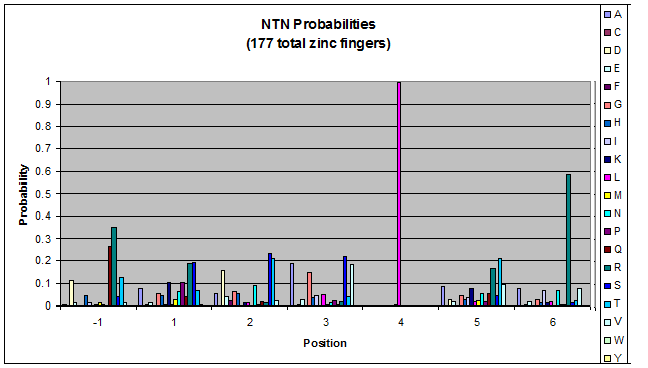
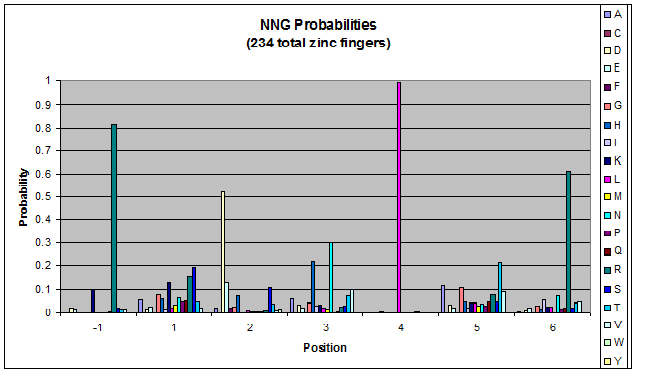
To do this, we created these graphs of the frequency of amino acids in each position, and then [http://en.wikipedia.org/wiki/Blink_comparator blinked] the graphs against each other to see what changes. We looked at the probability graphs to determine which amino acid positions on the finger's helix interact with which bases. For example, if you compare NAN to NCN, you will see a large change in the asparagine content in position 3.
We saw some interactions that are fairly well estabilished [Persikov], while others have been more recently proposed [Persikov].
Click on the triplets on the left to compare the frequencies for various DNA triplets:
| GNN |
| TNN |
| CNN |
| ANN |
| NGN |
| NTN |
| NCN |
| NAN |
| NNG |
| NNT |
| NNC |
| NNA |
(A more rigorous way to calculate this is to calculate the entropy change as you change the amino acids in each position. But that is computationally intensive)
By doing this, we were able to see several patterns.
- xNN(Vary base 1): Amino acid 6 changes
- NxN(Vary base 2): Amino acid 3 changes
- NNx(Vary base 3): Amino acid -1 and 2(?) changes
Our program looks at dependencies between amino acids when generating sequences.
We decided on these amino acid dependencies, using both established data and patterns we saw in the OPEN data:
- -1 and 2
- 2 and 1
- 6 and 5
Because there is not much data for 'CNN' and 'ANN' sequences (with 16 and 29 known fingers that bind to each triplet, respectively), we should use pseudocounts for these sequences, so that our frequency generator is not too biased toward probabilities that may not be significant.
Programming
Overall Method: Probabilities and Randomization
Our generation program uses these amino acid frequencies as probabilities that position X contains amino acid X, given what triplet we are trying to bind. Using the dependencies we found, we change which frequency tables are used to generate the new helix. Frequency tables are built using the data from the above graphs.
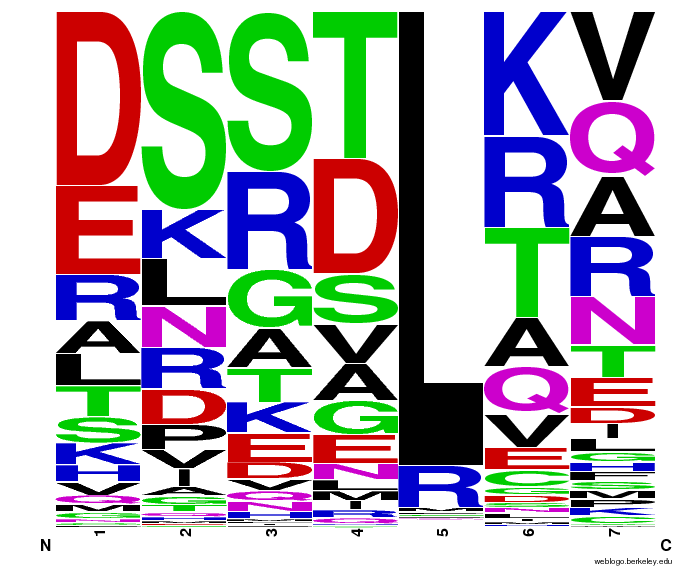
See the image at right for explanation on how we turn probabilities into amino acids.
To generate one helix (7 amino acids), the program goes through the following steps:
| Step | Example for TGG |
| Generate an amino acid for position -1 (P0), using probabilities only from NNx | R _ _ _ _ _ _ |
| Taking into account the amino acid chosen for P0, generate P2, also using probabilities only from NNx | R _ S _ _ _ _ |
| Taking into account the amino acid chosen for P2, generate P1, using overall probabilities for P1 | R L S _ _ _ _ |
| Generate P3, using probabilities only from NxN | R L S H _ _ _ |
| Generate P4, using overall probabilities for P4 | R L S H L _ _ |
| Generate P6, using probabilities only from xNN | R L S H L _ M |
| Taking into account the amino acid chosen for P6, generate P5, using overall probabilities for P5 | R L S H L Q M |
These steps are based on the relationships we found from reading papers [Persikov] and studying the above frequency graphs, which were created from successful ZFPs.
The generated helix is then placed into a backbone: for example, this helix was placed in the zif268 backbone, giving a finger with a final amino acid sequence of FQCRICMRNFSRLSHLQMHIRTH.
This finger is then reverse-translated into DNA (along with the sequences for the fixed first two fingers of the ZFP) for inclusion in the chip.
Refinement: Pseudocounts
Pseudocounts are necessary for data that has small sample size - we could be missing out on working helices because a letter's frequency is 0 when it shouldn't be. For CNN and ANN, our dataset is tiny compared to GNN and TNN: CNN and ANN have around 20 datapoints while GNN has over 700. Because of this discrepancy in sample size, we must add psuedocounts to CNN and ANN in order to allow for more variation than is shown in our data.
When generating helixes for CTC (because of position 6's reliance on the CNN frequencies) to test psuedocounts, we see in the created sequences the difference pseudocounts make. A psuedocount of .015 changes the frequency of any amino acid from whose frequency is 0 by bumping it up to the value of the psuedocount: ex. A = 0 becomes A = .015, giving A a 1.5% chance of being selected instead of none at all.
Visualizing our data, we get various pseudocount (psu = ) values for position 7 (which, in reality, is position 6 in the helix). The size of the letter directly corresponds to the percentage of sequences that have that letter in that position. A letter that takes up 1/3 of a column is present in that position in 33% of the helices.
Notice how psu = 0 gives only the four letters found in our CNN dataset, while psu > 0 adds in other letters, each with a small probability.
The question is how much psu to add: less means we weight our (possibly flawed) data of proven zinc fingers more. Higher psu adds more randomness (variation) to our sequences, but some (perhaps large) fraction of those sequences will not work, and take away space from the proven amino acids.
We ultimately chose psu = .015 for our software.
Results: 55,000 Possible Zinc Fingers
We made 55,000 sequences, distributed evenly among 6 DNA target triplets. That's 9150 per target.
Because our program's output changes dramatically based on the input triplet, no two sets of sequences are the same:
 "
"