Team:Grenoble/Projet/Modelling/Deterministic
From 2011.igem.org
Modelling - Deterministic
You need MathML supported on your browser to read the equations on this page. However, you can find these equations in the above PDF version.
Our equations and how we obtained them
The Two levels of Modelling
In order to facilitate the construction of the model, we divided the model into two levels :
- Toggle Switch modelling: to predict the state bacteria will be.
- Quorum Sensing and Coloration: to predict where the red line will appear on our device.
The first level of the model will allow us to define the switch conditions in bacteria, depending on the concentrations of pollutant and IPTG. From these results, we could see the switch zone on the device and therefore, the position of the red line. These results indicate how to resize our device to improve the detection.
The second level will provide us with the red line width, an indicator of the system precision. From these results, we could improve the precision of our device, for instance, by choosing between a device with a continuous bacterial layer and a device with strips containing bacteria. Each strip has a different IPTG concentration, but the same concentration of Mercury.
As a proof of concept, we will consider anhydrotetracycline (aTc) instead of Mercury in our model, and the transcriptional regulator TetR in place of MerR. The TetR system is well characterized in E. coli, which facilitates the modelling. In addition, if the system works well with aTc, it should work as well with Mercury, Copper or lead for example.
So in the following chapter, we are going to use TetR instead of MerR and aTc instead of Mercury.
Toggle switch
- Biological Models
- Mathematical Models
A toggle switch consists of two genes, each coding for a protein that represses the expression of the other gene. This double repression system ensures the basic function of a toggle switch: a bistable system which can be switched from one state to the other by putting, in our example, some IPTG or aTc molecules in the medium.
The biological system we are trying to implement is more complex, on both the biological and physical side. However, the toggle switch model is basically the same. In the study of the toggle switch itself, the system can be reduced to a simple two-state subsystem that we will then use for the rest of our modelling. The toggle switch itself is not influenced by the rest of the system, if we do not consider the RsmA regulatory system that will be modeled at the very end of our work. Thus we will be able to model the toggle switch independently and then build the rest of the model upon this basis.
We use a common model for the toggle switch that we demonstrate below. The differential equation describing the production of TetR is as follows
For better understanding of this model we demonstrated it. The differential equation describing the production of xR is as follow :
with [Plac free ] being the concentration of available binding sites - i.e. not repressed by LacI molecule. Plac_free is of course related to the total number of promoters Plac : with [Plac − LacI ] being the concentration of promoters repressed by LacI. If we set we get : We then try to get [LacI] : with [LacI - IPTG] the concentration of LacI bound to IPTG and [LacI - plac ] the concentration of the complex of LacI and the promoter. If we set we get : which finally gives our differential equations for TetR :
The equation can be generalized to account for cooperativity arising from multimerization of the transcription factors, here represented by the cooperativity constant nplac
In a similar way, we obtain a differential equation for LacI:
These two equations can be easily computed with a differential solver. We can precisely estimate the effects of each parameter.Our equations and how we obtained them
Quorum sensing
- Mathematical Models
- With f ([CinI]) being a mathematical function describing the production of QS molecule by CinI enzyme. Basically this fonction would be as follow : But if this reaction is assumed first-order, we obtain :
- With Ddiff being the diffusion coefficient for our Quorum sensing molecule in our medium along spatial dimension x.
- In our case ρvc is a constant (we consider the cells do not grow in our time scale)
- Solvation ot the set of equations (3.1); (3.3); (3.5); (3.6)
-
To solve this set of equations we have to use a matrix that will describe our system in both space and time. for example for the QS molecule outside of the cell :
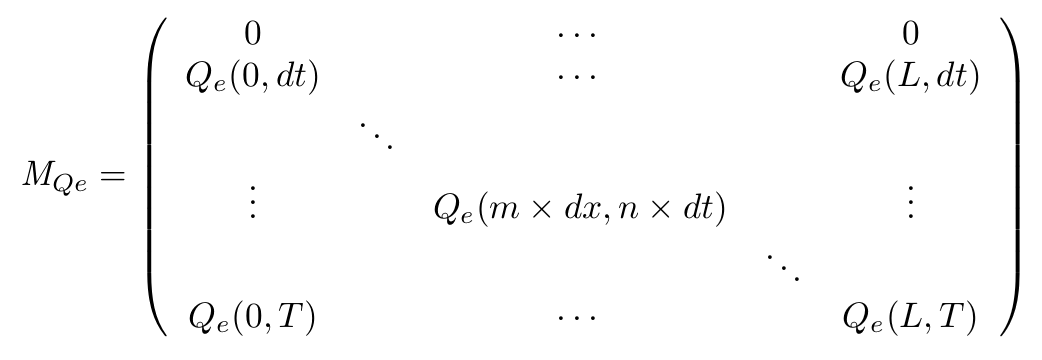
- On the spatial point of view, we only consider the x dimension, as the IPTG gradient will be only evolving along this dimension. Thus we consider the state of our cells is the same along the width of our plate.
- With this Matrix, and after computation of all the terms, we can get the entire behaviour of CinI, CinR, QS inside and outside the cells.
- The first line of the Matrix equals 0. These are the initial conditions we set to 0 at time t = 0s.
- On the borders of the plate (x = 0 and x = L) the model used has to be different, limit conditions will be set.
- Of course, Qi, CinI and CinR matrices will be similarly implemented.
With our continuous equations set, we want to obtain discrete definition of each of the matrices. The interdepen- dancies of the equations imply that the computation of the matrices will be performed on the entire CinI matrix first, then each line of the Qi and Qe matrices will be computed alternatively. Finally CinR matrix computation will be performed.
Parallel computation of all the matrices without proper control is not possible indeed, as the terms of Qi matrix will depend on the Qe terms of the preceding line (and vice-versa). Discretization is obtained with first order taylor series :
with
Our work mainly refers to the models set up by the 2007 iGEM Bangalore team. On the basis of their work we set
up models adapted to our own system. For these reasons we strongly recommend getting familiar with the works
of the 2007 Bangalore team for an easier understanding of the models we used.
The main difference between our models is that their model is designed for a whole medium, in which the concen-
trations of quorum sensing molecules are considered for a whole fixed volume of a medium. Our system, however, is
supposed to describe the spatial diffusion of quorum sensing molecules as well, and therefore needs to be designed
for an infinitesimal volume of medium containing bacteries and outside medium.
A few other differences exist between our model and theirs, mainly due to the fact that the system we intend to
describe is made of other different parts. For example the production rate of our Quorum Sensing enzymes are
directly linked to the previously described toggle switch model.
For these reasons we strongly recommend getting familiar with the works of the 2007 Bangalore team for an easier understanding of the models we used.
Bangalore 07 modeled the behaviour of quorum sensing for a simple quorum sensing system. With the input of the toggle switch model taken into account, we can adapt their equations to our system. With our toggle switch system the production would be ruled by the regulatory network of LacI and TetR :
We can therefore describe the production of CinI and CinRfree inside the cells. Vcomplexation
is the complexation rate of CinRfree with AHL molecule. As a matter of fact CinR will be transformed into
CinR* after being complexed with the Quorum Sensing molecules entering the cell. It is now taken into account via this
complexation rate.
A simple way to write this rate would be as follow :
with Qi being the concentration in QS molecule inside the cell. If we consider that only one QS molecule would
bind to a CinR molecule, we obtain the following equation for CinR :
For the following equations the physical volume considered is an infinitesimal volume of medium along x - i.e. we only consider an l ∗ dx volume of cell, l being the width of our plate and dx an infinitesimal portion of length. In this infinitesimal volume we set a fixed number of non-growing cells and take into account the diffusion from one portion to the next ones.
With the equations set (3.1); (3.3); (3.5); (3.6) we have, we can not use solvers like matlab ODE because of their space and time dependancies. To solve our problem we have to use a space-time derivation matrix we will describe in the next chapter.
With these discrete equations the 4 matrices can be computed through simple calculation loops over each line. The CinI matrix does not depend on space dimension, it is then possible to compute it without discretization with a differential solver.
Our algorithms
In the MATLAB archive that can be found here containing our matlab scripts for deterministic modelling (file Deterministic_archive.tar.gz) you can launch an ODE based simulation (see our ODEs in the two previous sections) with the file biosenseur1Dmain.m.
Several dialog boxes will pop up to enter the specificities of the simulation : (physical specificities of the device, chemical species concentrations and IPTG gradient )
At the end of the simulation you obtain 3 matrices named M_stock, M_QS and M_comp containing the concentrations in each protein species at each time point and on each physical point of the plate. We wrote three MATLAB scripts that display the concentration in proteins dynamically that you can call with DynamicplottingTS, DynamicplottingQS and DynamicplottingCP. For a good understanding of the models and of our results we also wrote a script to illustrate the coloration of our plate through time according to our models named Imageshow.m.
Nullclines and Hysteresis
In order to predict the stability of our system, mathematical studies are necessary.
Nullclines
In a first time, an isocline study is realized.
Nullclines are a classical tool to determine the stationary point(s) of a system. They are obtained by setting to zero the time-derivative of each variable. For instance in our model, d[TetR]/dt=0 allows us to determine the nullcline of [TetR] as a function of [LacI]. d[LacI]/dt=0 allows us to determine the nullcline of [LacI] as a function of [TetR] The intersection point of all the nullclines is a stationary point of the system, when the rate of change of the repressor concentrations are equal to zero.

To facilitate the manipulation of the equations and reduce the number of parameters, we introduce new parameters and concentration variables:
- E_TetR = kplac * [pLac total]
- E_LacI = kpTet * [pTet total]
- [TetR]r = RTetR * [TetR] the relative concentration of TetR
- [LacI]r = RLacI * [LacI] the relative concentration of LacI
After manipulation with these reduced parameters, we get this following equations:

From these equations, we get these figures:

The nullclines are sketched in the figure below. The red line represents the first equation of the system and the green line, the second equation. This figure was obtained with [aTc] = 1E-6 M and [IPTG] = 1,55 E-4 M. These parameters reflect the situation of our device in the center of the plate to a logarithmic gradient of IPTG of 1E-6 M to 1E-2 M
Three stationary points emerge from this graph. These are the three points of intersection of two curves and represent the steady state of the system.
The curves intersect in three different points, meaning that the system has three steady states. One of them is unstable: the middle one. It represents the point where both relative concentrations are equal, which almost never happens in the reality, since the two repressors inhibit each other. Any fluctuation will lead one repressor to take an advantage on the other.

Figure 2:
Nullclines for the left side of the plate
|

Figure 3:
Nullclines for the right side of the plate
|
The left graph represents the left side of the plate: aTc concentration is superior to IPTG concentration and the right graph represents the right side of the plate where IPTG concentration prevails. These figures show that when the concentration of one of the repressors is higher, the system is no longer bistable but monostable.
Points to Remember :
- On the extreme side of the plate, the system is monostable.
- On the switch area of the plate, the system is bistable.
- Bistability, in the switch area, allows us to obtain neighboring bacteria in different states. These bacteria can communicate together(see the Design and Principle section) and stimulate the coloration.
Hysteresis
The goal of the hysteresis study is to established the switch conditions when the toggle switch is already blocked in a predefined way. In our mathematical studies, we blocked the system in the lacI way with different preliminary aTc concentrations. To get hysteresis curves, after blocking the system, we grow the amount of IPTG to see from which concentration the system will switch. Then, we decrease IPTG concentration to see if the system switch back to the initial state at the same IPTG concentration. The blue curve shows the evolution of TetR concentration when IPTG concentration grows. The red curve shows the evolution of TetR concentration when IPTG concentration decreases.

Important values to exploit from these curves are the two switch concentration of IPTG. On this curve, we can get the switch up concentration: ~ 1E-2 M of IPTG and the switch back concentration ~ 3E-5 M.
The switch back concentration is very similar to the dissociation constant between lacI and IPTG (which is 2.96E-5 M). It means that, when there is not enough IPTG in the bacteria, the IPTG-lacI complexe is faster degraded than produced. So the repression is no longer effective.
The following curves show different hysteresis for growing aTc concentrations.
The two first curves (for aTc = 1E-9 M and aTc = 1E-8 M) show that the switch up and switch back concentrations are the same. This concentration is ~ 3E-5 M, the dissociation constant between lacI and IPTG. The last curve (for aTc = 1E-7 M) shows that the switch back concentration stay the same. But the switch up concentration is higher. In fact, for aTc concentration superior to 1E-7 M, the switch up concentration is growing with aTc concentration.
The concentration of aTc 1E-7 M appears to be the limit of sensibility to the toggle switch. This concentration represents the dissociation constant of aTc to TetR repressor.
Points to Remember :
From this mathematical study, we can get the limit of detection of our system: which is close to the dissociation constant of aTc and is repressor.
 "
"


