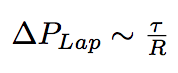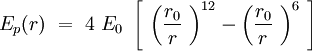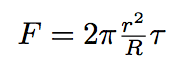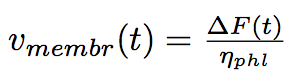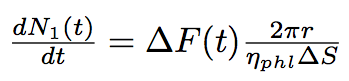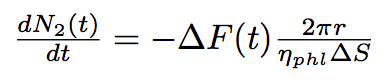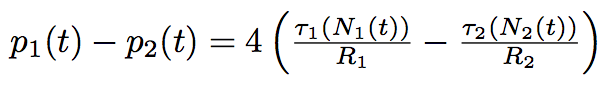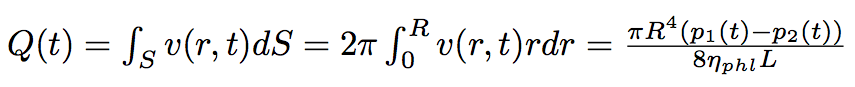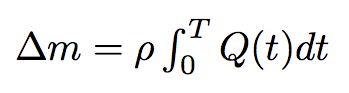• Home
• Presentation
  • Overview
  • Potential applications
  • Collaborations
  • The team
  • Acknowledgements →
    • Host laboratory
    • Sponsors
• Designs
  • Designs overview & concepts
  • Designs list
• Modeling
  • General overview
  • Modeling results for our designs →
    • The basics
    • Our assumptions
    • T7 polymerase diffusion
    • tRNA diffusion
    • ComK/ComS system
    • Parameters
  • Results of our passive diffusion model
  • Toward assisted diffusion
• Data
• Results
  • Achievements
  • Methodologies →
    • Microscopy
    • Micro-fluidic
    • Integration in B.subtilis
    • Kinetics
  • Parts list
  • Notebook
• Human practice & Safety
  • Human practice
  • Safety
  • Brainstorming
  • Bonus track

Assisted diffusion

Introduction to the model

The diffusion through the nanotubes is a fast process. In the previous page, we tried to explain the speed observed with the brownian motion of the cell comonent. But the article from Dubey and Ben-Yehuda suggests that the diffusion is an active process. Several points can be opposed to this statement: First, the diffusion is happening with molecule of different natures which have nothing to do with the natural compoments of a cell (no specificity in the transport) Unlike the mamalian cells, the tube seems to have no "railroad" but the membrane itself design for such a transport The question is: Can we imagine a process that is faster than passive diffusion but does not rely on specific interractions?

The answer is probably yes, and in this page we propose a new model, really challenging for the mind, but that can possibly explain the speed of the diffusion process through the nanotubes.

General physical concepts and hypothesis

How a connection between two bacteria might be established

For different reasons the inner pressure of a bacterium can grow locally. That can cause the tube growth (if the pressure is big enough). If two bacteria are close to each other, their tubes could meet and even touch each other on the extremities. In this situation the phospholipids on the ends of the tubes are rather instable. Their hydrophobic part is more exposed to water because of the high curvature on the extremities. So the energy-preferable state is to fuse. In this case there is no specific protein involved to do the fusion, so it seems to be the explanation of the process closest to reality.

In further paragraphes we will be more interested in what happens after the membrane fusion.

Starting with a physical analogy

Imagine two bottles of gaz connected by a tube. The first one have a higher pressure than the second one. In the first one, there are a few molecules of another nature diluted in the gaz. We follow these molecules.

When you open the tape, the bottle with a higher pressure will equilibrate with the other one my moving a certain quantity of its particles through the tube in the direction of the second bottle. These moving molecules will drag with them the components diluted in the gaz and a few of these molecules will be transported to the other bottle.

From the analogy to the biology

Of course the cell is not a bag of liquid under pressure. The water is equilibrated at both sides of the exterior membrane. The pressure, we are dealing with, is not related to water or osmotic pressure (that is a "passive diffusion thermodynamical pressure"). There is a part of the cell we are not used to think about that undergo a certain variablilty of pressure: the phospholipid membrane!

Let's evaluate the constraints that impact the membrane. As it is a Gramm positive bacteria, the external sugar envelope impose the shape of the bacteria. On the other hand, the osmotic pressure is pushing the membrane against the sugar wall. At every moment inside the membrane the number of phospholipids is fixed, but this number can fluctuate depending on the phospholipid production. So we can pretend that our system is evoluating through a serie quasiequilibrium states.

Fig2: If there is an excess of phospholipids, the membrane is under compression	Fig3: If there are not enough phospholipids, the membrane is under extension

When the cell "start the communication", a flow of phospholipids of the membrane can pass from the cell that have the highest membrane tension to the other one. To pass from one cell to another, phospholipids run around the tube.

The newly arrived phospholipids change the membrane tension of the bacterium and, under our hypothesis of constant volume, which is justified by the sugar layer that "forbids" the bacterium to grow. As a consequence they change the internal Laplacian pressure of the bacterium.

where R is the radius of bacterium, τ is a membranian tension.

A simple analogy of clothesline can help to understand what is happening. You need to pull more your clothesline to put more clothes on it. When you pull the rope by two ends you create a tension. More this tension is more weight (pressure) you can put on the rope.

All this will lead to establish the pressure difference at the tube extremities and we will get a Poiseuil flow. Constituents diluted in water will move from one cell to another unidirectionally and faster than simply diffusing. This is a fast process that we have named the "assisted diffusion"

When membranes behave like a 2D Van der Waals fluid

Trapped between the osmotic pressure and the cell wall, phospholipids particles are moving in a double layered environment. Their motion is constricted into a two dimensional motion, following the shape of the membrane. At the scale of the phospholipid, the motion can be approximated to a motion in 2D. Using statistical physics approach, we can say that the phase space has 4N dimensions: two dimensions of impulsion and two dimensions of coordinate for each particle(N is the number of particles in the system).

Can we describe the interaction between two phospholipids in the membrane? The question is complicated but we will demonstrate that by describing properly the phospholipid, it is reasonable to fit a Lennard-Jones potential energy to this interaction. The energy of binding is smaller and the speed of sliding of one phospholipid against another is slower than the internal vibration of the chemical bounds and the internal conformers rotation of the CH2 tails. Though, in Intermolecular Forces by Israelachvili(to be completed) the author shows that a phospholipid trapped in a bilayer can be aproximated by a section of cone. The section of cones is an individual, and the others are section of cone joining the previous one. The shape of the sections are giving the shape of the global structure.

Fig5: Chemical structure of one pholpholipid	Fig6: Schematics of the cylindrical approximation made for the phospholipid

Speaking in term of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a sterical repulsion keeps the molecules apart, and the hydropatic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients.

Is this phenomenon important? Back-of-the-envelope calculation

Let's start with a rough estimation of the flux transmitted through a nanotube. We assume that 5% of the surface area of one bacterium could be transmitted through the nanotube to a second bacterium. An order of magnitude of the transmitted surface is 10^-14 m². A nanotube of the radius 100 nm (that is the mean value of radius taken from the article) with this surface would be 0.5 µm long. The nanotubes observed in Dubey and Ben-Yehuda experiments were about 100 nm to 1 µm.

Let's take for example a tube 0.2 µm long. That means that 2.5*of the surface of the tube will be used in the process. We can imagine it splited in two stages: the first is the establishment of contact between two bacteria, for that 1 surface of the tube will be used. The remaining 1.5 surface of the tube will be used to transport the liquid inside the tube. As the diameter of the tube is of order of 100 nm, we can neglect the complexity of the fluid movement inside. In our model we will consider the fluid moving with the membrane. So the volume of transmitted liquid is about 10^-20 m³, whereas the cell volume is 5*10^-18 m³.

We consider then that some molecules are produced in the first cell and they are uniformally distributed. With 10'000 molecules in the first cell, we can expect about 200 molecules transmitted through one nanotube to another cell. That number of molecules seems to be sufficient to be detected.

The membrane tension calculation

Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the whole sphere surface per one phospholipid :

The caracteristic distance between two neighbor phospholipids on the membrane can be written like this :

where N is the number of phospholipids on the membrane. From this moment on we will work in canonical ensemble. The temperature is fixed and so is the number of particles in the system N. We also consider that the phospholipids can move only on the sphere surface that means that we will study the evolution of our system in 2N dimentional phase space. The partition function will look like :

where the Hamiltonian is :

Knowing the partition function is a great deal. We can derive a free energy

of each sphere, total free energy and the membranian tenstion from it :

For two spheres we get :

and

Back to the classical physics

To deduce the force exercising on the tube from membranian pressure, please refer to an explanation figure below :

The force calculation

Tension-force_explanation / The force applied to the nanotube as a function of the surface tension force.

Geometry / The system geometry.

Here T is a surface tension, N is a resulting force of the area of the tube attachment to the bacterium, Δα or α is the half of the angle with a vertex in the center of the bacterium and between the tube extremities. Only this zone is giving a non-compensated contribution to the resulting force.

So the force exercising on the tube is given by the formula :

where r is the tube radius, R is the bacterium radius.

At first approximation we can consider the process a serie of quasi equilibrium states, that it is rather slow that acceleration of the membrane is zero. We find the speed of the tube membrane at every moment of time out of the second Newton's law :

where ΔF is the difference of the forces applied to the extremities of the tube.

The number of phospholipids in two bacteria will change according to these equations :

where N1, N2 are numbers of phospholipids on the membrane of the first and the second bacterium corrispondingly, ΔS is the surface per one phospholipid one the tube.

Cutting the whole period of time of our process into laps of time dt we should solve the Poiseuille equation each time reevoluating the difference of pressure :

The Poiseuille equation :

where L is the total length of the nanotube, r is the distance from the center line of the nanotube, R is the radius of the nanotube.

The flow of the liquid passed through the nanotube is :

By integrating the last formula in time we will get the mass of the liquid passed from one bacterium to another :

where T is the time of the process which we can estimate like...

Getting the good parameters

We have done several simulations where the system consisted of two spherical bacteria of radius R1 and R2, the nanotube of the length L and the radius r between them, and the number of phospholipids N1 and N2 on them.

The nanotube dimentions we have taken from the article published by Dubey and Ben-Yehuda [1] (r = 100 nm, L = 1 µm). The ideas about what values to take for R1, R2 and N1, N2 we got from the bionumber's site. We have checked several sets of parameters :

• N1 = 2*10⁶, N2 = 1*10⁶, R1 = R2 = 1 µm;
• N1 = 2*10⁶, N2 = 1*10⁶, R1 = R2 = 1 µm;

Analysing the results

Can this process be an efficient way for passing molecules?

Conclusion