Our equations and how we obtained them

Toggle switch

1. Biological Models

A toggle switch consists of two genes, each coding for a protein that represses the expression of the other gene. This double repression system ensures the basic function of a toggle switch: a bistable system which can be switched from one state to the other by putting, in our example, some IPTG or aTc molecules in the medium.

The biological system we are trying to implement is more complex, on both the biological and physical side. However, the toggle switch model is basically the same. In the study of the toggle switch itself, the system can be reduced to a simple two-state subsystem that we will then use for the rest of our modelling. The toggle switch itself is not influenced by the rest of the system, if we do not consider the RsmA regulatory system that will be modeled at the very end of our work. Thus we will be able to model the toggle switch independently and then build the rest of the model upon this basis.

2. Mathematical Models

We use a common model for the toggle switch that we demonstrate below. The differential equation describing the production of TetR is as follows

$$\frac{d\left[\mathrm{TetR}\right]}{dt}=\frac{k_{\mathrm{plac}}\left[P_{\mathrm{lac\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{LacI}\right]}{K_{\mathrm{plac}}+\frac{K_{\mathrm{plac}}\left[\mathrm{IPTG}\right]}{K_{\mathrm{LacI\; -\; IPTG}}}}\right)}^{n_{\mathrm{plac}}}}-{\mathrm{\&;}}_{\mathrm{TetR}}\left[\mathrm{TetR}\right]$$

For better understanding of this model we demonstrated it. The differential equation describing the production of xR is as follow :

$$\frac{d\left[\mathrm{TetR}\right]}{dt}=k_{\mathrm{plac}}\left[P_{\mathrm{lac\; free}}\right]-{\delta }_{\mathrm{TetR}}\left[\mathrm{TetR}\right]$$

with [Plac free ] being the concentration of available binding sites - i.e. not repressed by LacI molecule. Plac_free is of course related to the total number of promoters Plac : $$\left[P_{\mathrm{lac\; free}}\right]+\left[P_{\mathrm{lac\; -\; LacI}}\right]=\left[P_{\mathrm{lac\; total}}\right]$$ with [Plac − LacI ] being the concentration of promoters repressed by LacI. If we set $K_{\mathrm{plac}}=\frac{\left[P_{\mathrm{lac\; free}}\right]\left[\mathrm{LacI}\right]}{\left[P_{\mathrm{lac\; -\; LacI}}\right]}$ we get : $$\left[P_{\mathrm{lac\; free}}\right]=\frac{\left[P_{\mathrm{lac\; total}}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{LacI}\right]}{K_{\mathrm{plac}}}}$$ We then try to get [LacI] : $$\left[\mathrm{LacI\; -\; IPTG}\right]+\left[{\mathrm{LacI}}_{\mathrm{free}}\right]+\left[\mathrm{LacI\; -\; plac}\right]=\left[\mathrm{LacI}\right]$$ with [LacI - IPTG] the concentration of LacI bound to IPTG and [LacI - plac ] the concentration of the complex of LacI and the promoter. If we set $K_{\mathrm{LacI\; -\; IPTG}}=\frac{\left[\mathrm{LacI}\right]\left[\mathrm{IPTG}\right]}{\left[\mathrm{LacI\; -\; IPTG}\right]}$ we get : $$\left[\mathrm{LacI}\right]=\frac{\left[{\mathrm{LacI}}_{\mathrm{total}}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{IPTG}\right]}{K_{\mathrm{LacI\; -\; IPTG}}}}$$ which finally gives our differential equations for TetR : $$\frac{d\left[\mathrm{TetR}\right]}{dt}=\frac{k_{\mathrm{plac}}\left[P_{\mathrm{lac\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{LacI}\right]}{K_{\mathrm{plac}}+\frac{K_{\mathrm{plac}}\left[\mathrm{IPTG}\right]}{K_{\mathrm{LacI\; -\; IPTG}}}}\right)}^{n_{\mathrm{plac}}}}-{\delta }_{\mathrm{TetR}}\left[\mathrm{TetR}\right]$$

The equation can be generalized to account for cooperativity arising from multimerization of the transcription factors, here represented by the cooperativity constant n_plac

In a similar way, we obtain a differential equation for LacI: $$\frac{d\left[\mathrm{LacI}\right]}{dt}=\frac{k_{\mathrm{pTet}}\left[P_{\mathrm{Tet\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{TetR}\right]}{K_{\mathrm{pTet}}+\frac{K_{\mathrm{pTet}}\left[\mathrm{aTc}\right]}{K_{\mathrm{TetR\; -\; aTc}}}}\right)}^{n_{\mathrm{pTet}}}}-{\delta }_{\mathrm{LacI}}\left[\mathrm{LacI}\right]$$

These two equations can be easily computed with a differential solver. We can precisely estimate the effects of each parameter.

Our equations and how we obtained them

Quorum sensing

1. Mathematical Models

Our work mainly refers to the models set up by the 2007 iGEM Bangalore team. On the basis of their work we set up models adapted to our own system. For these reasons we strongly recommend getting familiar with the works of the 2007 Bangalore team for an easier understanding of the models we used.
The main difference between our models is that their model is designed for a whole medium, in which the concen- trations of quorum sensing molecules are considered for a whole fixed volume of a medium. Our system, however, is supposed to describe the spatial diffusion of quorum sensing molecules as well, and therefore needs to be designed for an infinitesimal volume of medium containing bacteries and outside medium. A few other differences exist between our model and theirs, mainly due to the fact that the system we intend to describe is made of other different parts. For example the production rate of our Quorum Sensing enzymes are directly linked to the previously described toggle switch model.

For these reasons we strongly recommend getting familiar with the works of the 2007 Bangalore team for an easier understanding of the models we used.

Bangalore 07 modeled the behaviour of quorum sensing for a simple quorum sensing system. With the input of the toggle switch model taken into account, we can adapt their equations to our system. With our toggle switch system the production would be ruled by the regulatory network of LacI and TetR :

$$\frac{d\left[\mathrm{CinI}\right]}{dt}=\frac{k_{\mathrm{pTet}}\left[P_{\mathrm{Tet\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{TetR}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{aTc}\right]}{K_{\mathrm{TetR\; -\; aTc}}}}\right)}^{n_{\mathrm{pTet}}}}-{\delta }_{\mathrm{CinI}}\left[\mathrm{CinI}\right]$$ $$\frac{d\left[{\mathrm{CinR}}_{\mathrm{free}}\right]}{dt}=\frac{k_{\mathrm{plac}}\left[P_{\mathrm{lac\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{LacI}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{IPTG}\right]}{K_{\mathrm{LacI\; -\; IPTG}}}}\right)}^{n_{\mathrm{plac}}}}-{\delta }_{\mathrm{CinR}}\left[{\mathrm{CinR}}_{\mathrm{free}}\right]-V_{\mathrm{complexation}}$$

We can therefore describe the production of CinI and CinR_free inside the cells. V_complexation is the complexation rate of CinR_free with AHL molecule. As a matter of fact CinR will be transformed into CinR* after being complexed with the Quorum Sensing molecules entering the cell. It is now taken into account via this complexation rate.
A simple way to write this rate would be as follow : $$V_{\mathrm{complexation}}=k_{\mathrm{comp}}{Q}_i^n\left[{\mathrm{CinR}}_{\mathrm{free}}\right]$$ with Qi being the concentration in QS molecule inside the cell. If we consider that only one QS molecule would bind to a CinR molecule, we obtain the following equation for CinR : $$\frac{d\left[{\mathrm{CinR}}_{\mathrm{free}}\right]}{dt}=\frac{k_{\mathrm{plac}}\left[P_{\mathrm{lac\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{LacI}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{IPTG}\right]}{K_{\mathrm{LacI\; -\; IPTG}}}}\right)}^{n_{\mathrm{plac}}}}-{\delta }_{\mathrm{CinR}}\left[{\mathrm{CinR}}_{\mathrm{free}}\right]-k_{\mathrm{comp}}{Q}_i^{}\left[{\mathrm{CinR}}_{\mathrm{free}}\right]$$

For the following equations the physical volume considered is an infinitesimal volume of medium along x - i.e. we only consider an l ∗ dx volume of cell, l being the width of our plate and dx an infinitesimal portion of length. In this infinitesimal volume we set a fixed number of non-growing cells and take into account the diffusion from one portion to the next ones.

$$\frac{d\left[\mathrm{Qi}\right]}{dt}=\eta \left(\left[\mathrm{Qe}\right]-\left[\mathrm{Qi}\right]\right)-{\delta }_{\mathrm{Qi}}\left[\mathrm{Qi}\right]+\mathrm{f([CinI])}$$ $$\frac{d\left[\mathrm{Qe}\right]}{dt}=\rho v_c\eta \left(\left[\mathrm{Qi}\right]-\left[\mathrm{Qe}\right]\right)-{\delta }_{\mathrm{Qe}}\left[\mathrm{Qe}\right]+D_{\mathrm{diff}}\frac{{\∂}^2\left[\mathrm{Qe}\right]}{\∂x^2}$$
• With f ([CinI]) being a mathematical function describing the production of QS molecule by CinI enzyme. Basically this fonction would be as follow :
$$\mathrm{f([CinI])\; =}{k}_{{\mathrm{QS}}_p}{\left[\mathrm{substrate}\right]}^n\left[\mathrm{CinI}\right]$$ But if this reaction is assumed first-order, we obtain : $$\frac{d\left[\mathrm{Qi}\right]}{dt}=\eta \left(\left[\mathrm{Qe}\right]-\left[\mathrm{Qi}\right]\right)-{\delta }_{\mathrm{Qi}}\left[\mathrm{Qi}\right]+k_{{\mathrm{QS}}_p}^{\text{'}}\left[\mathrm{CinI}\right]$$
• With Ddiff being the diffusion coefficient for our Quorum sensing molecule in our medium along spatial dimension x.
• In our case ρvc is a constant (we consider the cells do not grow in our time scale)

With the equations set (3.1); (3.3); (3.5); (3.6) we have, we can not use solvers like matlab ODE because of their space and time dependancies. To solve our problem we have to use a space-time derivation matrix we will describe in the next chapter.

2. Solvation ot the set of equations (3.1); (3.3); (3.5); (3.6)

3. To solve this set of equations we have to use a matrix that will describe our system in both space and time. for example for the QS molecule outside of the cell :

   $$M_{Q_e}\left(\mathrm{m,n}\right)=\left[Q_e\right]\left(\mathrm{x,t}\right)$$ $$M_{Q_e}\left(\mathrm{m+1,n+1}\right)=\left[Q_e\right]\left(\mathrm{x+dx,t+dt}\right)$$
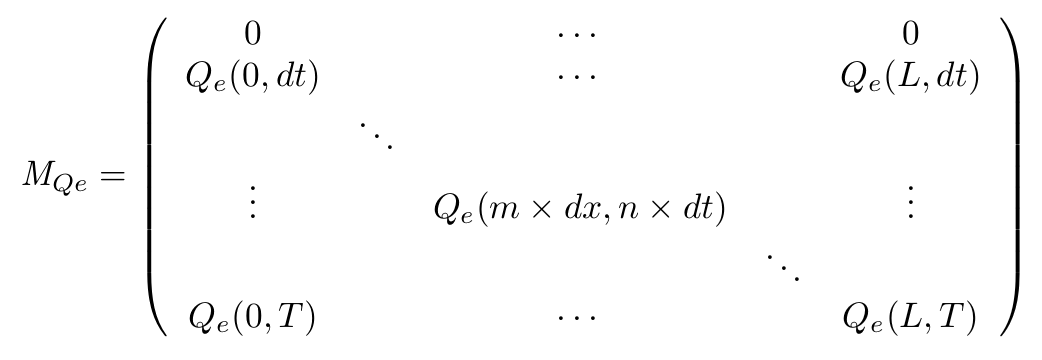
   • On the spatial point of view, we only consider the x dimension, as the IPTG gradient will be only evolving along this dimension. Thus we consider the state of our cells is the same along the width of our plate.
   • With this Matrix, and after computation of all the terms, we can get the entire behaviour of CinI, CinR, QS inside and outside the cells.
   • The first line of the Matrix equals 0. These are the initial conditions we set to 0 at time t = 0s.
   • On the borders of the plate (x = 0 and x = L) the model used has to be different, limit conditions will be set.
   • Of course, Qi, CinI and CinR matrices will be similarly implemented.

   With our continuous equations set, we want to obtain discrete definition of each of the matrices. The interdepen- dancies of the equations imply that the computation of the matrices will be performed on the entire CinI matrix first, then each line of the Qi and Qe matrices will be computed alternatively. Finally CinR matrix computation will be performed.

   Parallel computation of all the matrices without proper control is not possible indeed, as the terms of Qi matrix will depend on the Qe terms of the preceding line (and vice-versa). Discretization is obtained with first order taylor series :

   $$M_{Q_i}\left(\mathrm{m,n+1}\right)=\Delta t\left(\eta \left(M_{Q_e}\mathrm{(m,n)}-M_{Q_i}\left(\mathrm{m,n}\right)\right)-{\delta }_{Q_i}{M}_{Q_i}\left(\mathrm{m,n}\right)+k_{{\mathrm{QS}}_p}{M}_{\mathrm{CinI}}\left(\mathrm{m,n}\right)+M_{Q_i}\left(\mathrm{m,n}\right)\right)$$ $$M_{Q_e}\left(\mathrm{m,n+1}\right)=\Delta t\left(D_m+D_{\mathrm{diff}}\frac{M_{Q_e}\left(\mathrm{m+1,n}\right)-{\mathrm{2M}}_{Q_e}\left(\mathrm{m,n}\right)+M_{Q_e}\left(\mathrm{m-1,n}\right)}{}\right)-M_{Q_e}\left(\mathrm{m,n}\right)$$

   with $D_m=\rho v_c\eta M_{Q_i}\left(\mathrm{m,n}\right)-M_{Q_e}\left(\mathrm{m,n}\right)\left({\delta }_{Q_e}+\rho v_c\eta \right)$

   $$M_{\mathrm{CinR}}\left(\mathrm{m,n+1}\right)=\Delta t\left(\frac{k_{\mathrm{pTet}}\left[P_{\mathrm{Tet\; total}}\right]}{\mathrm{1\; +}{\left(\frac{\left[\mathrm{TetR}\right]}{\mathrm{1\; +}\frac{\left[\mathrm{aTc}\right]}{K_{\mathrm{TetR\; -\; aTc}}}}\right)}^{n_{\mathrm{pTet}}}}-M_{\mathrm{CinR}}\left(\mathrm{m,n}\right)\left({\delta }_{\mathrm{CinR}}-k_{\mathrm{comp}}{M}_{Q_i}\left(\mathrm{m,n}\right)\right)\right)+M_{\mathrm{CinR}}\left(\mathrm{m,n}\right)$$

With these discrete equations the 4 matrices can be computed through simple calculation loops over each line. The CinI matrix does not depend on space dimension, it is then possible to compute it without discretization with a differential solver.

Our algorithms

In the MATLAB archive that can be found here containing our matlab scripts for deterministic modelling (file Deterministic_archive.tar.gz) you can launch an ODE based simulation (see our ODEs in the two previous sections) with the file biosenseur1Dmain.m.

Several dialog boxes will pop up to enter the specificities of the simulation : (physical specificities of the device, chemical species concentrations and IPTG gradient )

At the end of the simulation you obtain 3 matrices named M_stock, M_QS and M_comp containing the concentrations in each protein species at each time point and on each physical point of the plate. We wrote three MATLAB scripts that display the concentration in proteins dynamically that you can call with DynamicplottingTS, DynamicplottingQS and DynamicplottingCP. For a good understanding of the models and of our results we also wrote a script to illustrate the coloration of our plate through time according to our models named Imageshow.m.