Team:Edinburgh/Cellulases (MATLAB model)
From 2011.igem.org
(→Results) |
|||
| Line 9: | Line 9: | ||
MATLAB is a general-purpose mathematical tool, developed by [http://www.mathworks.com Mathworks], and commonly used by engineers. Among other things, it can be used to solve ordinary differential equations (ODE's) by numerical integration. | MATLAB is a general-purpose mathematical tool, developed by [http://www.mathworks.com Mathworks], and commonly used by engineers. Among other things, it can be used to solve ordinary differential equations (ODE's) by numerical integration. | ||
| - | An attempt was made to use MATLAB to model the degradation of <span class="hardword" id="cellulose">cellulose</span> into glucose in a biorefinery. But accurately predicting how much is converted in the <span class="hardword" id="synergy">synergistic</span> system (where enzymes are kept close together) is difficult without literature to provide the | + | An attempt was made to use MATLAB to model the degradation of <span class="hardword" id="cellulose">cellulose</span> into glucose in a biorefinery. But accurately predicting how much is converted in the <span class="hardword" id="synergy">synergistic</span> system (where enzymes are kept close together) is difficult without literature to provide the ODEs and the kinetic parameters. Therefore this model only looks at the free floating (non-synergistic) enzyme approach. It is <span class="hardword" id="deterministic">deterministic</span> and is set by a series of initial conditions. |
==Assumptions== | ==Assumptions== | ||
Revision as of 12:19, 14 September 2011
Cellulases (MATLAB model)
MATLAB is a general-purpose mathematical tool, developed by [http://www.mathworks.com Mathworks], and commonly used by engineers. Among other things, it can be used to solve ordinary differential equations (ODE's) by numerical integration.
An attempt was made to use MATLAB to model the degradation of cellulose into glucose in a biorefinery. But accurately predicting how much is converted in the synergistic system (where enzymes are kept close together) is difficult without literature to provide the ODEs and the kinetic parameters. Therefore this model only looks at the free floating (non-synergistic) enzyme approach. It is deterministic and is set by a series of initial conditions.
Contents[hide] |
Assumptions
The mathematical model is based on the ODE's and kinetic parameters outlined in [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Kadam et al (2004)]. The following are its assumptions and basis:
- Underlying assumption: cellulose, cellobiose, and glucose concentrations change continuously with time.
- Rate equations assume enzyme adsorption follows the Langmuir isotherm model.
- Glucose and cellobiose, which are the products of cellulose hydrolysis, are assumed to "competitively inhibit enzyme hydrolysis".
- All reactions are assumed to follow the same temperature dependency Arrhenius relationship (shown below). However, in reality it should be different for every enzyme component, "because of their varying degrees of thermostability, with β-glucocidase being the most thermostable. Hence the assumption is a simplification of reality".
- Conversion of cellobiose to glucose follows the Michaelis-Menten enzyme kinetic model.
Equations
Rate Equations
Constants
- knr — reaction rate constant for reaction n
- EnB — the bound concentration for exo and endo-β-1,4-glucanase for reaction n
- Rs — substrate reactivity parameter
- S — substrate reactivity at a given time (g/kg)
- G2 — concentration of cellobiose
- G — concentration of glucose
- X — xylose concentration
- KnIG2 — inhibition constant for cellobiose at reaction n
- KnIG — inhibition constant for glucose at reaction n
- KnIX — xylose inhibition constant for reaction n
Note: For simplicity's sake we have assumed no xylose in the system, therefore X=0.
Langmuir Isotherm

Constants
- exo and endo-β-1,4-glucanase, i=1
- β-glucosidase, i=2
- Eimax — Maximum mass of enzyme that can be absorbed onto a unit of mass substrate
- Kiad — Dissociation constant for enzyme i
- EiF — Free enzyme concentration for enzyme i
- S — Substrate reactivity at a given time (g/kg)
Mass Balances
Arrhenius Equation
Constants
- Kir — Reaction rate constant of reaction i
- Eai — Activation energy of reaction i
- R — Universal gas constant
Construction of Model
The model was constructed using the numerical programme MATLAB. A script file was generated which holds the variable dictionary, constants, temperature dependency equations, the "ODE45" differential equation solver, and the plot command.
A separate function file to the script is created as script files can only operate on the variables that are coded into their m-files. Rs (the substrate reactivity parameter) changes at every iteration because it is dependent on the S the substrate concentration at a given time, the substrate being cellulose. Therefore S at the first iteration is S0, the initial substrate concentration. At the second iteration S is the previous value calculated by the ODE, and so on. After each step the new value of S is fed into the function file and is used for calculating the reaction rate constant for cellobiose and glucose, etc.
ODE45 calls on the function file to calculate the rate equations and then substitute them into the respective mass balance. A numerical integration is performed and the results can be seen below. ODE45 is used as it is more accurate than other solvers [http://www.mathworks.co.uk/help/techdoc/ref/ode23.html (according to Mathworks)]. It is based on an explicit Runge-Kutta formula and is a one-step solver.
Results
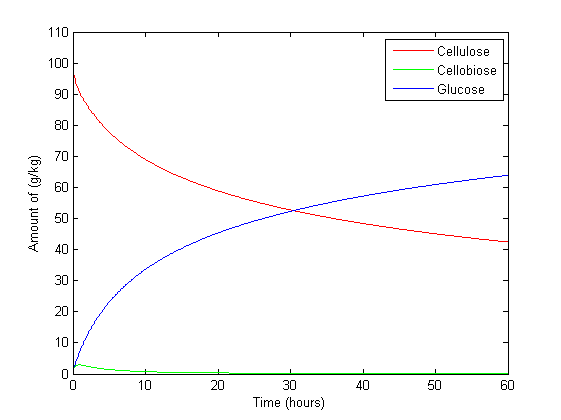
Figure 1 is set with β-glucosidase at its maximum concentration and Figure 2 with Exo/endo-glucanase at maximum. This is to compare the effect of certain enzymes on cellulose degradation and glucose production. The result is consistent with what is expected. Exoglucanase chews away at the end of a cellulose chain, producing cellobiose sugars and endoglucanase cuts cellulose chanins in the centre, turning one chain into two. This concurs with the results, with Figure 2 modelling markedly higher amount of cellulose at the maximum amount of exo/endo-glucanase than that of Figure 1. Whereas β-glucosidase cuts cellobiose in half, producing two glucose molecules. Figure 1 which β-glucosidase is at its maximum produces 167% more glucose than in Figure 2 with β-glucosidase at its minimum at steady state.
Cellobiose in Figure 1 increases to 10 g/kg in 20 hours but after 50 hours begins to decrease. This is because β-glucosidase starts to convert it to glucose. This result cannot be seen in Figure 2 with little β-glucosidase present in the system as a result cellobiose increases to 60 g/kg.
Figure 3 is under the same conditions as Figure 1, but its x-axis is set to a semilog scale to illustrate what happens over a longer period of time. The effect of high β-glucosidase can better be seen with the complete conversion of cellobiose to glucose.
Interestingly, the amount of glucose over time highlights one of the limitations of an ODE based model. The amount of glucose increases beyond the amount of cellulose present initially, which breaks the law of conservation of mass. And the amount of cellobiose present becomes negative. This is caused by MATLAB's continuous iterations, which don't stop at any point in time. Neither glucose nor cellobiose reach a stable steady state. The ODE has limits within which it works best. By contrast, an agent-based model, such as our Kappa model, explicitly tracks individual sugar molecules and so avoids this problem.
Download MATLAB file
You can download the ready model as a .zip file:

References
- Kadam KL, Rydholm EC, McMillan JD (2004) [http://onlinelibrary.wiley.com/doi/10.1021/bp034316x/full Development and Validation of a Kinetic Model for Enzymatic Saccharification of Lignocellulosic Biomass]. Biotechnology Progress 20(3): 698–705 (doi: 10.1021/bp034316x).
 "
"