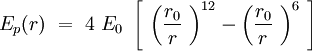Team:Paris Bettencourt/Modeling/Assisted diffusion
From 2011.igem.org
(→Let's start the Maths) |
(→Let's start the Maths) |
||
| Line 82: | Line 82: | ||
where N is the number of phospholipids on the membrane. | where N is the number of phospholipids on the membrane. | ||
| + | From this moment on we will work in canonical ensemble. The temperature is fixed and so is the number of particles in the system N. We also consider that the phospholipids can move only on the sphere surface that means that we will study the evolution of our system in 2N dimentional phase space. | ||
| + | |||
| + | The partition function will look like : | ||
| + | |||
| + | [[File:Partition_function.png|center|Partition function in canonical ensemble]] | ||
| + | |||
| + | where the Hamiltonian is : | ||
| + | |||
| + | [[File:Hamiltonian.png|center|Hamiltonian of the system]] | ||
Revision as of 23:03, 11 September 2011

Contents |
Introduction to the model
The diffusion through the nanotubes is a fast process. This speed can be partially explained by the passive diffusion through the tubes. But what if it is faster? The article from Dubey and Ben-Yehuda suggests that the diffusion is an active process. Several points can be opposed to this statement:
- First, the diffusion is happening with molecule of different natures, that have nothing to do with the natural compoments of a cell
- Unlike the mamalian cells, the tube seems not to have no "railroad" design for such a transport
The question is: can we immagine a process that is faster than passive diffusion but does not rely on specific interractions?
The answer is probably yes, and in this page we propose a new model, really challenging for the mind, but that can play a role in the diffusion process through the nanotubes.
General physical concepts and Hypothesis
Starting from an analogy
Immagine two bottles of gaz connected by a tube. The fist one have an higher pressure than the second one. In the first one, diluted in the gaz, there are a few molecules of another nature. We follow the destiny of these molecules.
When you open the tape, the bottle with a higher pressure will equillibrate with the other one my moving a certain quantity of it's particles through the tube in the direction of the second bottle. These moving molecules will drag with them the copoment diluted in the gaz and a few of these molecules will be transported to the other bottle.
From the analogy to the biology
Of cource, the cell is not a bag of liquid under pressure. The water is equillibrated at both sides of the exterior membrane. The pressure we are dealing with is not related to water or osmotic pressure (that is a "passive diffusion thermodynamical pressure"). There is a part of the cell we are not used to think about that undergo a huge variablilty of pressure: the phospholipid membrane!
Let's evaluate the constraints that the membrane underdo. First, as it is a Gramm positive bacteria, the external sugar envelopp impose the shape of the bacteria. On the other hand, the osmotic pressure is pushing the membrane against the sugar wall. Inside the membrane, the number of phospho-lipids is fixed by the state of division on the cell.
Though, a phospholipid is somehow behaving as a gaz trapped in a bottle. The ospotic pressure and the sugar layer are the bottle, and the number of particle trapped is giving the pressure. This variation of pression can be important if the cell has just devide or if the cell is about to devide.
 |
 |
The tube is small and water has its intrinsic viscosity. If the pipe is moving, the water inside will follow, pumping the water from one cell to another. The sliding will look like a Poiseuil flow. Constituents diluted in water will move from one cell to another unidirectionally and faster than simply diffusing. This is a fast process that we have named after the "active" and "passive" diffusion, the "assisted diffusion"
When membranes behave like a 2D Van der Waals fluid
Trapped between the osmotic pressure and the cell wall, the phospholipids particle are moving in a double layered environement. Their motion is contricted into a two dimentional motion, following the shape of the membrane. At the scale of the phospholipid, the motion can be approximated to a motion in 2D. Using the formalism of the Statistical Physics, we can say that the phase space has 4 dimentions: two dimentions of impulsion and two dimentions of coordinate.
Can we descripe the interraction between two phospholipids in the membrane? Well, the question is complicated, but we will demonstrate that describing properly the pholpholipid, it is reasonable to fit a Lennard-Jones potential energy to this interraction. The enery of binding is smaller and the speed of sliding of one phospholipid against another is slower than the internal vibration of the chemical bounds and the internal conformers rotation of the CH2 tails. Though, in Intermolecular Forces by Israelacviili, the author shows that a phospholipid trapped in a bilayer can be aproximated by a section of cone. The section of cones is an individual, and the others are section of cone joining the previous one. The shape of the sections are giving the shape of the global structure.
 |
 |
Speaking in term of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interraction. If the cones are interpenetrating, a sterical repulsion keeps the molecules appart, and the hydropatic interraction that joins one lipid with the other act as an attractive force keeping the coherence of the mombrane. We will discuss later about the value of the two coefficients.
Let's start the Maths
Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the hole sphere surface per one phospholipid :
The caracteristic distance between two neighbor phospholipids on the membrane can be written like this :
where N is the number of phospholipids on the membrane.
From this moment on we will work in canonical ensemble. The temperature is fixed and so is the number of particles in the system N. We also consider that the phospholipids can move only on the sphere surface that means that we will study the evolution of our system in 2N dimentional phase space.
The partition function will look like :
where the Hamiltonian is :
In stastical physics, in the canonic ensemble, the partition function for a classical particule is given by:
Where H(p,r) is the Hamiltonian of the system, given by:
where LJ(r1,r2) is the potential energy given by the Lennard Jones formulea. As usual in statiscical physics, we devide the total potential energy of the system into the pair-to-pair interraction between particles.
Once calculated, the partition function has the form of:
The next step is to calculate the free-energy associated with the partition function. Free energy is the value that links the statiscical physics to classical thermodynamics. The classical formulea is:
Which, once applicated to our system gives:
The pressure of the membrane, that correspond to the tension, is given by the formulea
... ...
And so on Oleg !!!
... ...
Which gives a tension that is a function of the radius of the vesicle (R), the number of lipids (N) and the temperature (T)
Back to the classical physics
Now that we can calculate the tension of the membrane (i.e. the pressure of the Wan der Waals fluid), we can start calculating the equential equation of the relaxation of the membrane. As it is a fluid with an intrinsic viscosity, we will use the Navier-Stokes equation.
Let's first choose a point of view of considering the flux. There is the Bernouilli point of view in which we track the fluid particule destiny and the stokes point of view in which we are fixed in one point and watch the flux of fluid particle. The second point of view is easier for us, because, we want to count in the end the a certain quantity of phopholipids that have passed through the tubes, and link that to the quantity of water.
Let's imagine that we are an observer sitting at the entrance of the nanotube. He watch the liquid passing between his legs, and canlculate the flux.
... ...
Your job agains Oleg, the games get it's tracks!!
... ...
Finally with a difference of pressure P2-P1, we can estimate the caracteristical time of the relaxation to be:
where...
Getting back to the quantity of water
We are in the situation where a tube, that have good hydrophilic properties is moving, the tube is small and the liquid viscuous (the density of the cytoplasm over the tensity of water is about 3.2). Water will be dragged in the tube.The fluid will undergo a Poiseuille flow, but this time the tube is moving and the water following.
... ...
Going down the Poiseuille equation you will estimate the total flux dragged for a certain quantity of phospholipids that have passed bhy depending on the size of the tube, the viscosity of water...
... ...
Getting the good parameters
It will take some time, but once you have the equation, from the size of a vesible in equillibium, when we know the number of phospholipids. The viscosity has probably been estimated by FRAP techniques. For the rest, we will find out.
Analysing the results
Can this process be an efficient way for passing molecules??
Conclusion
 "
"