Team:Imperial College London/Project/Chemotaxis/Results
From 2011.igem.org
| Line 106: | Line 106: | ||
<p>mainly by diffusion, biased motion with the presence of chemoattractant<br /> | <p>mainly by diffusion, biased motion with the presence of chemoattractant<br /> | ||
based on the malate distribution in steady-state and the Spiro model</p> | based on the malate distribution in steady-state and the Spiro model</p> | ||
| - | |||
</body> | </body> | ||
| - | |||
<h2>28th of July</h2> | <h2>28th of July</h2> | ||
<p>-We have made tryptone broth, which will be used to grow E. coli (K-12 D10b strain) overnight before the chemotaxis<br> experiments, for them to develop flagella and therefore they will be capable of chemotaxis. To make tryptone broth look <br>at protocols. </p> | <p>-We have made tryptone broth, which will be used to grow E. coli (K-12 D10b strain) overnight before the chemotaxis<br> experiments, for them to develop flagella and therefore they will be capable of chemotaxis. To make tryptone broth look <br>at protocols. </p> | ||
| Line 360: | Line 358: | ||
<b>Capillary assay</b> | <b>Capillary assay</b> | ||
<p> quantitative, bacterial movement into a syringe/capillary based on attraction, number of bacteria measured in a capillary after 30min using FACS machine. motility medium & high bacterial OD used..</p> | <p> quantitative, bacterial movement into a syringe/capillary based on attraction, number of bacteria measured in a capillary after 30min using FACS machine. motility medium & high bacterial OD used..</p> | ||
| - | + | <p>E.coli is a motile strain of bacteria, which is to say it can swim. It is able to do so by rotating its flagellum, which is a rotating tentacle like structure on the outside of cell. | |
| - | + | ||
| - | + | ||
| - | + | ||
Chemotaxis is the movement up concentration gradient of chemoattractants (i.e. malate in our project) and away from poisons. E.coli is too small to detect any concentration | Chemotaxis is the movement up concentration gradient of chemoattractants (i.e. malate in our project) and away from poisons. E.coli is too small to detect any concentration | ||
gradient between the two ends of itself, and so they must randomly head in any direction and then compare the new chemoattractant concentration at new point to the previous | gradient between the two ends of itself, and so they must randomly head in any direction and then compare the new chemoattractant concentration at new point to the previous | ||
| Line 399: | Line 394: | ||
<td width="205" valign="top"><p>Initial bacterial concentration</p></td> | <td width="205" valign="top"><p>Initial bacterial concentration</p></td> | ||
<td width="205" valign="top"><p>b0</p></td> | <td width="205" valign="top"><p>b0</p></td> | ||
| - | <td width="205" valign="top"><p> | + | <td width="205" valign="top"><p>108 cells/ml</p></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td width="205" valign="top"><p>Initial attractant concentration</p></td> | <td width="205" valign="top"><p>Initial attractant concentration</p></td> | ||
<td width="205" valign="top"><p>s0</p></td> | <td width="205" valign="top"><p>s0</p></td> | ||
| - | <td width="205" valign="top"><p>0. | + | <td width="205" valign="top"><p>0.1 mM or 0.1 mol/m3</p></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td width="205" valign="top"><p>Bacterial diffusion coefficient</p></td> | <td width="205" valign="top"><p>Bacterial diffusion coefficient</p></td> | ||
<td width="205" valign="top"><p>µ</p></td> | <td width="205" valign="top"><p>µ</p></td> | ||
| - | <td width="205" valign="top"><p>1.5*10- | + | <td width="205" valign="top"><p>1.5*10-5 cm2/s</p></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td width="205" valign="top"><p> | + | <td width="205" valign="top"><p>Bacterial chemotactic coefficient</p></td> |
<td width="205" valign="top"><p>χ</p></td> | <td width="205" valign="top"><p>χ</p></td> | ||
| - | <td width="205" valign="top"><p>1.5-75*10- | + | <td width="205" valign="top"><p>1.5-75*10-5 cm2/s</p></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td width="205" valign="top"><p>Attractant diffusion coefficient</p></td> | <td width="205" valign="top"><p>Attractant diffusion coefficient</p></td> | ||
<td width="205" valign="top"><p>D</p></td> | <td width="205" valign="top"><p>D</p></td> | ||
| - | <td width="205" valign="top"><p>10- | + | <td width="205" valign="top"><p>10-5 cm2/s</p></td> |
</tr> | </tr> | ||
</tbody> | </tbody> | ||
| Line 429: | Line 424: | ||
<ul> | <ul> | ||
<li>The entire root system is assumed to take the shape of a long cylinder. Hence, a cylindrical coordinate system will be used.</li> | <li>The entire root system is assumed to take the shape of a long cylinder. Hence, a cylindrical coordinate system will be used.</li> | ||
| - | <li>The system is axisymmetric and there is no variation along the vertical length of the root. Hence, | + | <li>The system is axisymmetric and there is no variation along the vertical length of the root. Hence, <img src="https://static.igem.org/mediawiki/2011/e/ea/ICL_EqnMalate3.png" alt="" width="72" height="28" /></li> |
| - | <li>The system has reached steady state and is time-independent. Hence, | + | <li>The system has reached steady state and is time-independent. Hence, <img src="https://static.igem.org/mediawiki/2011/4/48/ICL_EqnMalate4.png" alt="" width="72" height="28" /></li> |
<li>Degradation of chemoattractant is first order and is described by f = ks where k is the degradation rate of the chemoattractant.</li> | <li>Degradation of chemoattractant is first order and is described by f = ks where k is the degradation rate of the chemoattractant.</li> | ||
<li>Bacterial cell growth and death are neglected. Hence, g(b,s) = h(b,s) = 0</li> | <li>Bacterial cell growth and death are neglected. Hence, g(b,s) = h(b,s) = 0</li> | ||
</ul> | </ul> | ||
<p> Applying the assumptions above, equation (1) becomes</p> | <p> Applying the assumptions above, equation (1) becomes</p> | ||
| - | <p><img src="https://static.igem.org/mediawiki/2011/d/d7/ICL_EqnMalate5.png" alt="" width="131" height="29" /> | + | <p><img src="https://static.igem.org/mediawiki/2011/d/d7/ICL_EqnMalate5.png" alt="" width="131" height="29" /> </p> |
<p> Rearranging,<br /> | <p> Rearranging,<br /> | ||
| - | <img src="https://static.igem.org/mediawiki/2011/f/f1/ICL_EqnMalate6.png" alt="" width="119" height="30" /> | + | <img src="https://static.igem.org/mediawiki/2011/f/f1/ICL_EqnMalate6.png" alt="" width="119" height="30" /> -------------------------------------------------(3)<br /> |
Equation (3) is in the form of the modified Bessel equation. Hence, the solution of equation (3) is given by,<br /> | Equation (3) is in the form of the modified Bessel equation. Hence, the solution of equation (3) is given by,<br /> | ||
| - | <img src="https://static.igem.org/mediawiki/2011/3/3c/ICL_EqnMalate7.png" alt="" width="186" height="42" /> | + | <img src="https://static.igem.org/mediawiki/2011/3/3c/ICL_EqnMalate7.png" alt="" width="186" height="42" /> <br /> |
Where K0 is the modified Bessel function.<br /> | Where K0 is the modified Bessel function.<br /> | ||
Since it is unrealistic for the concentration to increase to infinity, A=0. And applying the boundary condition, the solution becomes,<br /> | Since it is unrealistic for the concentration to increase to infinity, A=0. And applying the boundary condition, the solution becomes,<br /> | ||
| - | <img src="https://static.igem.org/mediawiki/2011/f/fa/ICL_EqnMalate8.png" alt="" width="103" height="42" /> | + | <img src="https://static.igem.org/mediawiki/2011/f/fa/ICL_EqnMalate8.png" alt="" width="103" height="42" /> -----------------------------------------------------(4)</p> |
<p>The modeling result show that the steady-state pattern of malate distribution. The concentration of malate is a variable against the distance</p> | <p>The modeling result show that the steady-state pattern of malate distribution. The concentration of malate is a variable against the distance</p> | ||
<p><img src="https://static.igem.org/mediawiki/2011/1/14/ICL_Malate1.png" alt="" width="331" height="260" /> <img src="https://static.igem.org/mediawiki/2011/2/2f/ICL_Malate2.png" alt="" width="303" height="270" /></p> | <p><img src="https://static.igem.org/mediawiki/2011/1/14/ICL_Malate1.png" alt="" width="331" height="260" /> <img src="https://static.igem.org/mediawiki/2011/2/2f/ICL_Malate2.png" alt="" width="303" height="270" /></p> | ||
| Line 451: | Line 446: | ||
<li>the signal transfer inside the bacterium<br/> | <li>the signal transfer inside the bacterium<br/> | ||
chemoattractant stimulation -> chemoreceptor -> CheA -> CheY-P -> flagellar motor -> changed switching frequency between swimming and tumbling (biasing fraction)</li> | chemoattractant stimulation -> chemoreceptor -> CheA -> CheY-P -> flagellar motor -> changed switching frequency between swimming and tumbling (biasing fraction)</li> | ||
| - | <li>the phosphrylation level of CheY can indicate the signal transferring pathway, the CheY-P concentration | + | <li>the phosphrylation level of CheY can indicate the signal transferring pathway, the CheY-P concentration increases when the chemoreceptor is triggered</li> |
| - | <li>the modeling result will show the optimal concentration to trigger the chemoreceptors | + | <li>the modeling result will show the optimal concentration to trigger the chemoreceptors (10-6 mol/L)</li> |
</ul> | </ul> | ||
<p>high = saturated chemoreceptors<br /> | <p>high = saturated chemoreceptors<br /> | ||
| Line 464: | Line 459: | ||
<p>mainly by diffusion, biased motion with the presence of chemoattractant<br /> | <p>mainly by diffusion, biased motion with the presence of chemoattractant<br /> | ||
based on the malate distribution in steady-state and the Spiro model</p> | based on the malate distribution in steady-state and the Spiro model</p> | ||
| - | |||
</body> | </body> | ||
</html> | </html> | ||
Revision as of 12:43, 4 September 2011
Chemotaxis Results
Modelling
Two main aspects were modelled for our chemotaxis module: malate distribution in soil and the threshold concentration of malate needed to trigger chemotaxis.
The malate concentration distribution was modelled using the Keller-Segel model.
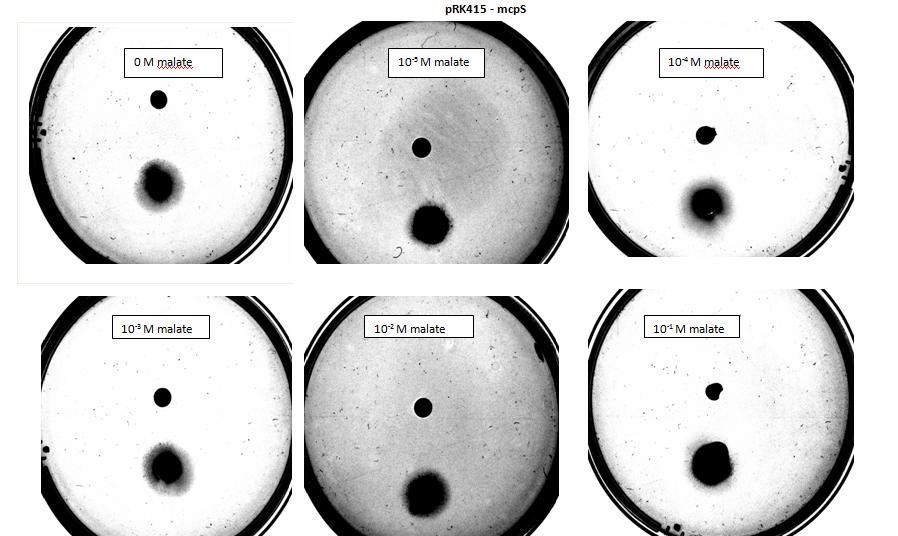
E.coli is a motile strain of bacteria, which is to say it can swim. It is able to do so by rotating its flagellum, which is a rotating tentacle like structure on the outside of cell. Chemotaxis is the movement up concentration gradient of chemoattractants (i.e. malate in our project) and away from poisons. E.coli is too small to detect any concentration gradient between the two ends of itself, and so they must randomly head in any direction and then compare the new chemoattractant concentration at new point to the previous 3-4s point. Its motion is described by ‘runs’ and ‘tumbles’, runs refer to a smooth, straight line movement for a number of seconds, while tumble referring to reorientation of bacteria [1]. Chemoattractant increases transiently raise the probability of ‘tumble’ (or bias), and then a sensory adaptation process returns the bias to baseline, enabling the cell to detect and respond to further concentration changes. The response to a small step change in chemoattractant concentration in a spatially uniform environment increase the response time occurs over a 2- to 4- s time span [2]. Saturating changes in chemoattractant can increase the response time to several minutes.
Malate concentration distribution
For our project, malate is the chemoattractant that results in the movement of E.coli. In this section, we will first model the concentration distribution of the chemoattractant, malate in the soil. Then, we will model the bacteria concentration pattern as a result of this distribution of malate. Finally, we will infer some useful information by analysing the results of the modelling.
We will model the concentration distributions of malate and bacteria using the Keller-Segel model which is governed by the two equations shown below. Solving the equations will give the concentration distributions of the malate and the bacteria respectively
 ---------------------------------------------------------------------------------------------(1)
---------------------------------------------------------------------------------------------(1)
 -------------------------------------------------------(2)
-------------------------------------------------------(2)
s = concentration of chemoattractant
D = diffusion coefficient of chemoattractant
f = degradation of chemoattractant
b = number concentration of bacteria
µ = bacterial diffusion coefficient (how fast bacteria spread)
χ = chemotactic coefficient (how sensitive bacteria are)
g = bacterial cell growth
h = bacterial cell death
The values of the above parameters for E. coli are shown in the following table. These values will be used for the modelling.
Parameter description |
Notation |
Value |
Initial bacterial concentration |
b0 |
108 cells/ml |
Initial attractant concentration |
s0 |
0.1 mM or 0.1 mol/m3 |
Bacterial diffusion coefficient |
µ |
1.5*10-5 cm2/s |
Bacterial chemotactic coefficient |
χ |
1.5-75*10-5 cm2/s |
Attractant diffusion coefficient |
D |
10-5 cm2/s |
Reference: Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis II: Bacterial Populations
The assumptions that we have made are as follow:
- The entire root system is assumed to take the shape of a long cylinder. Hence, a cylindrical coordinate system will be used.
- The system is axisymmetric and there is no variation along the vertical length of the root. Hence,

- The system has reached steady state and is time-independent. Hence,

- Degradation of chemoattractant is first order and is described by f = ks where k is the degradation rate of the chemoattractant.
- Bacterial cell growth and death are neglected. Hence, g(b,s) = h(b,s) = 0
Applying the assumptions above, equation (1) becomes
![]()
Rearranging,
![]() -------------------------------------------------(3)
-------------------------------------------------(3)
Equation (3) is in the form of the modified Bessel equation. Hence, the solution of equation (3) is given by,
![]()
Where K0 is the modified Bessel function.
Since it is unrealistic for the concentration to increase to infinity, A=0. And applying the boundary condition, the solution becomes,
![]() -----------------------------------------------------(4)
-----------------------------------------------------(4)
The modeling result show that the steady-state pattern of malate distribution. The concentration of malate is a variable against the distance


Chemotaxis
1. Signal pathway of a single bacterium
- the signal transfer inside the bacterium
chemoattractant stimulation -> chemoreceptor -> CheA -> CheY-P -> flagellar motor -> changed switching frequency between swimming and tumbling (biasing fraction) - the phosphrylation level of CheY can indicate the signal transferring pathway, the CheY-P concentration increases when the chemoreceptor is triggered
- the modeling result will show the optimal concentration to trigger the chemoreceptors (10-6 mol/L)
high = saturated chemoreceptors
low = cannot be detected



2. Bacterial population dynamics
An animation is made to show the movement of the population:
mainly by diffusion, biased motion with the presence of chemoattractant
based on the malate distribution in steady-state and the Spiro model
 "
"