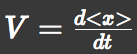Team:UT-Tokyo/Data/Modeling/Model02
From 2011.igem.org
| Line 14: | Line 14: | ||
==Method== | ==Method== | ||
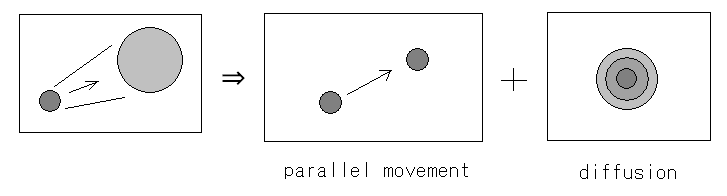
| - | We approximated | + | We approximated the motion of ''E.coli'' groups doing a process of chemotaxis into two factors, that is, parallel translation and diffusion. |
| + | |||
| + | [[File:utt_m2_figure.PNG]] | ||
| + | |||
Let 'V' represent the parallel translation velocity, 'D' represent the diffusion coefficient of ''E.coli'' groups and 'A' represent L-Asp concentration. | Let 'V' represent the parallel translation velocity, 'D' represent the diffusion coefficient of ''E.coli'' groups and 'A' represent L-Asp concentration. | ||
''E.coli'' can detect A and the gradient ∇A. | ''E.coli'' can detect A and the gradient ∇A. | ||
Latest revision as of 02:08, 6 October 2011
Model02

iGEM UT-Tokyo
Modeling/Model2: A simple model for E.coli chemotaxis
Interactive demo
Aim
We tried to derive a simple relationship between Asp concentration and E.coli chemotactic behavior so that it become possible to simulate macroscopic (n~108) E.coli-colony chemotactic behavior in the entire simulation.
Background
SPECS [1] is one of the models simulating E.coli chemotactic behavior, and it considers internal condition of E.coli (receptor methylation etc). It is suitable for semi-macroscopic simulation which has around ten thousand E.coli and the timescale is within a hour. For our system, however, it takes too much time to replicate entire system, because the system includes much more E.coli(about one hundred of million) and the time scale is relatively long (a few days). Therefore we devised a new model based on SPECS which requires less calculation amount.
Method
We approximated the motion of E.coli groups doing a process of chemotaxis into two factors, that is, parallel translation and diffusion.
Let 'V' represent the parallel translation velocity, 'D' represent the diffusion coefficient of E.coli groups and 'A' represent L-Asp concentration. E.coli can detect A and the gradient ∇A. They have an internal circuit to translate these signals into motions of their flagella and try to move towards regions with more Asp. So we thought V and D could be represented as a function of A and ∇A. And then we used the SPECS model to derive these functions.
Here we introduce SPECS briefly. An E.coli belongs to one of two mobile states: "Run" and "Tumble". Run state indicates that E.coli goes straight until the state changes. Tumble state indicates that E.coli is changing its direction and doesn't move around. E.coli changes its state from "Run" to "Tumble" with probability Prt [1/sec]. From "Tumble" to "Run" with Ptr [1/sec]. These probabilities depend on the E.coli internal state. The internal state is represented by two variables: "a" and "m". "a" indicates kinase activity and "m" represents the receptor methylation level of the cell. These vary depending on L-Asp concentration. In addition, SPECS takes into account Brownian fluctuation. Using this model, SPECS tries to replicate the internal circuit of E.coli which translates an Asp concentration distribution into a mobile state.
We processed a Monte Carlo simulation for 20000 E.coli behaving according to SPECS when placed in fields containing different concentrations and gradients of Asp. The shape of the Asp gradient used was exponential according to the following relationship:
where A0 represents the concentration of Asp at x = 0 and x0 a parameter that represents the slope of the gradient.
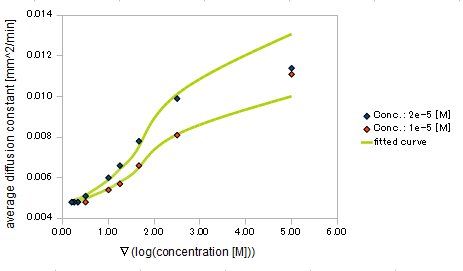
We approximated E.coli movement by a combination of parallel translation and diffusion. We recorded the average position <x> and root-mean-square <x2> over time and then calculated the average velocity:
and the diffusion constant:
We derived the relationship between
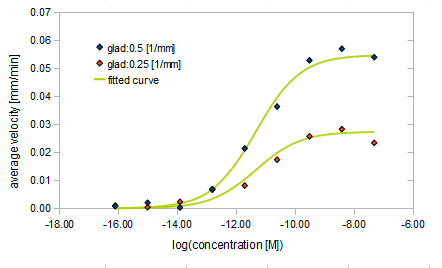
- Asp concentration and average velocity of E.coli
- Asp concentration and diffusion constant of E.coli
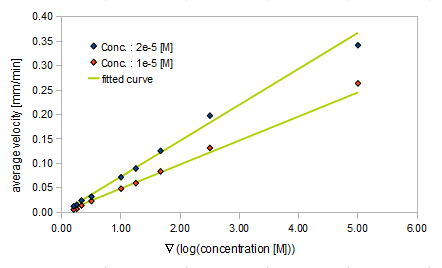
- gradient of Asp concentration and average velocity of E.coli
- gradient of Asp concentration and diffusion constant of E.coli
Finally we fitted approximated curves (represented as functions of A and ∇A) to these data so that we could derive functions we needed in the entire system simulation.
Result
The fitted curves are represented by the following equations.
References
- [1] Jiang L, Ouyang Q, Tu Y (2010) Quantitative Modeling of "Escherichia coli" Chemotactic Motion in Environments Varying in Space and Time. PLoS Comput Biol 6(4): e1000735. doi:10.1371/journal.pcbi.1000735
 "
"