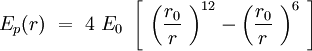Team:Paris Bettencourt/Modeling/Assisted diffusion/Membrane tension
From 2011.igem.org
| (54 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
__NOTOC__ | __NOTOC__ | ||
<html> | <html> | ||
| - | <h1> | + | <h1>2. Membrane tension calculation</h1> |
| - | + | ||
| + | <p> | ||
| + | Once the nanotube connexion between two bacteria is established ( click <a href='https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion/Tube_formation'>here</a> to see the details on the nanotube formation ) what happens? Let's look on the membrane tension of two bacteria. | ||
| + | </p> | ||
| - | + | <h2>Motivation</h2> | |
| - | + | <p> | |
| + | Let's evaluate the constraints that impact the membrane. As it is a Gram positive bacteria, the external sugar envelope imposes the shape of the bacteria. On the other hand, the osmotic pressure is pushing the membrane against the sugar wall. We assume that on the time scale of our model, the total number of phospholipids inside the membrane is fixed, but the density of phospholipids can fluctuate depending on the phospholipid production. So we can pretend that our system is evolving through a series of quasi-equilibrium states. | ||
| + | </p> | ||
<html> | <html> | ||
| - | |||
<table> | <table> | ||
<tr> | <tr> | ||
| - | <td align="center"><img src="https://static.igem.org/mediawiki/2011/e/e9/Image_phospholipide.png" height=200px></td> | + | <td><center><img src="https://static.igem.org/mediawiki/2011/8/8a/MembraneCompression.png" height=200px></center></td> |
| - | <td align="center"><img src="https://static.igem.org/mediawiki/2011/8/82/Mod%C3%A8le_Phospholipide.png" height=200px></td> | + | <td><center><img src="https://static.igem.org/mediawiki/2011/d/d3/MembraneExtension.png" height=250px></center></td> |
| + | <tr> | ||
| + | <tr> | ||
| + | <td><p><center><u><b>Fig. 2:</b></u> If there is an excess of phospholipids, the membrane is being compressed<p></td> | ||
| + | <td><p><center><u><b>Fig. 3:</b></u> If there are not enough phospholipids, the membrane is being extended<p></td> | ||
| + | <tr> | ||
| + | </table> | ||
| + | </html> | ||
| + | |||
| + | <p> | ||
| + | The membrane tension is caused by interaction between phospholipids on the surface of bacteria. Closer the phospholipids are to each other, more the membrane is tense. | ||
| + | </p> | ||
| + | |||
| + | <p> | ||
| + | Can we describe the interaction between two phospholipids in the membrane? The question is complicated, but we will demonstrate that by describing properly the phospholipid, as it is reasonable to fit a Lennard-Jones potential energy to this interaction. Since the speed of conformational equilibration of phospholipid is way faster than the sliding of neighboring phospholipids we can consider phospholipids as cylinders (see the Fig. 4). To make things even simpler we decided to approximate these cylinders as points(see the Fig. 5). | ||
| + | </p> | ||
| + | |||
| + | <html> | ||
| + | <br/> | ||
| + | <center><table> | ||
| + | <tr> | ||
| + | <td align="center" style="width:400px"><img src="https://static.igem.org/mediawiki/2011/e/e9/Image_phospholipide.png" height=200px></td> | ||
| + | <td align="center" style="width:400px"><img src="https://static.igem.org/mediawiki/2011/8/82/Mod%C3%A8le_Phospholipide.png" height=200px></td> | ||
| + | <td align="center" style="width:400px"><img src="https://static.igem.org/mediawiki/2011/1/13/Point_ParisBettencourt.png" height=200px></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td align="center"><center>< | + | <td align="center"><center><u><b>Fig. 3:</b></u> Chemical structure of a phospholipid</center></td> |
| - | <td align="center"><center><b><u> | + | <td align="center"><center><u><b>Fig. 4:</b></u> Cylindrical approximation of Israelachvili for a phospholipid</center></td> |
| + | <td align="center"><center><u><b>Fig. 5:</b></u> Our approximation</center></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| + | </center> | ||
<br/> | <br/> | ||
</html> | </html> | ||
| + | <center><h3> | ||
| + | As we can see the modelers go always straight to the point :) | ||
| + | </h3></center> | ||
| + | |||
| + | <p> | ||
Speaking in terms of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a steric repulsion keeps the molecules apart, and the hydrophobic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients. | Speaking in terms of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a steric repulsion keeps the molecules apart, and the hydrophobic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients. | ||
| + | </p> | ||
[[File:LJpot.jpg|center|Lennard-Jones potential]] | [[File:LJpot.jpg|center|Lennard-Jones potential]] | ||
| Line 31: | Line 65: | ||
== The membrane tension calculation == | == The membrane tension calculation == | ||
<html> | <html> | ||
| + | |||
| + | <div style="margin-left:50px; margin-right:50px; padding: 5px; border:2px solid black;"><b><p>Some hypotheses used : | ||
| + | <ul> | ||
| + | <li>We deal with a system under fixed temperature, so we can reason in canonical ensemble terminology</li> | ||
| + | <li>Every bacterium in this model has a perfectly spherical form, so each phospholipid on it has 4 degrees of freedom (2 coordinates, 2 momentums per phospholipid)</li> | ||
| + | <li>We will consider phosphlipids equally distributed on the membrane and only the initial density of this distribution can change</li> | ||
| + | </ul></p></b></div> | ||
Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the whole sphere surface per one phospholipid : | Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the whole sphere surface per one phospholipid : | ||
| Line 36: | Line 77: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/f/fa/Surface_per_phospholipid.png'> | + | <img src='https://static.igem.org/mediawiki/2011/f/fa/Surface_per_phospholipid.png' style="height:40px"> |
</center> | </center> | ||
</p> | </p> | ||
| Line 44: | Line 85: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/c/c6/Characteristical_length_between_2_phl.png'> | + | <img src='https://static.igem.org/mediawiki/2011/c/c6/Characteristical_length_between_2_phl.png' style="height:35px"> |
</center> | </center> | ||
</p> | </p> | ||
| Line 56: | Line 97: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/2/27/Partition_function.png'> | + | <img src='https://static.igem.org/mediawiki/2011/2/27/Partition_function.png' style="height:35px"> |
</center> | </center> | ||
| + | </p> | ||
| + | |||
| + | <p> | ||
| + | Using statistical physics approach, we can say that the phase space has 4N dimensions: two dimensions of impulsion and two dimensions of coordinate for each particle (N is the number of particles in the system). | ||
</p> | </p> | ||
| Line 64: | Line 109: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/b/be/Hamiltonian.png' style='width: | + | <img src='https://static.igem.org/mediawiki/2011/b/be/Hamiltonian.png' style='width:90%;'> |
</center> | </center> | ||
</p> | </p> | ||
| Line 72: | Line 117: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/c/cf/Free_energy.png'> | + | <img src='https://static.igem.org/mediawiki/2011/c/cf/Free_energy.png' style="height:30px"> |
</center> | </center> | ||
</p> | </p> | ||
| Line 80: | Line 125: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/4/49/Free_energy_total.png' style='width: | + | <img src='https://static.igem.org/mediawiki/2011/4/49/Free_energy_total.png' style='width:80%;'> |
</center> | </center> | ||
</p> | </p> | ||
| Line 86: | Line 131: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/f/f4/Tension.png'> | + | <img src='https://static.igem.org/mediawiki/2011/f/f4/Tension.png' style="height:50px"> |
</center> | </center> | ||
</p> | </p> | ||
| Line 94: | Line 139: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/f/f2/Tension_1.png'> | + | <img src='https://static.igem.org/mediawiki/2011/f/f2/Tension_1.png' style="height:60px"> |
</center> | </center> | ||
</p> | </p> | ||
| Line 102: | Line 147: | ||
<p> | <p> | ||
<center> | <center> | ||
| - | <img src='https://static.igem.org/mediawiki/2011/8/87/Tension_2.png'> | + | <img src='https://static.igem.org/mediawiki/2011/8/87/Tension_2.png' style="height:55px"> |
</center> | </center> | ||
</p> | </p> | ||
| + | |||
| + | <p> | ||
| + | The next step after the membrane tension calculation is the <a href='https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion/From_membrane_tension_to_liquid_flux'>3. Pressure difference and Result section.</a> | ||
| + | </p> | ||
| + | |||
| + | <html> | ||
| + | <p> | ||
| + | Click here to come back to <a href='https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion'>Assisted diffusion section.</a></p> | ||
| + | </html> | ||
| + | |||
| + | |||
| + | <html> | ||
| + | <!-- PAGE FOOTER -- ITEMS FROM COLUMN ! HAVE BEEN MOVED HERE -- RDR --> | ||
| + | |||
| + | <div id="footer-wrapper"> | ||
| + | <div id="footer"> | ||
| + | <div id="f-poweredbyico"><a href="http://www.mediawiki.org/"><img src="/wiki/skins/common/images/poweredby_mediawiki_88x31.png" height="31" width="88" alt="Powered by MediaWiki" /></a></div> <div id="f-copyrightico"><a href="http://creativecommons.org/licenses/by/3.0/"><img src="http://i.creativecommons.org/l/by/3.0/88x31.png" alt="Attribution 3.0 Unported" width="88" height="31" /></a></div> <ul id="f-list"> | ||
| + | |||
| + | |||
| + | <!-- Recentchanges is not handles well DEBUG --> | ||
| + | <li id="t-recentchanges"><a href="/Special:RecentChanges" | ||
| + | title='Recent changes'>Recent changes</a></li> | ||
| + | |||
| + | <li id="t-whatlinkshere"><a href="/Special:WhatLinksHere/Team:Paris_Bettencourt/Modeling" | ||
| + | title="List of all wiki pages that link here [j]" accesskey="j">What links here</a></li> | ||
| + | |||
| + | <li id="t-recentchangeslinked"><a href="/Special:RecentChangesLinked/Team:Paris_Bettencourt/Modeling" | ||
| + | title="Recent changes in pages linked from this page [k]" accesskey="k">Related changes</a></li> | ||
| + | |||
| + | |||
| + | |||
| + | <li id="t-upload"><a href="/Special:Upload" | ||
| + | title="Upload files [u]" accesskey="u">Upload file</a> | ||
| + | </li> | ||
| + | <li id="t-specialpages"><a href="/Special:SpecialPages" | ||
| + | title="List of all special pages [q]" accesskey="q">Special pages</a> | ||
| + | |||
| + | </li> | ||
| + | <li><a href='/Special:Preferences'>My preferences</a></li> | ||
| + | </ul> | ||
| + | </div> <!-- close footer --> | ||
| + | <div id='footer'> | ||
| + | <ul id="f-list"> | ||
| + | |||
| + | <li id="t-print"><a href="/wiki/index.php?title=Team:Paris_Bettencourt/Modeling&printable=yes" | ||
| + | title="Printable version of this page [p]" accesskey="p">Printable version</a> | ||
| + | |||
| + | </li> | ||
| + | |||
| + | <li id="t-permalink"><a href="/wiki/index.php?title=Team:Paris_Bettencourt/Modeling&oldid=86565" | ||
| + | title="Permanent link to this revision of the page">Permanent link</a> | ||
| + | </li> | ||
| + | |||
| + | |||
| + | <li id="privacy"><a href="/2011.igem.org:Privacy_policy" title="2011.igem.org:Privacy policy">Privacy policy</a></li> | ||
| + | <li id="disclaimer"><a href="/2011.igem.org:General_disclaimer" title="2011.igem.org:General disclaimer">Disclaimers</a></li> | ||
| + | </ul> | ||
| + | |||
| + | </div> <!-- close footer --> | ||
| + | </div> <!-- close footer-wrapper --> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | </html> | ||
| + | <html> | ||
| + | <div id="scroll_left"><a href="https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion"><img src="https://static.igem.org/mediawiki/2011/0/0a/Arrow-left-big.png" style="width:100%;"></a><a href="https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion">To come back to Assisted diffusion section</a></div> | ||
| + | <div id="scroll_right"><a href="https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion/From_membrane_tension_to_liquid_flux"><img src="https://static.igem.org/mediawiki/2011/e/e0/Arrow-right-big.png" style="width:100%;"></a><a href="https://2011.igem.org/Team:Paris_Bettencourt/Modeling/Assisted_diffusion/From_membrane_tension_to_liquid_flux">To go to Pressure difference and Result section</a></div> | ||
</html> | </html> | ||
Latest revision as of 03:06, 29 October 2011

2. Membrane tension calculation
Once the nanotube connexion between two bacteria is established ( click here to see the details on the nanotube formation ) what happens? Let's look on the membrane tension of two bacteria.
Motivation
Let's evaluate the constraints that impact the membrane. As it is a Gram positive bacteria, the external sugar envelope imposes the shape of the bacteria. On the other hand, the osmotic pressure is pushing the membrane against the sugar wall. We assume that on the time scale of our model, the total number of phospholipids inside the membrane is fixed, but the density of phospholipids can fluctuate depending on the phospholipid production. So we can pretend that our system is evolving through a series of quasi-equilibrium states.
 |
 |
The membrane tension is caused by interaction between phospholipids on the surface of bacteria. Closer the phospholipids are to each other, more the membrane is tense.
Can we describe the interaction between two phospholipids in the membrane? The question is complicated, but we will demonstrate that by describing properly the phospholipid, as it is reasonable to fit a Lennard-Jones potential energy to this interaction. Since the speed of conformational equilibration of phospholipid is way faster than the sliding of neighboring phospholipids we can consider phospholipids as cylinders (see the Fig. 4). To make things even simpler we decided to approximate these cylinders as points(see the Fig. 5).
 |
 |
 |
As we can see the modelers go always straight to the point :)
Speaking in terms of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a steric repulsion keeps the molecules apart, and the hydrophobic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients.
The membrane tension calculation
Some hypotheses used :
- We deal with a system under fixed temperature, so we can reason in canonical ensemble terminology
- Every bacterium in this model has a perfectly spherical form, so each phospholipid on it has 4 degrees of freedom (2 coordinates, 2 momentums per phospholipid)
- We will consider phosphlipids equally distributed on the membrane and only the initial density of this distribution can change



Using statistical physics approach, we can say that the phase space has 4N dimensions: two dimensions of impulsion and two dimensions of coordinate for each particle (N is the number of particles in the system).
where the Hamiltonian is :






The next step after the membrane tension calculation is the 3. Pressure difference and Result section.
Click here to come back to Assisted diffusion section.
 "
"