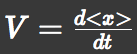Team:UT-Tokyo/Data/Modeling/Model02

From 2011.igem.org

(Difference between revisions)
 
(14 intermediate revisions not shown)
Line 1: Line 1:
-
{{:Team:UT-Tokyo/Templates/BeginContent|fullpagename=Team:UT-Tokyo/Data/Modeling/Model02|subpagename=Model2}}
+
{{:Team:UT-Tokyo/Templates/BeginContent|fullpagename=Team:UT-Tokyo/Data/Modeling/Model02|subpagename=Model02}}
-
=A simple model for E.coli chemotaxis=
+
=[[Team:UT-Tokyo/Data/Modeling|Modeling]]/Model2: A simple model for ''E.coli'' chemotaxis=
-
=Aim=
+
=[[Team:UT-Tokyo/Data/Modeling/Model02/applet|Interactive demo]]=
-
We derived a simple relationship between Asp concentration and E.coli chemotaxis so that
+
-
we were able to simulate macroscopic (n~10<html><sup>8</sup></html>) E.coli colony chemotacitc behavior in the entire simulation.
+
-
=Background=
+
==Aim==
-
SPECS <html><sup class="ref">[1]</sup></html> is one of the model simulating E.coli's chemotactic behavior.
+
We tried to derive a simple relationship between Asp concentration and ''E.coli'' chemotactic behavior so that
-
It considers internal condition of E.coli (receptor methylation etc) so it is a relatively strict taxis model.  It is suitable for semi-macroscopic simulation which has around ten thousand E.coli and the timescale is within a hour.
+
it become possible to simulate macroscopic (n~10<html><sup>8</sup></html>) ''E.coli''-colony chemotactic behavior in the entire simulation.
-
For our system, however, it takes too much time to replicate entire system, because the system includes much more E.coli(about one hundred of million) and the time scale is relatively long (a few days).
+
 
 +
==Background==
 +
SPECS <html><sup class="ref">[1]</sup></html> is one of the models simulating ''E.coli'' chemotactic behavior, and it considers internal condition of ''E.coli'' (receptor methylation etc).  It is suitable for semi-macroscopic simulation which has around ten thousand ''E.coli'' and the timescale is within a hour.
 +
For our system, however, it takes too much time to replicate entire system, because the system includes much more ''E.coli''(about one hundred of million) and the time scale is relatively long (a few days).
Therefore we devised a new model based on SPECS which requires less calculation amount.
Therefore we devised a new model based on SPECS which requires less calculation amount.
-
=Method=
+
==Method==
-
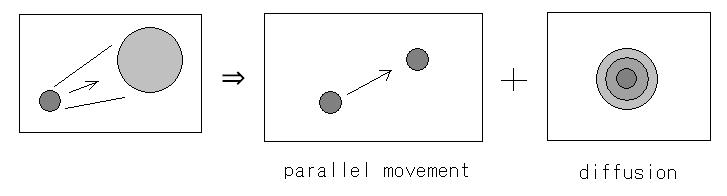
We approximated chemotactic motion of E.coli groups into two factors, that is, parallel translation and diffusion.
+
We approximated the motion of ''E.coli'' groups doing a process of chemotaxis into two factors, that is, parallel translation and diffusion.
-
Let 'V' represents a parallel translation velocity 'D' represents a diffusion coefficient of E.coli groups and 'A' represents L-Asp concentration.
+
 
-
E.coli can detect A and its gradient ∇A.
+
[[File:utt_m2_figure.PNG]]
-
They have an internal circuit to translate these signal into motions of their flagellum and try to run toward Asp-richer region.
+
 
-
So we thought V and D could be represented as a functions of A and ∇A.
+
Let 'V' represent the parallel translation velocity, 'D' represent the diffusion coefficient of ''E.coli'' groups and 'A' represent L-Asp concentration.
-
And then we used SPECS model to derive these functions.
+
''E.coli'' can detect A and the gradient ∇A.
 +
They have an internal circuit to translate these signals into motions of their flagella and try to move towards regions with more Asp.
 +
So we thought V and D could be represented as a function of A and ∇A.
 +
And then we used the SPECS model to derive these functions.
Here we introduce SPECS briefly.
Here we introduce SPECS briefly.
-
An E.coli belongs to one of two mobile states: "Run" and "Tumble".
+
An ''E.coli'' belongs to one of two mobile states: "Run" and "Tumble".
-
Run state indicates that E.coli goes straight until the state changes.
+
Run state indicates that ''E.coli'' goes straight until the state changes.
-
Tumble state indicates that E.coli is changing its direction and doesn't move around.
+
Tumble state indicates that ''E.coli'' is changing its direction and doesn't move around.
-
E.coli changes its state "Run" to "Tumble" with probability P<html><sub>rt</sub></html> [1/sec].
+
''E.coli'' changes its state from "Run" to "Tumble" with probability P<html><sub>rt</sub> </html> [1/sec].
-
"Tumble" to "Run" with P<html><sub>tr</sub></html> [1/sec].
+
From "Tumble" to "Run" with P<html><sub>tr</sub></html> [1/sec].
-
These probability depend on the E.coli's internal state.
+
These probabilities depend on the ''E.coli'' internal state.
-
The internal state is represented as two variables: "a" and "m".
+
The internal state is represented by two variables: "a" and "m".
-
"a" indicates its kinase activity and "m" represents its receptor's methylation level.
+
"a" indicates kinase activity and "m" represents the receptor methylation level of the cell.
-
They vary depending on L-Asp concentration.
+
These vary depending on L-Asp concentration.
-
In addition, SPECS concern the Brownian fluctuation.
+
In addition, SPECS takes into account Brownian fluctuation.
-
From these modeling, SPECS can replicate the internal circuit of E.coli which translates Asp concentration distribution into its mobile state.
+
Using this model, SPECS tries to replicate the internal circuit of ''E.coli'' which translates an Asp concentration distribution into a mobile state.
-
We processed Monte Carlo simulation for 20000 E.coli which behavior was based on SPECS in some different Asp concentration and its gradient strength.  The shape of the Asp gradient we used were exponential.
+
We processed a Monte Carlo simulation for 20000 ''E.coli'' behaving according to SPECS when placed in fields containing different concentrations and gradients of Asp.  The shape of the Asp gradient used was exponential according to the following relationship:
[[File:utt_m2_eqn1.png]]
[[File:utt_m2_eqn1.png]]
-
We approximated E.coli movement as the combination of parallel translation and diffusion.
+
where A0 represents the concentration of Asp at x = 0 and x0 a parameter that represents the slope of the gradient.
-
We recorded the time course of average position <x> and root-mean-square ¥<x^2> and then
+
 
-
calculated average velocity  
+
We approximated ''E.coli'' movement by a combination of parallel translation and diffusion.
 +
We recorded the average position <x> and root-mean-square <x<html><sup>2</sup></html>> over time and then
 +
calculated the average velocity:
[[File:utt_m2_eqn2.png]]
[[File:utt_m2_eqn2.png]]
-
and the diffusion constant.
+
and the diffusion constant:
[[File:utt_m2_eqn3.png]]
[[File:utt_m2_eqn3.png]]
We derived the relationship between
We derived the relationship between
-
* Asp concentration and average velocity of E.coli
+
* Asp concentration and average velocity of ''E.coli''
-
* Asp concentration and diffusion constant of E.coli
+
* Asp concentration and diffusion constant of ''E.coli''
-
* gradient of Asp concentration and average velocity of E.coli
+
* gradient of Asp concentration and average velocity of ''E.coli''
-
* gradient of Asp concentration and diffusion constant of E.coli
+
* gradient of Asp concentration and diffusion constant of ''E.coli''
-
Finally we fitted approximated curve (represented as functions of A and ∇A) to these data so that we could use these functions in the entire simulation.
+
Finally we fitted approximated curves (represented as functions of A and ∇A) to these data so that we could derive functions we needed in the entire system simulation.
-
=Result=
+
==Result==
-
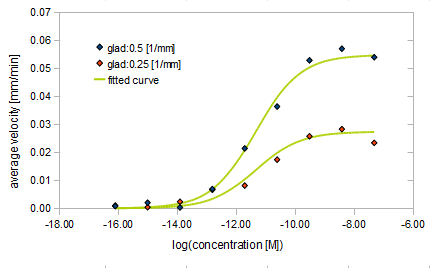
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig1.png|caption=Figure 1. relationship between Asp conc. and avg. velocity}
+
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig1.png|caption=Figure 1. relationship between Asp conc. and avg. velocity}}
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig2.png|caption=Figure 2. relationship between gradient of Asp conc. and avg. velocity}}
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig2.png|caption=Figure 2. relationship between gradient of Asp conc. and avg. velocity}}
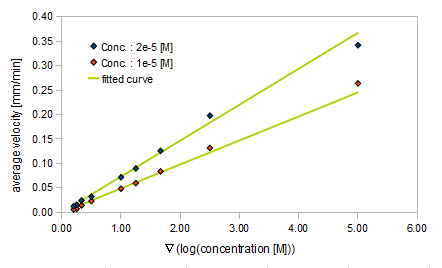
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig3.png|caption=Figure 3. relationship between Asp conc. and diffusion coef}}
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig3.png|caption=Figure 3. relationship between Asp conc. and diffusion coef}}
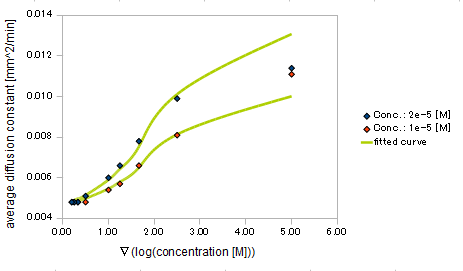
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig4.png|caption=Figure 4. relationship between gradient of Asp conc. and diffusion coef}}
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig4.png|caption=Figure 4. relationship between gradient of Asp conc. and diffusion coef}}
-
The fitted curves are represented by following equation.
+
The fitted curves are represented by the following equations.
[[File:utt_m2_eqn4.png]]
[[File:utt_m2_eqn4.png]]
Line 71: Line 77:
<div id="references">
<div id="references">
<ul>
<ul>
-
   <li id="ref_1">[1] Jiang L, Ouyang Q, Tu Y (2010) Quantitative Modeling of Escherichia coli Chemotactic Motion in Environments Varying in Space and Time. PLoS Comput Biol 6(4): e1000735. doi:10.1371/journal.pcbi.1000735</li>
+
   <li id="ref_1">[1] Jiang L, Ouyang Q, Tu Y (2010) Quantitative Modeling of "Escherichia coli" Chemotactic Motion in Environments Varying in Space and Time. PLoS Comput Biol 6(4): e1000735. doi:10.1371/journal.pcbi.1000735</li>
</ul>
</ul>
</div>
</div>
</html>
</html>
{{:Team:UT-Tokyo/Templates/EndContent}}
{{:Team:UT-Tokyo/Templates/EndContent}}

Latest revision as of 02:08, 6 October 2011

Modeling/Model2: A simple model for E.coli chemotaxis

Interactive demo

Aim

We tried to derive a simple relationship between Asp concentration and E.coli chemotactic behavior so that it become possible to simulate macroscopic (n~108) E.coli-colony chemotactic behavior in the entire simulation.

Background

SPECS [1] is one of the models simulating E.coli chemotactic behavior, and it considers internal condition of E.coli (receptor methylation etc). It is suitable for semi-macroscopic simulation which has around ten thousand E.coli and the timescale is within a hour. For our system, however, it takes too much time to replicate entire system, because the system includes much more E.coli(about one hundred of million) and the time scale is relatively long (a few days). Therefore we devised a new model based on SPECS which requires less calculation amount.

Method

We approximated the motion of E.coli groups doing a process of chemotaxis into two factors, that is, parallel translation and diffusion.

Utt m2 figure.PNG

Let 'V' represent the parallel translation velocity, 'D' represent the diffusion coefficient of E.coli groups and 'A' represent L-Asp concentration. E.coli can detect A and the gradient ∇A. They have an internal circuit to translate these signals into motions of their flagella and try to move towards regions with more Asp. So we thought V and D could be represented as a function of A and ∇A. And then we used the SPECS model to derive these functions.

Here we introduce SPECS briefly. An E.coli belongs to one of two mobile states: "Run" and "Tumble". Run state indicates that E.coli goes straight until the state changes. Tumble state indicates that E.coli is changing its direction and doesn't move around. E.coli changes its state from "Run" to "Tumble" with probability Prt [1/sec]. From "Tumble" to "Run" with Ptr [1/sec]. These probabilities depend on the E.coli internal state. The internal state is represented by two variables: "a" and "m". "a" indicates kinase activity and "m" represents the receptor methylation level of the cell. These vary depending on L-Asp concentration. In addition, SPECS takes into account Brownian fluctuation. Using this model, SPECS tries to replicate the internal circuit of E.coli which translates an Asp concentration distribution into a mobile state.

We processed a Monte Carlo simulation for 20000 E.coli behaving according to SPECS when placed in fields containing different concentrations and gradients of Asp. The shape of the Asp gradient used was exponential according to the following relationship:

Utt m2 eqn1.png

where A0 represents the concentration of Asp at x = 0 and x0 a parameter that represents the slope of the gradient.

We approximated E.coli movement by a combination of parallel translation and diffusion. We recorded the average position <x> and root-mean-square <x2> over time and then calculated the average velocity:

Utt m2 eqn2.png

and the diffusion constant:

Utt m2 eqn3.png

We derived the relationship between

  • Asp concentration and average velocity of E.coli
  • Asp concentration and diffusion constant of E.coli
  • gradient of Asp concentration and average velocity of E.coli
  • gradient of Asp concentration and diffusion constant of E.coli

Finally we fitted approximated curves (represented as functions of A and ∇A) to these data so that we could derive functions we needed in the entire system simulation.

Result

Figure 1. relationship between Asp conc. and avg. velocity
Figure 1. relationship between Asp conc. and avg. velocity

Figure 2. relationship between gradient of Asp conc. and avg. velocity
Figure 2. relationship between gradient of Asp conc. and avg. velocity

Figure 3. relationship between Asp conc. and diffusion coef
Figure 3. relationship between Asp conc. and diffusion coef

Figure 4. relationship between gradient of Asp conc. and diffusion coef
Figure 4. relationship between gradient of Asp conc. and diffusion coef

The fitted curves are represented by the following equations.

Utt m2 eqn4.png

Utt m2 eqn5.png

References

  • [1] Jiang L, Ouyang Q, Tu Y (2010) Quantitative Modeling of "Escherichia coli" Chemotactic Motion in Environments Varying in Space and Time. PLoS Comput Biol 6(4): e1000735. doi:10.1371/journal.pcbi.1000735

Retrieved from "http://2011.igem.org/Team:UT-Tokyo/Data/Modeling/Model02"