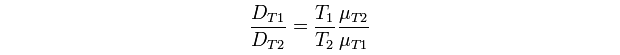Team:Edinburgh/Model Comparison
From 2011.igem.org
(→Ability to reach steady state) |
|||
| (43 intermediate revisions not shown) | |||
| Line 7: | Line 7: | ||
<p class="h1">Model Comparison</p> | <p class="h1">Model Comparison</p> | ||
| - | + | ==The approaches == | |
| - | *'''MATLAB''' - Within the reactor tasked with degrading cellulose into glucose in the biorefinery, temperature, enzyme concentration, substrate reactivity as well as xylose, cellobiose and glucose inhibition all govern the amount of glucose product. Deterministic modelling using a set of ordinary differential equations highlights the essential kinetic relationship among the enzymes, exo/endo-glucanase and β-glucosidase. By solving these governing equations using the numerical tool MATLAB the level of degradation is qualitatively predicted | + | *'''MATLAB''' - Within the reactor tasked with degrading cellulose into glucose in the biorefinery, temperature, enzyme concentration, substrate reactivity as well as xylose, cellobiose and glucose inhibition all govern the amount of glucose product. Deterministic modelling using a set of <span class="hardword" id="ode">ordinary differential equations</span> highlights the essential kinetic relationship among the enzymes, exo/endo-glucanase and β-glucosidase. By solving these governing equations using the numerical tool MATLAB the level of degradation of cellulose is qualitatively predicted. |
| - | + | ||
| - | + | ||
*'''Kappa''' - As an alternative, <span class="hardword" id="stochastic">stochastic</span> models were created using the Kappa language. The system is defined in terms of many discrete agents and rules of their interaction. The Kappa simulator then uses probabilistic equations to simulate the evolution of the system, incorporating an indeterministic element into the system. | *'''Kappa''' - As an alternative, <span class="hardword" id="stochastic">stochastic</span> models were created using the Kappa language. The system is defined in terms of many discrete agents and rules of their interaction. The Kappa simulator then uses probabilistic equations to simulate the evolution of the system, incorporating an indeterministic element into the system. | ||
| - | *'''Spatial | + | *'''Spatial Kappa''' - Because of problems with the Kappa language, we decided to use a spatial extension developed by the [https://2010.igem.org/Team:Edinburgh Edinburgh 2010] iGEM team. This adds extra functionality to the language by introducing the concept of '''space'''. |
| - | == | + | *'''C model''' - Intended more as a demonstration of synergy than an accurate model of the world, the cellulose is represented using a simple two-dimensional grid, on which enzymes move using <span class="hardword" id="brownian">Brownian motion</span>. This is an ''ad hoc'' model made in a general programming language. It was inspired by cellular-automata systems, though cannot really be considered one. |
| - | We | + | ==Comparison criteria== |
| - | + | We chose the following criteria which are desirable in a model. They also show the main differences and similarities among our models, however the list is non-exhaustive. | |
| - | + | ||
=== Flexibility === | === Flexibility === | ||
| - | We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, | + | We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme. |
| - | *Temperature | + | *'''Temperature''' |
| - | **MATLAB - Very | + | ** MATLAB - Very flexible as it incorporates the Arrhenius law which models the temperature-dependent reaction rate constant. You can input a temperature into an interactive prompt. |
| - | **Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that using the Stokes-Einstein equation:<br/> | + | ** Spatial Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:<br/>[[File:Edinburgh-Stokes-Einstein.png|thumb|center|620px|T<sub>1</sub> and T<sub>2</sub> denote temperatures 1 and 2, respectively<br /> |
| - | **C - | + | D is the diffusion coefficient (cm<sup>2</sup>/s)<br /> |
| - | + | T is the absolute temperature (°K),<br /> | |
| + | μ is the dynamic viscosity of the solvent (Pa·s)<br /><br /> | ||
| + | (After [http://en.wikipedia.org/wiki/Mass_diffusivity#Temperature_dependence_of_the_diffusion_coefficient Wikipedia])]] | ||
| + | ** C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds. | ||
| + | |||
| + | *'''Enzyme concentration''' | ||
| + | ** MATLAB - Can easily be changed by inputting a value (in the range of 0-1 g/kg for each enzyme) into an interactive prompt. The flexibility is beneficial especially when investigating optimum operating conditions in the biorefinery. | ||
| + | ** Kappa and Spatial Kappa - It is possible to change the number of enzyme agents by editing a separate file, which affects the ''relative'' concentration of enzymes (say, 3 times more of enzyme A than B). However, it would be non-trivial to translate that into an ''absolute'' value (e.g. 0.5 g of enzyme per 1kg of solution). | ||
| + | ** C - Similarly to Kappa, this can easily be changed in relative terms. | ||
| + | |||
| + | *'''Strength of inhibition''' | ||
| + | ** MATLAB - Incorporates inhibition of enzymes based on glucose and cellobiose concentrations; the strength can be changed. There is also scope for xylose inhibition, but it is set to zero in this model. | ||
| + | ** Kappa and Spatial Kappa - The inhibition rates can be easily changed by editing a file with parameters. | ||
| + | ** C - Incorporates inhibition of exoglucanase by individual cellobiose molecules based on spatial location. Could be extended to include inhibition by glucose; and also to have free glucose taken out of the system after it is made. | ||
| + | |||
| + | *'''Amount of raw material input''' | ||
| + | ** MATLAB - An interactive prompt asks the user for an initial amount of cellulose. | ||
| + | ** Kappa and Spatial Kappa - The initial amount of cellulose can be modified by editing a file. Also, in Spatial Kappa [[Team:Edinburgh/Cellulases_(Kappa_model)#Additional_cellulose | we ran experiments]] with adding more cellulose during the process. | ||
| + | ** C - The amount can be passed as a command-line argument. | ||
=== Computational cost === | === Computational cost === | ||
| + | |||
| + | The MATLAB, C and Kappa models do their work in relatively short periods of time. | ||
| + | |||
| + | In contrast, the Spatial Kappa model takes a significant amount of time to run (about 30 minutes, depending on the settings of parameters). This is because when rules are translated from Spatial Kappa to the simulator, the complexity of the system increases. For a system with ''n'' compartments in ''d'' dimensions, one rule would need to be translated into ''n × d'' rules, to take into account possible spatial locations of agents. That increases the time taken to run a simulation by a factor of ''n × d''. Fortunately, we had access to a computing cluster (ECDF, [http://www.ecdf.ed.ac.uk/ www.ecdf.ed.ac.uk]), where we could run 1,000 simulations in about 5 hours. | ||
=== Representing reality === | === Representing reality === | ||
| + | The MATLAB model is based on the <span class="hardword" id="empirical">empirical</span> literature, and so should be the best representation of reality. Units of substrate is grams per kilogram (g/kg) and time is in hours. The kinetic rates are based on experimental data which gives the model some validity, however only within certain time limits. | ||
| + | |||
| + | However, since literature was not available for the synergistic system (with closely linked enzymes) we are considering, we had nothing to base a MATLAB model of synergy on. So, our only MATLAB model is the non-synergistic system. | ||
| + | |||
| + | The C and Spatial Kappa models were capable of comparing a synergistic and a non-synergistic system, but in both cases the model is highly abstract and based only on our understanding of the system due to unavailability of empirical data for dynamics of cellulose, cellobiose and glucose. | ||
| + | |||
| + | == Conclusions == | ||
| + | Although it is hard to compare the different approaches we took and even harder to choose and recommend the best one, our modelling gave us some important insights. | ||
| + | |||
| + | To begin with, we successfully modelled synergy in C and Spatial Kappa, so these models tell us that '''synergy is a viable option'''. In case of MATLAB, there is still potential to improve the model to show synergy (by adding more ODEs), whereas it would be at least very cumbersome to do the same in plain Kappa. | ||
| + | |||
| + | The '''MATLAB model should be the one most closely representing the real-world system'''. That is due to the fact that the model is built using experimentally adjusted values of constants and informed with known reaction equations. However, given sufficient data, it is '''also possible to adjust the Kappa / Spatial Kappa models''' to use different kinetic rates and concentrations of enzymes. It would require major modifications to achieve the same in the C model. | ||
| + | |||
| + | The stochastic route taken by the C and (Spatial) Kappa models means that '''multiple simulations''' need to be run and averaged in order to get a robust estimate of cellulose dynamics. Whereas this takes a relatively short time for the '''C and Kappa models''', '''Spatial Kappa''' considerably increases the amount of time needed to do that. | ||
| + | |||
| + | We would say that, as a general conclusion, '''all of our approaches have their strong points''' and are suited to different tasks - the stochastic approaches show us '''how''' our system works, whereas the deterministic approach gives us some '''real numbers''' against which to test the system. | ||
</div> <!-- /main_body--> | </div> <!-- /main_body--> | ||
<html></div> <!-- /mids --></html> | <html></div> <!-- /mids --></html> | ||
Latest revision as of 20:02, 28 October 2011
Model Comparison
Contents[hide] |
The approaches
- MATLAB - Within the reactor tasked with degrading cellulose into glucose in the biorefinery, temperature, enzyme concentration, substrate reactivity as well as xylose, cellobiose and glucose inhibition all govern the amount of glucose product. Deterministic modelling using a set of ordinary differential equations highlights the essential kinetic relationship among the enzymes, exo/endo-glucanase and β-glucosidase. By solving these governing equations using the numerical tool MATLAB the level of degradation of cellulose is qualitatively predicted.
- Kappa - As an alternative, stochastic models were created using the Kappa language. The system is defined in terms of many discrete agents and rules of their interaction. The Kappa simulator then uses probabilistic equations to simulate the evolution of the system, incorporating an indeterministic element into the system.
- Spatial Kappa - Because of problems with the Kappa language, we decided to use a spatial extension developed by the Edinburgh 2010 iGEM team. This adds extra functionality to the language by introducing the concept of space.
- C model - Intended more as a demonstration of synergy than an accurate model of the world, the cellulose is represented using a simple two-dimensional grid, on which enzymes move using Brownian motion. This is an ad hoc model made in a general programming language. It was inspired by cellular-automata systems, though cannot really be considered one.
Comparison criteria
We chose the following criteria which are desirable in a model. They also show the main differences and similarities among our models, however the list is non-exhaustive.
Flexibility
We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme.
- Temperature
- MATLAB - Very flexible as it incorporates the Arrhenius law which models the temperature-dependent reaction rate constant. You can input a temperature into an interactive prompt.
- Spatial Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:
- C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds.
- Enzyme concentration
- MATLAB - Can easily be changed by inputting a value (in the range of 0-1 g/kg for each enzyme) into an interactive prompt. The flexibility is beneficial especially when investigating optimum operating conditions in the biorefinery.
- Kappa and Spatial Kappa - It is possible to change the number of enzyme agents by editing a separate file, which affects the relative concentration of enzymes (say, 3 times more of enzyme A than B). However, it would be non-trivial to translate that into an absolute value (e.g. 0.5 g of enzyme per 1kg of solution).
- C - Similarly to Kappa, this can easily be changed in relative terms.
- Strength of inhibition
- MATLAB - Incorporates inhibition of enzymes based on glucose and cellobiose concentrations; the strength can be changed. There is also scope for xylose inhibition, but it is set to zero in this model.
- Kappa and Spatial Kappa - The inhibition rates can be easily changed by editing a file with parameters.
- C - Incorporates inhibition of exoglucanase by individual cellobiose molecules based on spatial location. Could be extended to include inhibition by glucose; and also to have free glucose taken out of the system after it is made.
- Amount of raw material input
- MATLAB - An interactive prompt asks the user for an initial amount of cellulose.
- Kappa and Spatial Kappa - The initial amount of cellulose can be modified by editing a file. Also, in Spatial Kappa we ran experiments with adding more cellulose during the process.
- C - The amount can be passed as a command-line argument.
Computational cost
The MATLAB, C and Kappa models do their work in relatively short periods of time.
In contrast, the Spatial Kappa model takes a significant amount of time to run (about 30 minutes, depending on the settings of parameters). This is because when rules are translated from Spatial Kappa to the simulator, the complexity of the system increases. For a system with n compartments in d dimensions, one rule would need to be translated into n × d rules, to take into account possible spatial locations of agents. That increases the time taken to run a simulation by a factor of n × d. Fortunately, we had access to a computing cluster (ECDF, [http://www.ecdf.ed.ac.uk/ www.ecdf.ed.ac.uk]), where we could run 1,000 simulations in about 5 hours.
Representing reality
The MATLAB model is based on the empirical literature, and so should be the best representation of reality. Units of substrate is grams per kilogram (g/kg) and time is in hours. The kinetic rates are based on experimental data which gives the model some validity, however only within certain time limits.
However, since literature was not available for the synergistic system (with closely linked enzymes) we are considering, we had nothing to base a MATLAB model of synergy on. So, our only MATLAB model is the non-synergistic system.
The C and Spatial Kappa models were capable of comparing a synergistic and a non-synergistic system, but in both cases the model is highly abstract and based only on our understanding of the system due to unavailability of empirical data for dynamics of cellulose, cellobiose and glucose.
Conclusions
Although it is hard to compare the different approaches we took and even harder to choose and recommend the best one, our modelling gave us some important insights.
To begin with, we successfully modelled synergy in C and Spatial Kappa, so these models tell us that synergy is a viable option. In case of MATLAB, there is still potential to improve the model to show synergy (by adding more ODEs), whereas it would be at least very cumbersome to do the same in plain Kappa.
The MATLAB model should be the one most closely representing the real-world system. That is due to the fact that the model is built using experimentally adjusted values of constants and informed with known reaction equations. However, given sufficient data, it is also possible to adjust the Kappa / Spatial Kappa models to use different kinetic rates and concentrations of enzymes. It would require major modifications to achieve the same in the C model.
The stochastic route taken by the C and (Spatial) Kappa models means that multiple simulations need to be run and averaged in order to get a robust estimate of cellulose dynamics. Whereas this takes a relatively short time for the C and Kappa models, Spatial Kappa considerably increases the amount of time needed to do that.
We would say that, as a general conclusion, all of our approaches have their strong points and are suited to different tasks - the stochastic approaches show us how our system works, whereas the deterministic approach gives us some real numbers against which to test the system.
 "
"