Team:UT-Tokyo/Data/Modeling/Model01

From 2011.igem.org

(Difference between revisions)
 
(One intermediate revision not shown)
Line 1: Line 1:
-
{{:Team:UT-Tokyo/Templates/BeginContent|fullpagename=Team:UT-Tokyo/Data/Modeling/Model02|subpagename=Model02}}
+
{{:Team:UT-Tokyo/Templates/BeginContent|fullpagename=Team:UT-Tokyo/Data/Modeling/Model01|subpagename=Model1}}
-
=Model2: A simple model for E.coli chemotaxis=
+
=[[Team:UT-Tokyo/Data/Modeling|Modeling]]/Model1: L-Asp diffusion=
 +
 
 +
=[[Team:UT-Tokyo/Data/Modeling/Model01/applet|Interactive demo]]=
=Aim=
=Aim=
-
We tried to derive a simple relationship between Asp concentration and E.coli chemotaxis so that
+
It was required to know the behavior of L-Asp diffusion to perform our entire simulation (model3).
-
it become possible to simulate macroscopic (n~10<html><sup>8</sup></html>) E.coli-colony chemotactic behavior in the entire simulation.
+
We experimentally checked Asp diffusion using TLC method but the results were insufficient for the entire simulation.
-
 
+
So we decided to investigate the Asp diffusion by numerical simulation.
-
=Background=
+
-
SPECS <html><sup class="ref">[1]</sup></html> is one of the model simulating E.coli chemotactic behavior.
+
-
It considers internal condition of E.coli (receptor methylation etc) so it is a relatively strict taxis model.  It is suitable for semi-macroscopic simulation which has around ten thousand E.coli and the timescale is within a hour.
+
-
For our system, however, it takes too much time to replicate entire system, because the system includes much more E.coli(about one hundred of million) and the time scale is relatively long (a few days).
+
-
Therefore we devised a new model based on SPECS which requires less calculation amount.
+
=Method=
=Method=
-
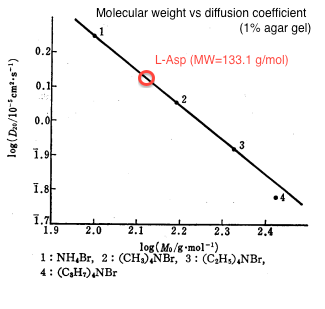
We approximated chemotactic motion of E.coli groups into two factors, that is, parallel translation and diffusion.
+
We estimated the value of diffusion coefficient by interpolating molecular mass of L-Asp (133) from the relationship between molecular weight and diffusion constant as shown in figure 1<html><sup class="ref">[1]</sup></html>.
-
Let 'V' represents a parallel translation velocity, 'D' represents a diffusion coefficient of E.coli groups and 'A' represents L-Asp concentration.
+
-
E.coli can detect A and its gradient ∇A.
+
-
They have an internal circuit to translate these signal into motions of their flagellum and try to run toward Asp-richer region.
+
-
So we thought V and D could be represented as a functions of A and ∇A.
+
-
And then we used SPECS model to derive these functions.
+
-
Here we introduce SPECS briefly.
+
{{:Team:UT-Tokyo/Templates/Image|file=utt_m1_fig1.png|caption=Figure 1. Molecular Weight v.s. Diffusion Constant (1% agar. gel)}}
-
An E.coli belongs to one of two mobile states: "Run" and "Tumble".
+
-
Run state indicates that E.coli goes straight until the state changes.
+
-
Tumble state indicates that E.coli is changing its direction and doesn't move around.
+
-
E.coli changes its state "Run" to "Tumble" with probability P<html><sub>rt</sub></html> [1/sec].
+
-
"Tumble" to "Run" with P<html><sub>tr</sub></html> [1/sec].
+
-
These probability depend on the E.coli internal state.
+
-
The internal state is represented as two variables: "a" and "m".
+
-
"a" indicates its kinase activity and "m" represents its receptor's methylation level.
+
-
They vary depending on L-Asp concentration.
+
-
In addition, SPECS concern the Brownian fluctuation.
+
-
From these modeling, SPECS can replicate the internal circuit of E.coli which translates Asp concentration distribution into its mobile state.
+
-
We processed Monte Carlo simulation for 20000 E.coli which behavior was based on SPECS in some different Asp concentration and its gradient strength.  The shape of the Asp gradient we used were exponential.
+
The estimated value was D = 0.001 [<html>mm<sup>2</sup>/sec</html>].
 +
We used 0.25% agar gel in our experiment and according to the previous study<html><sup class="ref">[2]</sup></html>, there is no practical difference of diffusion coefficient between 1% and 0.25% agar gel.
-
[[File:utt_m2_eqn1.png]]
+
We simulated the time development of the L-Asp concentration distribution.
 +
We simulated the diffusion equation using 1st order finite difference method.
-
We approximated E.coli movement as the combination of parallel translation and diffusion.
+
[[File:utt_m1_eqn1.png]]
-
We recorded the time course of average position <x> and root-mean-square \<x^2> and then
+
-
calculated average velocity
+
-
[[File:utt_m2_eqn2.png]]
+
A indicates the L-Asp concentration and D means the diffusion coefficient.
-
 
+
The shape of system was a circle with radius 5cm.
-
and the diffusion constant.
+
We dropped 2&times;10<html><sup>-7</sup></html> mol Asp at the center of the circle as the initial state.
-
 
+
-
[[File:utt_m2_eqn3.png]]
+
-
 
+
-
We derived the relationship between
+
-
* Asp concentration and average velocity of E.coli
+
-
* Asp concentration and diffusion constant of E.coli
+
-
* gradient of Asp concentration and average velocity of E.coli
+
-
* gradient of Asp concentration and diffusion constant of E.coli
+
-
Finally we fitted approximated curve (represented as functions of A and ∇A) to these data so that we could use these functions in the entire simulation.
+
=Result=
=Result=
-
 
+
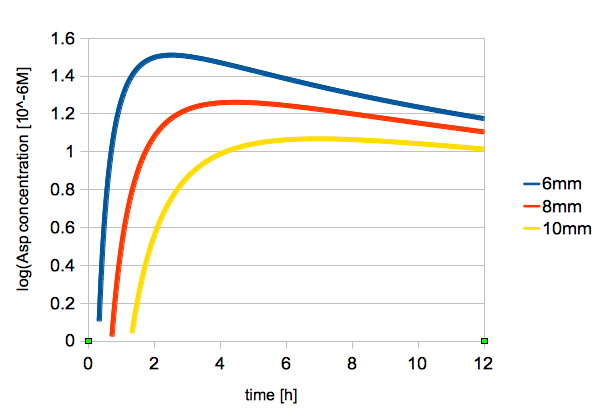
The time change of logarithmic values of L-Asp concentration at 2, 6, 8 mm from the center is shown in figure 3.
-
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig1.png|caption=Figure 1. relationship between Asp conc. and avg. velocity}}
+
{{:Team:UT-Tokyo/Templates/Image|file=utt_m1_fig2.png|caption=Figure 3. Change in L-Asp Concentration Over Time (2, 6, 8 mm from the center)}}
-
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig2.png|caption=Figure 2. relationship between gradient of Asp conc. and avg. velocity}}
+
-
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig3.png|caption=Figure 3. relationship between Asp conc. and diffusion coef}}
+
-
{{:Team:UT-Tokyo/Templates/Image|file=utt_m2_fig4.png|caption=Figure 4. relationship between gradient of Asp conc. and diffusion coef}}
+
-
 
+
-
The fitted curves are represented by following equation.
+
-
 
+
-
[[File:utt_m2_eqn4.png]]
+
-
 
+
-
[[File:utt_m2_eqn5.png]]
+
<html>
<html>
Line 71: Line 34:
<div id="references">
<div id="references">
<ul>
<ul>
-
   <li id="ref_1">[1] Jiang L, Ouyang Q, Tu Y (2010) Quantitative Modeling of Escherichia coli Chemotactic Motion in Environments Varying in Space and Time. PLoS Comput Biol 6(4): e1000735. doi:10.1371/journal.pcbi.1000735</li>
+
   <li id="ref_1">[1] Toshiko M, Masayuki N "measurement of diffusion coefficient using agar. gel" Chemical Society of Japan, 1978, 26, 5, 377</li>
 +
  <li id="ref_2">[2] W. Derbyshire, I. D. Duff "N.m.r of Agarose Gels" Chem. Soc., 1974, 57, 243-254</li>
</ul>
</ul>
</div>
</div>
</html>
</html>
{{:Team:UT-Tokyo/Templates/EndContent}}
{{:Team:UT-Tokyo/Templates/EndContent}}

Latest revision as of 20:51, 5 October 2011

Modeling/Model1: L-Asp diffusion

Interactive demo

Aim

It was required to know the behavior of L-Asp diffusion to perform our entire simulation (model3). We experimentally checked Asp diffusion using TLC method but the results were insufficient for the entire simulation. So we decided to investigate the Asp diffusion by numerical simulation.

Method

We estimated the value of diffusion coefficient by interpolating molecular mass of L-Asp (133) from the relationship between molecular weight and diffusion constant as shown in figure 1[1].

Figure 1. Molecular Weight v.s. Diffusion Constant (1% agar. gel)
Figure 1. Molecular Weight v.s. Diffusion Constant (1% agar. gel)

The estimated value was D = 0.001 [mm2/sec]. We used 0.25% agar gel in our experiment and according to the previous study[2], there is no practical difference of diffusion coefficient between 1% and 0.25% agar gel.

We simulated the time development of the L-Asp concentration distribution. We simulated the diffusion equation using 1st order finite difference method.

Utt m1 eqn1.png

A indicates the L-Asp concentration and D means the diffusion coefficient. The shape of system was a circle with radius 5cm. We dropped 2×10-7 mol Asp at the center of the circle as the initial state.

Result

The time change of logarithmic values of L-Asp concentration at 2, 6, 8 mm from the center is shown in figure 3.

Figure 3. Change in L-Asp Concentration Over Time (2, 6, 8 mm from the center)
Figure 3. Change in L-Asp Concentration Over Time (2, 6, 8 mm from the center)

References

  • [1] Toshiko M, Masayuki N "measurement of diffusion coefficient using agar. gel" Chemical Society of Japan, 1978, 26, 5, 377
  • [2] W. Derbyshire, I. D. Duff "N.m.r of Agarose Gels" Chem. Soc., 1974, 57, 243-254

Retrieved from "http://2011.igem.org/Team:UT-Tokyo/Data/Modeling/Model01"