Team:Edinburgh/Phage Replication
From 2011.igem.org
(Difference between revisions)
| Line 18: | Line 18: | ||
| - | + | '''Phage dynamic model''' | |
*'''dx/dt=ax-bvx ''' | *'''dx/dt=ax-bvx ''' | ||
| Line 41: | Line 41: | ||
| - | + | '''Simulations''' | |
The [[:File:Matlab_code_phagerep.txt | MATLAB code]] uses a <span class="hardword" id="rk">Runge-Kutta method</span> of order four to solve the system. | The [[:File:Matlab_code_phagerep.txt | MATLAB code]] uses a <span class="hardword" id="rk">Runge-Kutta method</span> of order four to solve the system. | ||
| Line 57: | Line 57: | ||
:3. Production, which refers to glucose here, inhibits the action of the above enzymes. | :3. Production, which refers to glucose here, inhibits the action of the above enzymes. | ||
| - | + | '''Cellulase model''' | |
| - | + | ||
| + | '''Simulation''' | ||
[[File:Cellulase.jpg|center|thumb|700px|caption|]] | [[File:Cellulase.jpg|center|thumb|700px|caption|]] | ||
Revision as of 11:13, 7 September 2011
Phage Replication
A basic activity in biorefinery consists of the degradation of cellulose, due to the presence of enzymes. We are not only concerned with the activities and the amount of enzymes, but also with metabolism and activities of bacteriophage.
M13 Replication
- The M13 phage attacks E. coli (host), multiplies in the host cell cytoplasm, and is released without causing the bacteria’s death (non-lytic).
Phage dynamic model
- dx/dt=ax-bvx
- (Rate of change of quantity of uninfected E. coli equals to the uninfected E. coli replicate itself minus the E. coli infected by M13 phage.)
- dy/dt=ay+bvx
- (Rate of change of quantity of infected E. coli equals to the quantity of infected E. coli replicate itself plus the E. coli infected by M13 phage.)
- dv/dt=cy-bvx-mv
- (Rate of change of quantity of free phage equals to the phage released by infected E. coli minus the phage which is to infect an E. coli and the decayed phage.)
- X(t) — uninfected E. coli
- Y(t) — infected E. coli
- V(t) — free phage
- a — replication coefficient of E. coli
- b — transmission coefficient of phage
- c — replication coefficient of phage
- m — decay rate of phage
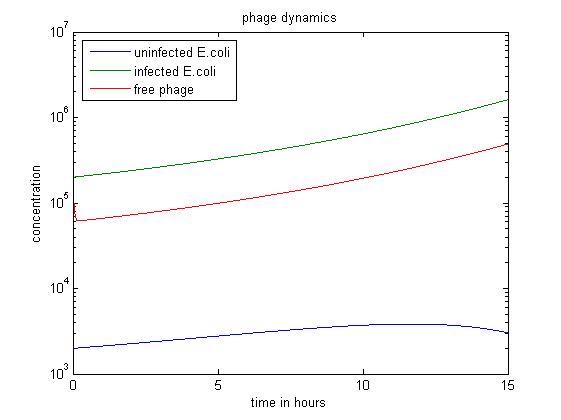
Simulations
The MATLAB code uses a Runge-Kutta method of order four to solve the system.
- The above figure shows a simulation going over 15 hours.
- The simulation shows the infected E. coli population dominates. And the phage population decreases at first then increases.
Synergy on each phage
The synergy function, which means having enzymes closer together, is supposed to increase the efficiency of cellulose degradation. We attempted to construct a model of cellulase with regard of synergy.
For the model we construct, we assume that
- 1. Endoglucanase cuts cellulose chains in the middle,exoglucanase chews away at the end of a cellulase chain, they work together to produce cellobiose.
- 2. Because of the proximity of the β-glucosidase and the other two enzymes, as well as the sufficient amount of β-glucosidase on each phage, we assume the mdiate production, cellobiose, is all converted to glucose.
- 3. Production, which refers to glucose here, inhibits the action of the above enzymes.
Cellulase model
Simulation
References
- Slonczewski JL, Foster JW (2010) [http://www.wwnorton.com/college/biology/microbiology2/ch/11/etopics.aspx Microbiology: An Evolving Science], 2nd edition. W. W. Norton & Company
- Robert J.H Payne, Vincent A. A. Jansen(2011)[ http://personal.rhul.ac.uk/ujba/115/jtb01.pdf: Understanding Bacteriaphage therapy as a density-dependent kinetic process]
- Cattoen C (2003) [http://msor.victoria.ac.nz/twiki/pub/Groups/GravityGroup/PreviousProjectsInAppliedMathematics/bacteria-phage_REPORT.pdf: Bacteriaphage mathematical model applied to the cheese industry]
 "
"