Team:Imperial College London/Project/Chemotaxis/Results
From 2011.igem.org
| Line 26: | Line 26: | ||
<p>The model based on Spiro et al. (1997) [1] was used to identify candidates of the chemotaxis receptor pathway. The methylation level of receptors, phosphorylation level of CheY and CheB were studied from Spiro’s model(Figure 2-Figue3). With receptor concentration per cell equals to 8x10<sup>-6</sup>mole/L, the lower threshold concentration of chemoattractant that the bacterium start to detect is 10<sup>-8</sup>mole/L. The saturation level is 10<sup>-6</sup>mole/L in which concentration or higher the bacteria’s movements to chemoattractant are less efficient. In addition, the relation between chemoreceptor concentration and the lower threshold and staturation level were also studied (Figure 5). </p> | <p>The model based on Spiro et al. (1997) [1] was used to identify candidates of the chemotaxis receptor pathway. The methylation level of receptors, phosphorylation level of CheY and CheB were studied from Spiro’s model(Figure 2-Figue3). With receptor concentration per cell equals to 8x10<sup>-6</sup>mole/L, the lower threshold concentration of chemoattractant that the bacterium start to detect is 10<sup>-8</sup>mole/L. The saturation level is 10<sup>-6</sup>mole/L in which concentration or higher the bacteria’s movements to chemoattractant are less efficient. In addition, the relation between chemoreceptor concentration and the lower threshold and staturation level were also studied (Figure 5). </p> | ||
<p>The quantity that links the CheY-p concentration with the type of motion (run vs. tumble) is called bias. It is defined as the fraction of time spent on the directed movement with respect to the total movement time. The relative concentration of CheYp is converted into motor bias using a Hill function (Euqation 1)[5]. A graph describes bias against CheY-p concentration was shown in Figure 5.</p> | <p>The quantity that links the CheY-p concentration with the type of motion (run vs. tumble) is called bias. It is defined as the fraction of time spent on the directed movement with respect to the total movement time. The relative concentration of CheYp is converted into motor bias using a Hill function (Euqation 1)[5]. A graph describes bias against CheY-p concentration was shown in Figure 5.</p> | ||
| - | <p> | + | <p> <img src="https://static.igem.org/mediawiki/2011/thumb/4/4a/1.png/800px-1.png" width="500" height="200" /> |
<br> | <br> | ||
<p> <img src="https://static.igem.org/mediawiki/2011/thumb/f/fb/2.png/800px-2.png" /> | <p> <img src="https://static.igem.org/mediawiki/2011/thumb/f/fb/2.png/800px-2.png" /> | ||
| Line 41: | Line 41: | ||
<br> | <br> | ||
</p> | </p> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Revision as of 16:20, 6 September 2011
Chemotaxis Results
Modelling
Introduction
E.coli is a motile strain of bacteria, which is to say it can swim. It is able to do so by rotating its flagellum, which is a rotating tentacle like structure on the outside of cell. Chemotaxis is the movement up concentration gradient of chemoattractants (i.e. malate in our project) and away from poisons. E.coli is too small to detect any concentration gradient between the two ends of itself, and so they must randomly head in any direction and then compare the new chemoattractant concentration at new point to the previous 3-4s point. Its motion is described by ‘runs’ and ‘tumbles’, runs refer to a smooth, straight line movement for a number of seconds, while tumble referring to reorientation of bacteria [1]. Chemoattractant increases transiently raise the probability of ‘tumble’ (or bias), and then a sensory adaptation process returns the bias to baseline, enabling the cell to detect and respond to further concentration changes. The response to a small step change in chemoattractant concentration in a spatially uniform environment increase the response time occurs over a 2- to 4- s time span [2]. Saturating changes in chemoattractant can increase the response time to several minutes.
Many bacterial chemoreceptors belong to a family of transmemberane methyl-accepting chemotaxis proteins (MCPs) [3]. Each chemoreceptors on the bacterium has a periplasmic binding domain and a cytoplasmic signaling domain that communicates with the flagellar motors via a phosphorelay sequence involving the CheA, CheY, and CheZ proteins. Modeling of this chemotaxis pathway in single cell is very important, as it will help us to determine, with certain numbers of chemoreceptors, the threshold of chemoattractant concentration where the bacterium is able to detect and the saturation level of chemoattractant where the all the receptors on the bacterium are occupies. A it is believed that the auxin should be kept at a very close region around the root (0.25 cm [4]), therefore it is very important to obtain the number of chemoreceptors needed on individual bacterium that enables the it to stay close to the plant root/seed from modeling.
In addition, modeling of chemotaxis of bacteria population is also valuable for us to capture the overview of movement of bacteria around the plant root; therefore it can potentially inform our project about how and where we can place our bacteria. Under experiment condition, the chemoattractant diffuses all the time from the source. However, in real soil, the root produces malate all the time, therefore we assume that the distribution of chemoattractant outside the root is steady and time-independent. Hence, the modeling of bacteria population chemotaxis will be built with different patterns of chemoattractant distributions.
Chemotaxis Pathway
The chemotaxis pathway in E.Coli is demonstrated in Figure 1. MCPs form stable ternary complexes with the CheA and CheW proteins to generate signals that control the direction of rotation of the flagellar motors [5]. The signaling currency is in the form of phosphoryl groups (p), made available to the CheY and CheB effector proteins through autophosphorylation of CheA[1].CheY-p initiates flagellar responses by interacting with the motor to enance the probability of ‘run’ [1]. CheB-p is part of a sensory adaptation circuit that terminates motor responses [1]. MCP complexes have two alternative CheA autokinase activity; When the receptor is not occupied by chemoattractant, the receptor stimulates CheA activity [1]. The overall flux of phosphoryl groups to inhibited and stimulated states. Changes in attractant concentration shift this distribution, triggering a flagellar response [1]. The ensuing changes in CheB phosphorylation state alter its methylesterase activity, producing a net change in MCP methylation state that cancels the stimulus signal [1]. Therefore, studying of methylation level, phosphorylation level of CheB and CheY are important to understand chemotaxis of single cell.

Figure 1[1]: Chemotaxis signaling conponents and oathways for E.Coli.
The model based on Spiro et al. (1997) [1] was used to identify candidates of the chemotaxis receptor pathway. The methylation level of receptors, phosphorylation level of CheY and CheB were studied from Spiro’s model(Figure 2-Figue3). With receptor concentration per cell equals to 8x10-6mole/L, the lower threshold concentration of chemoattractant that the bacterium start to detect is 10-8mole/L. The saturation level is 10-6mole/L in which concentration or higher the bacteria’s movements to chemoattractant are less efficient. In addition, the relation between chemoreceptor concentration and the lower threshold and staturation level were also studied (Figure 5).
The quantity that links the CheY-p concentration with the type of motion (run vs. tumble) is called bias. It is defined as the fraction of time spent on the directed movement with respect to the total movement time. The relative concentration of CheYp is converted into motor bias using a Hill function (Euqation 1)[5]. A graph describes bias against CheY-p concentration was shown in Figure 5.


Figure 2: [Phosphorylated CheY]/ [CheY]

Figure 3: [Phosphorylated CheY]/ [CheY]

Figure 4: [Phosphorylated CheB]/ [CheB]

Figure 6: The dependency of Bias on the concentration of CheY-p
Simulation of chemotaxis of bacteria population
The part of modeling focused on creating the movement model of bacteria population for chemotaxis. In order to accurately built this model, the following assumptions are made based on literature:
1) During the directed movement phase, the mean speed of an E. coli equals 24.1 μm/s, varying speed between 17.3 μm/s and 30.9 μm/s [7]. Whereas during the tumbling phase, the speed is significantly smaller and can be neglected.
2) E.Coli usually take previous second as their basis on deciding whether the concentration has increased or not. Therefore, in our model the bacteria will be able to compare the concentration of chemattractant at t second and t-1 second.
3) In our model, we ignored that E.Coli do not travel in straight line during run, but take curved paths due to unequal firing of flagella.
4) Our model did not consider the size changing and dividing of bacteria. And the tendency of bacteria congregate into small area due to qurum sensing is also ignored.
Model Designing
In chemotaxis, receptors sensing an increase in the concentration of chemoattractant send a signal that suppresses tumbling, and, simultaneously, the receptor becomes more highly methylated. Conversely, a decrease in the chemoattractant concentration increases the tumble frequency and causes receptor demethylation. The tumbling frequency is approximately 1 Hertz, and decreased to almost zero as he bacteria move up a chemtoatic gradient [5].
In the model, the bacteria should be able compare the chemoattractant concentration at current point to the concentration at previous second. If the concentration decreases (i.e. C_t1-C_t2 ≤0), the bacteria will tumble with frequency 1 Hertz. If the concentration increases (C_t1-C_t2 >0), the tumble frequency decreases, and hence the probability of tumbling decreases. From equation 10 in ref [6], we known that even if C_t1-C_t2 >0, the probability of tumbling could decreases to 39%. Therefore, we can conclude the above description into the following statement [8]:

Chemotaxis of bacteria population under laboratory conditions
Under laboratory condition, the chemoattractant diffuses from the source, hence the distribution pattern of chemoattratctant changes with time. In this case, error function (Equation 2) was used to describe the non-steady chemoattractant distribution. The simulation of chemotaxis of 100 bacteria placed 6cm away from the 5mM malate is shown in the movie below.

Chemotaxis of bacteria population in Soil
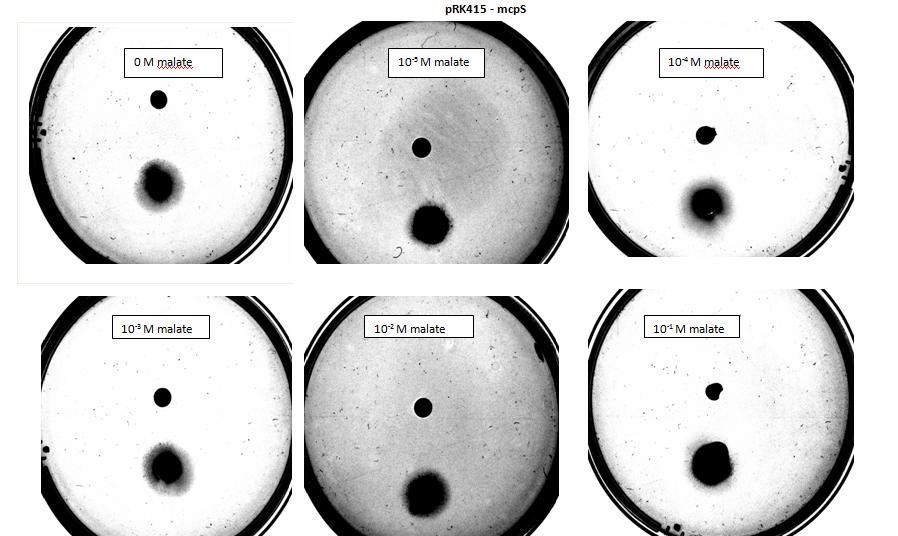
Malate is used as the chemoattractant in our project, the malate is constantly secreted in the root tip, and the concentration is 0.3mM[9]. In this case, the malate source is always replenished due to continuous secretion from the root tip, the distribution pattern can be considered as steady (i.e. independent of time), and steady state Keler-Segel model was used to demonstrate this distribution (Equation 3 and Equation 5). The distribution was displayed in Figure 7. And Figure 8 shows the position of lower threshold where the bacteria start to response to malate and the saturation level where the chemoreceptors start to loss efficiency. Finally, the animation of bacterial chemotaxis in steady chemoattractant distribution is demonstrated in video below.



Reference
[1] Peter A. Spiro, John S. Parkinson, Hands G. Othmer. ‘A model of exciatation and adaptation in bacterial chemotaxis’. Proc. Natl. Acd. Sci. USA, Vol. 94, pp. 7263-7268, July 1997. Biochemistry
[2] Blocks S. M., Segall J. E. and Berg H.C. (1982) Cell 31, 215-226.
[3] Stock J. B. and Surette M. G. (1996) ‘Escherichia coli and salmonella: Cellular and molecular biology’. Am. Soc. Microbiol., Washington, DC).
[4] Andrea Schnepf. ‘3D simulation of nutrient uptake’
[5] M D Levin, C J Morton-Firth, W N Abouhamad, R B Bourret, and D Bray, ‘Origins of individual swimming behavior in bacteria.’
[6] Vladimirov N, Lovdok L, Lebiedz D, Sourjik V (2008) ‘Dependence of Bacterial Chemotaxis on Gradient Shape and Adaptation Rate’ PloS Comput Biol 4(12): e1000242. Doi:10.1371/journal.pcb1.1000242.
[7] Zenwen Liu and K. Papadopoulos. ‘Unidirectional Motility of Escherichia coli’. APPLIED AND ENVIRONMENTAL MICROBIOLOGY, Oct. 1995, p. 3567–3572 Vol. 61, No. 100099-2240/95/$04.0010 Copyright q 1995, American Society for Microbiology
[8] https://2009.igem.org/Team:Aberdeen_Scotland/chemotaxis
[9] Enrico Martinoia and Doris Rentsch. ‘Malate Compartmentation-Responses to a Complex Metabolism’ Annual Review of Plant Physiology and Plant Molecular Biology Vol. 45: 447-467 (Volume publication date June 1994) DOI: 10.1146/annurev.pp.45.060194.002311
[10] C.J. Brokaw. ‘Chemotaxis of bracken spermatozoids: Implications of electrochemical orientation’.
[11] D.L.Jones, A.M. Prabowo, L.V.Kochian, ‘Kinetics of malate transport and decomposition in acid soils and isolated bacterial populations the effect of microorganisms on root exudation of malate under Al stress.’ Plant and Soil 182:239-247, 1996.
Malate concentration distribution
For our project, malate is the chemoattractant that results in the movement of E.coli. In this section, we will first model the concentration distribution of the chemoattractant, malate in the soil. Then, we will model the bacteria concentration pattern as a result of this distribution of malate. Finally, we will infer some useful information by analysing the results of the modelling.
We will model the concentration distributions of malate and bacteria using the Keller-Segel model which is governed by the two equations shown below. Solving the equations will give the concentration distributions of the malate and the bacteria respectively
 ---------------------------------------------------------------------------------------------(1)
---------------------------------------------------------------------------------------------(1)
 -------------------------------------------------------(2)
-------------------------------------------------------(2)
s = concentration of chemoattractant
D = diffusion coefficient of chemoattractant
f = degradation of chemoattractant
b = number concentration of bacteria
µ = bacterial diffusion coefficient (how fast bacteria spread)
χ = chemotactic coefficient (how sensitive bacteria are)
g = bacterial cell growth
h = bacterial cell death
The values of the above parameters for E. coli are shown in the following table. These values will be used for the modelling.
Parameter description |
Notation |
Value |
Initial bacterial concentration |
b0 |
108 cells/ml |
Initial attractant concentration |
s0 |
0.1 mM or 0.1 mol/m3 |
Bacterial diffusion coefficient |
µ |
1.5*10-5 cm2/s |
Bacterial chemotactic coefficient |
χ |
1.5-75*10-5 cm2/s |
Attractant diffusion coefficient |
D |
10-5 cm2/s |
Reference: Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis II: Bacterial Populations
The assumptions that we have made are as follow:
- The entire root system is assumed to take the shape of a long cylinder. Hence, a cylindrical coordinate system will be used.
- The system is axisymmetric and there is no variation along the vertical length of the root. Hence,

- The system has reached steady state and is time-independent. Hence,

- Degradation of chemoattractant is first order and is described by f = ks where k is the degradation rate of the chemoattractant.
- Bacterial cell growth and death are neglected. Hence, g(b,s) = h(b,s) = 0
Applying the assumptions above, equation (1) becomes
![]()
Rearranging,
![]() -------------------------------------------------(3)
-------------------------------------------------(3)
Equation (3) is in the form of the modified Bessel equation. Hence, the solution of equation (3) is given by,
![]()
Where K0 is the modified Bessel function.
Since it is unrealistic for the concentration to increase to infinity, A=0. And applying the boundary condition, the solution becomes,
![]() -----------------------------------------------------(4)
-----------------------------------------------------(4)
The modeling result show that the steady-state pattern of malate distribution. The concentration of malate is a variable against the distance


 "
"