Team:Imperial College London/Project/Chemotaxis/Results
From 2011.igem.org
| Line 115: | Line 115: | ||
-gibson assembly of 22&23 fragments. | -gibson assembly of 22&23 fragments. | ||
-Due to this we have transformed 5a strain with a high copy plasmid containing ampicillin and kanamycin resistance (AK3 backbone)and sfGFP. These cells have been numbered 17.</p> | -Due to this we have transformed 5a strain with a high copy plasmid containing ampicillin and kanamycin resistance (AK3 backbone)and sfGFP. These cells have been numbered 17.</p> | ||
| + | <h>Testing</h1> | ||
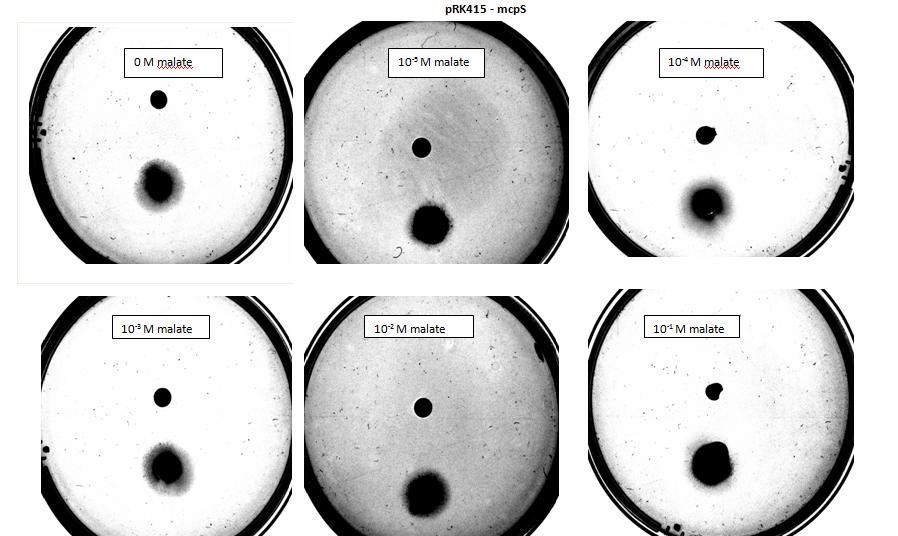
| + | <p>Testing for chemotaxis can be split into qualitative and quantitative assays. Qualitative assays involve putting engineered <i>E. coli</i> and an attractant onto semi-solid agar plates and observe the movement of the microbes. If they can be observed to move towards the attractant source, they are likely to be attracted to the ligand. In quantitative assays, capillaries are filled with different concentrations of the attractant malate. Positive controls are provided by filling identical capillaries with different concentrations of serine, which <i>E. coli</i> naturally move towards. Negative controls are provided by filling capillaries with media that does not contain a source of attractant. The amount of bacteria that swim into each capillary is evaluated by FACS.</p> | ||
| + | |||
| + | <p> For simplicity, we will be working with Arabidopsis to observe the uptake of bacteria into plant roots. | ||
| + | Arabidopsis thaliana is a common plant model organism. It belongs to the mustard family and fulfils many important requirements for model organisms. As such, its genome has been almost completely sequenced and replicates quickly, producing a large number of seeds. It is easily transformed and many different mutant strains have been constructed to study different aspects (National Institute of Health, no date). While Arabidopsis may not represent plant populations naturally occurring in arid areas threatened by desertification, it is a handy model organism we will be using to study the effect of auxin on roots, observe chemotaxis towards them and look at uptake of bacteria into the roots. | ||
| + | We will be using Arabidopsis to look at the uptake of our engineered bacteria into the plants. For this, we will be using wild type Arabidopsis and E. coli that constitutively express green fluorescent protein. The natural fluorescence produced by plant roots and green fluorescence produced by the bacteria can be used to image the uptake of bacteria using confocal microscopy. | ||
| + | |||
| + | |||
<h2>Chapter 2 bacteria uptake into roots</h2> | <h2>Chapter 2 bacteria uptake into roots</h2> | ||
| Line 355: | Line 363: | ||
<b>Capillary assay</b> | <b>Capillary assay</b> | ||
<p> quantitative, bacterial movement into a syringe/capillary based on attraction, number of bacteria measured in a capillary after 30min using FACS machine. motility medium & high bacterial OD used..</p> | <p> quantitative, bacterial movement into a syringe/capillary based on attraction, number of bacteria measured in a capillary after 30min using FACS machine. motility medium & high bacterial OD used..</p> | ||
| - | </html> | + | <h2>2. Tests for uptake of bacteria into roots</h2> |
| + | <h2>Wednesday, 3 August 2011</h2> | ||
| + | <p>One important part of our project is uptake of our bacteria into plant roots. The observation that this occurs (albeit under controlled lab settings) is new and was only published last year. We attempted to replicate these findings.</p> | ||
| + | |||
| + | <p>In preparation, we met with Dr Martin Spitaler who advised us on how to prepare samples for the confocal microscopy. Confocal microscopy is much more precise than conventional light field microscopy as it eliminates background light by focusing the laser through a pinhole (Mark Scott, oral communication). The confocal microscopy will focus on imaging GFP expressing bacteria inside Arabidopsis roots to show that uptake of the bacteria takes place. </p> | ||
| + | |||
| + | <p>Staining of wt roots with DiD, a lipophilic dye that stains the plant membranes and does not interfere with the absorption or emission spectra of GFP and Dendra, was unsuccessful. However, natural fluorescence was measured in a root in a spectrum that does not interfere with measuring GFP. We should therefore not need to dye the roots before imaging.</p> | ||
| + | |||
| + | <iframe width="420" height="345" src="http://www.youtube.com/embed/EqLCzVaBGI0?rel=0" frameborder="0" allowfullscreen></iframe><iframe width="420" height="345" src="http://www.youtube.com/embed/Q60tsCjfH4c?rel=0" frameborder="0" allowfullscreen></iframe> | ||
| + | |||
| + | <p><i>Stack of wt Arabidopsis root. The root can be imaged at around 488nm. Imaging carried out by Dr Martin Spitaler.</i></p> | ||
| + | |||
| + | <p>We may also try to stain the roots with propidium iodide, which is also a strong indicator of cell wall break down. </p> | ||
| + | |||
| + | <h2>Thursday, 4 August 2011</h2> | ||
| + | <p>We prepared the GFP-expressing bacteria for plant infection. They were spun down and media was exchanged prior to incubation at 37°C to reach exponential phase. Bacteria were then spun down and resuspended in wash buffer (5mM MES) to reach OD 30. 8ml, 4ml and 2ml were added to separate flasks, containing 100ml of half-MS media each. 4ml and 6ml of wash buffer were added to the flasks containing 4ml and 2ml bacteria, respectively. 8ml of wash buffer was added to the negative control. Ten Arabidopsis seedlings were distributed into each of the flasks. Incubation was carried out for 15 hours prior to imaging.</p> | ||
| + | |||
| + | <h2>Friday, 5 August 2011</h2> | ||
| + | <p>Prior to imaging, roots were washed in PBS to wash off bacteria and facilitate imaging. We imaged the plants incubated with 8ml of bacteria and were able to find bacteria inside one of the roots. A 3D picture was taken of uninfected roots and roots containing bacteria by taking a Z stackk image using confocal microscopy. </p> | ||
| + | |||
| + | <iframe width="425" height="349" src="http://www.youtube.com/embed/BBqXWjh8D54?rel=0" frameborder="0" allowfullscreen></iframe> | ||
| + | |||
| + | <p><i>This video shows a zoom from the top to the bottom of the root. It was put together from successive images taken at different depth levels. The GFP-expressing bacteria are clearly visible within the root.</i></p> | ||
| + | <p>We also imaged roots that did not contain bacteria via a similar Z-stack scan. This image is shown below.</p> | ||
| + | <iframe width="420" height="345" src="http://www.youtube.com/embed/SEqt6y749ZQ?rel=0" frameborder="0" allowfullscreen></iframe> | ||
| + | |||
| + | </html> | ||
Revision as of 13:02, 4 September 2011
Chemotaxis Results
Modelling
Two main aspects were modelled for our chemotaxis module: malate distribution in soil and the threshold concentration of malate needed to trigger chemotaxis.
The malate concentration distribution was modelled using the Keller-Segel model.
E.coli is a motile strain of bacteria, which is to say it can swim. It is able to do so by rotating its flagellum, which is a rotating tentacle like structure on the outside of cell. Chemotaxis is the movement up concentration gradient of chemoattractants (i.e. malate in our project) and away from poisons. E.coli is too small to detect any concentration gradient between the two ends of itself, and so they must randomly head in any direction and then compare the new chemoattractant concentration at new point to the previous 3-4s point. Its motion is described by ‘runs’ and ‘tumbles’, runs refer to a smooth, straight line movement for a number of seconds, while tumble referring to reorientation of bacteria [1]. Chemoattractant increases transiently raise the probability of ‘tumble’ (or bias), and then a sensory adaptation process returns the bias to baseline, enabling the cell to detect and respond to further concentration changes. The response to a small step change in chemoattractant concentration in a spatially uniform environment increase the response time occurs over a 2- to 4- s time span [2]. Saturating changes in chemoattractant can increase the response time to several minutes.
Malate concentration distribution
For our project, malate is the chemoattractant that results in the movement of E.coli. In this section, we will first model the concentration distribution of the chemoattractant, malate in the soil. Then, we will model the bacteria concentration pattern as a result of this distribution of malate. Finally, we will infer some useful information by analysing the results of the modelling.
We will model the concentration distributions of malate and bacteria using the Keller-Segel model which is governed by the two equations shown below. Solving the equations will give the concentration distributions of the malate and the bacteria respectively
 ---------------------------------------------------------------------------------------------(1)
---------------------------------------------------------------------------------------------(1)
 -------------------------------------------------------(2)
-------------------------------------------------------(2)
s = concentration of chemoattractant
D = diffusion coefficient of chemoattractant
f = degradation of chemoattractant
b = number concentration of bacteria
µ = bacterial diffusion coefficient (how fast bacteria spread)
χ = chemotactic coefficient (how sensitive bacteria are)
g = bacterial cell growth
h = bacterial cell death
The values of the above parameters for E. coli are shown in the following table. These values will be used for the modelling.
Parameter description |
Notation |
Value |
Initial bacterial concentration |
b0 |
108 cells/ml |
Initial attractant concentration |
s0 |
0.1 mM or 0.1 mol/m3 |
Bacterial diffusion coefficient |
µ |
1.5*10-5 cm2/s |
Bacterial chemotactic coefficient |
χ |
1.5-75*10-5 cm2/s |
Attractant diffusion coefficient |
D |
10-5 cm2/s |
Reference: Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis II: Bacterial Populations
The assumptions that we have made are as follow:
- The entire root system is assumed to take the shape of a long cylinder. Hence, a cylindrical coordinate system will be used.
- The system is axisymmetric and there is no variation along the vertical length of the root. Hence,

- The system has reached steady state and is time-independent. Hence,

- Degradation of chemoattractant is first order and is described by f = ks where k is the degradation rate of the chemoattractant.
- Bacterial cell growth and death are neglected. Hence, g(b,s) = h(b,s) = 0
Applying the assumptions above, equation (1) becomes
![]()
Rearranging,
![]() -------------------------------------------------(3)
-------------------------------------------------(3)
Equation (3) is in the form of the modified Bessel equation. Hence, the solution of equation (3) is given by,
![]()
Where K0 is the modified Bessel function.
Since it is unrealistic for the concentration to increase to infinity, A=0. And applying the boundary condition, the solution becomes,
![]() -----------------------------------------------------(4)
-----------------------------------------------------(4)
The modeling result show that the steady-state pattern of malate distribution. The concentration of malate is a variable against the distance


Chemotaxis
1. Signal pathway of a single bacterium
- the signal transfer inside the bacterium
chemoattractant stimulation -> chemoreceptor -> CheA -> CheY-P -> flagellar motor -> changed switching frequency between swimming and tumbling (biasing fraction) - the phosphrylation level of CheY can indicate the signal transferring pathway, the CheY-P concentration increases when the chemoreceptor is triggered
- the modeling result will show the optimal concentration to trigger the chemoreceptors (10-6 mol/L)
high = saturated chemoreceptors
low = cannot be detected



2. Bacterial population dynamics
An animation is made to show the movement of the population:
mainly by diffusion, biased motion with the presence of chemoattractant
based on the malate distribution in steady-state and the Spiro model
 "
"