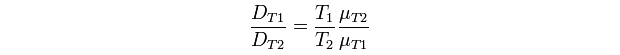Team:Edinburgh/Model Comparison

Model Comparison

The approaches

• MATLAB - Within the reactor tasked with degrading cellulose into glucose in the biorefinery, temperature, enzyme concentration, substrate reactivity as well as xylose, cellobiose and glucose inhibition all govern the amount of glucose product. Deterministic modelling using a set of ordinary differential equations highlights the essential kinetic relationship among the enzymes, exo/endo-glucanase and β-glucosidase. By solving these governing equations using the numerical tool MATLAB the level of degradation of cellulose is qualitatively predicted.

• Kappa - As an alternative, stochastic models were created using the Kappa language. The system is defined in terms of many discrete agents and rules of their interaction. The Kappa simulator then uses probabilistic equations to simulate the evolution of the system, incorporating an indeterministic element into the system.

• Spatial Kappa - Because of problems with the Kappa language, we decided to use a spatial extension developed by the Edinburgh 2010 iGEM team. This adds extra functionality to the language by introducing the concept of space.

• C model - Intended more as a demonstration of synergy than an accurate model of the world, the cellulose is represented using a simple two-dimensional grid, on which enzymes move using Brownian motion. This is an ad hoc model made in a general programming language. It was inspired by cellular-automata systems, though cannot really be considered one.

Comparison criteria

We chose the following criteria which are desirable in a model. They also show the main differences and similarities among our models, however the list is non-exhaustive.

Flexibility

We define flexibility as the capacity of a model to adopt different initial conditions. For example temperature, mass of substrate, strength of inhibition, and concentration of each enzyme.

• Temperature
  • MATLAB - Very flexible as it incorporates the Arrhenius law which models the temperature-dependent reaction rate constant. You can input a temperature into an interactive prompt.
  • Spatial Kappa - Flexible. There is no empirical relationship incorporated in the model, however by changing diffusion rates between compartments one could (very imprecisely) simulate changes in temperature. There is a possibility that more precise results could be achieved using the Stokes-Einstein equation:
    
    

    

    T₁ and T₂ denote temperatures 1 and 2, respectively
    D is the diffusion coefficient (cm²/s)
    T is the absolute temperature (°K),
    μ is the dynamic viscosity of the solvent (Pa·s)
    
    (After [http://en.wikipedia.org/wiki/Mass_diffusivity#Temperature_dependence_of_the_diffusion_coefficient Wikipedia])
  • C - Temperature does not exist in the model. It would however be possible to extend it so that a temperature parameter influenced things like enzyme movement speed and probability to cut bonds.

• Enzyme concentration
  • MATLAB - Can easily be changed by inputting a value (in the range of 0-1 g/kg for each enzyme) into an interactive prompt. The flexibility is beneficial especially when investigating optimum operating conditions in the biorefinery.
  • Kappa and Spatial Kappa - It is possible to change the number of enzyme agents by editing a separate file, which affects the relative concentration of enzymes (say, 3 times more of enzyme A than B). However, it would be non-trivial to translate that into an absolute value (e.g. 0.5 g of enzyme per 1kg of solution).
  • C - Similarly to Kappa, this can easily be changed in relative terms.

• Strength of inhibition
  • MATLAB - Incorporates inhibition of enzymes based on glucose and cellobiose concentrations; the strength can be changed. There is also scope for xylose inhibition, but it is set to zero in this model.
  • Kappa and Spatial Kappa - The inhibition rates can be easily changed by editing a file with parameters.
  • C - Incorporates inhibition of exoglucanase by individual cellobiose molecules based on spatial location. Could be extended to include inhibition by glucose; and also to have free glucose taken out of the system after it is made.

• Amount of raw material input
  • MATLAB - An interactive prompt asks the user for an initial amount of cellulose.
  • Kappa and Spatial Kappa - The initial amount of cellulose can be modified by editing a file. Also, in Spatial Kappa we ran experiments with adding more cellulose during the process.
  • C - The amount can be passed as a command-line argument.

Computational cost

The MATLAB, C and Kappa models do their work in relatively short periods of time.

In contrast, the Spatial Kappa model takes a significant amount of time to run (about 30 minutes, depending on the settings of parameters). This is due to the way in which space is represented. In a system with n compartments in d dimensions, a typical rule would be translated into n^d Kappa rules.

Representing reality

The MATLAB model is based on the empirical literature, and so should be the best representation of reality. Units of substrate is grams per kilogram (g/kg) and time is in hours. The kinetic rates are based on experimental data which gives the model some validity, however only within certain time limits.

However, since literature was not available for the synergistic system (with closely linked enzymes) we are considering, we had nothing to base a MATLAB model of synergy on. So, our only MATLAB model is the non-synergistic system.

The C and Spatial Kappa models were capable of comparing a synergistic and a non-synergistic system, but in both cases the model is highly abstract and based only on our understanding of the system due to unavailability of empirical data for dynamics of cellulose, cellobiose and glucose.

Ability to reach steady state

We found that the equations used in MATLAB for deterministic modelling only gave sensible answers when the model parameters remained within certain limits. Outside those limits, results could be physically impossible; e.g. producing negative amounts of cellobiose and so breaking the law of conservation of mass. The deterministic model always had reactants available, i.e. cellulose able for every reaction, ensuring it would never reach zero. A 'stress test' was carried out simulating the model over one hundred thousand hours confirming this. Therefore, within the limits of differential equation based modelling, it is unlikely to reach a mathematical steady state. An engineer considers the system to be in steady state when 99% of the initial amount of cellulose has been degraded, which was found to occur after 8000 hours. However, the 'stress test' revealed (Figure 3) that neither the mathematical nor engineering concept of steady state will be reached for cellobiose and glucose in the MATLAB model.

By contrast, in the C model and Kappa model, cellulose, glucose and cellobiose all reach steady state within a finite period of time. Analysing steady state is important to find out whether a model violates the laws of thermodynamics by accumulating excess mass or energy over the time period of interest. Regrettably, the MATLAB model does.

Conclusions

Although it is hard to compare the different approaches we took and even harder to choose and recommend the best one, our modelling gave us some important insights.

To begin with, we successfully modelled synergy in C and Spatial Kappa. In case of MATLAB, there is still potential to improve the model to show synergy, whereas it would be at least very cumbersome to do the same in plain Kappa.

The MATLAB model should be the one most closely representing real-world levels of reactants in the system. That is due to the fact that the model is built using experimentally adjusted values of constants and informed with known reaction equations. However, given sufficient data, it is also possible to adjust the Kappa / Spatial Kappa models to use different kinetic rates and concentrations of enzymes. It would require major modifications to achieve the same in the C model.