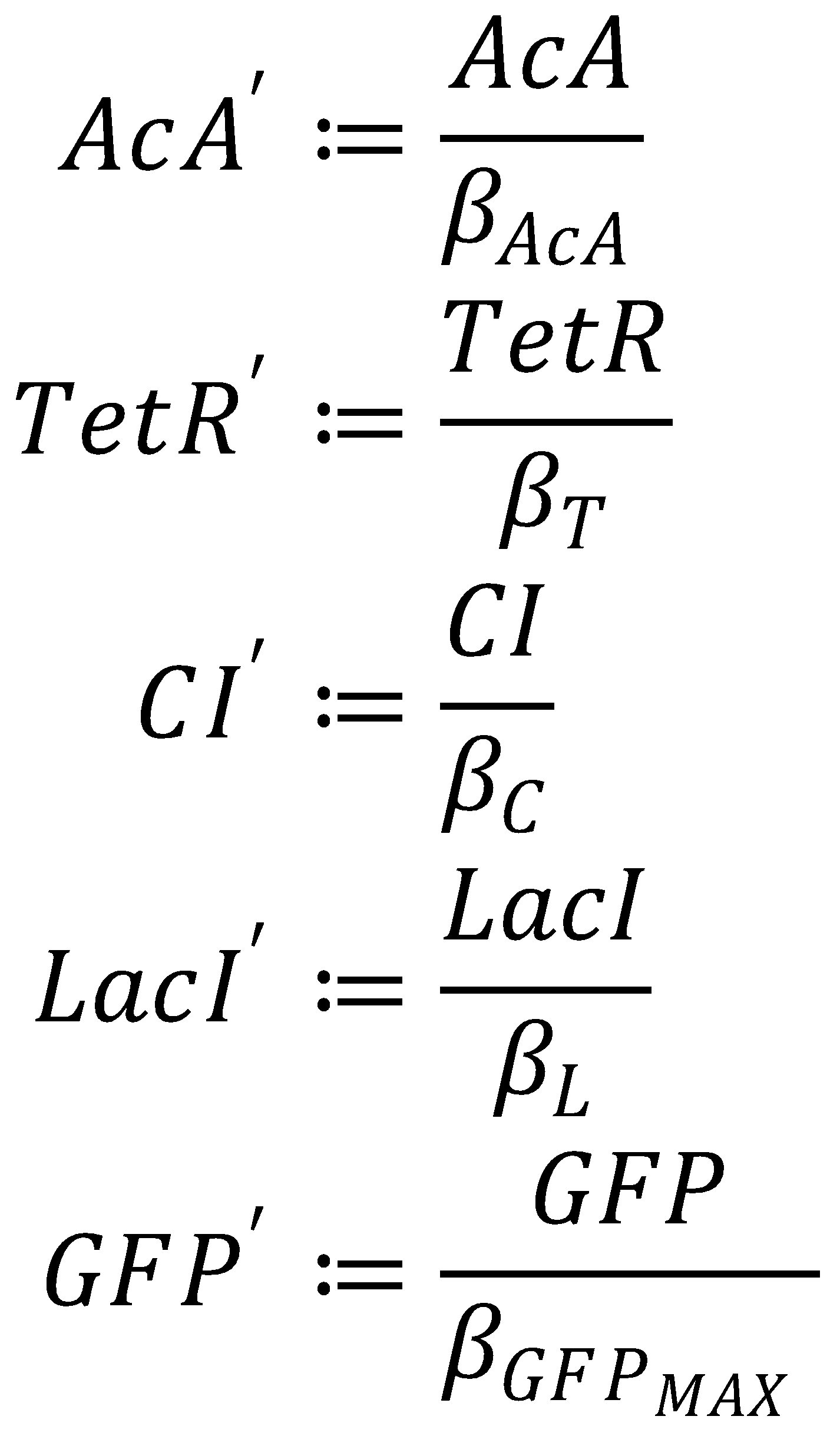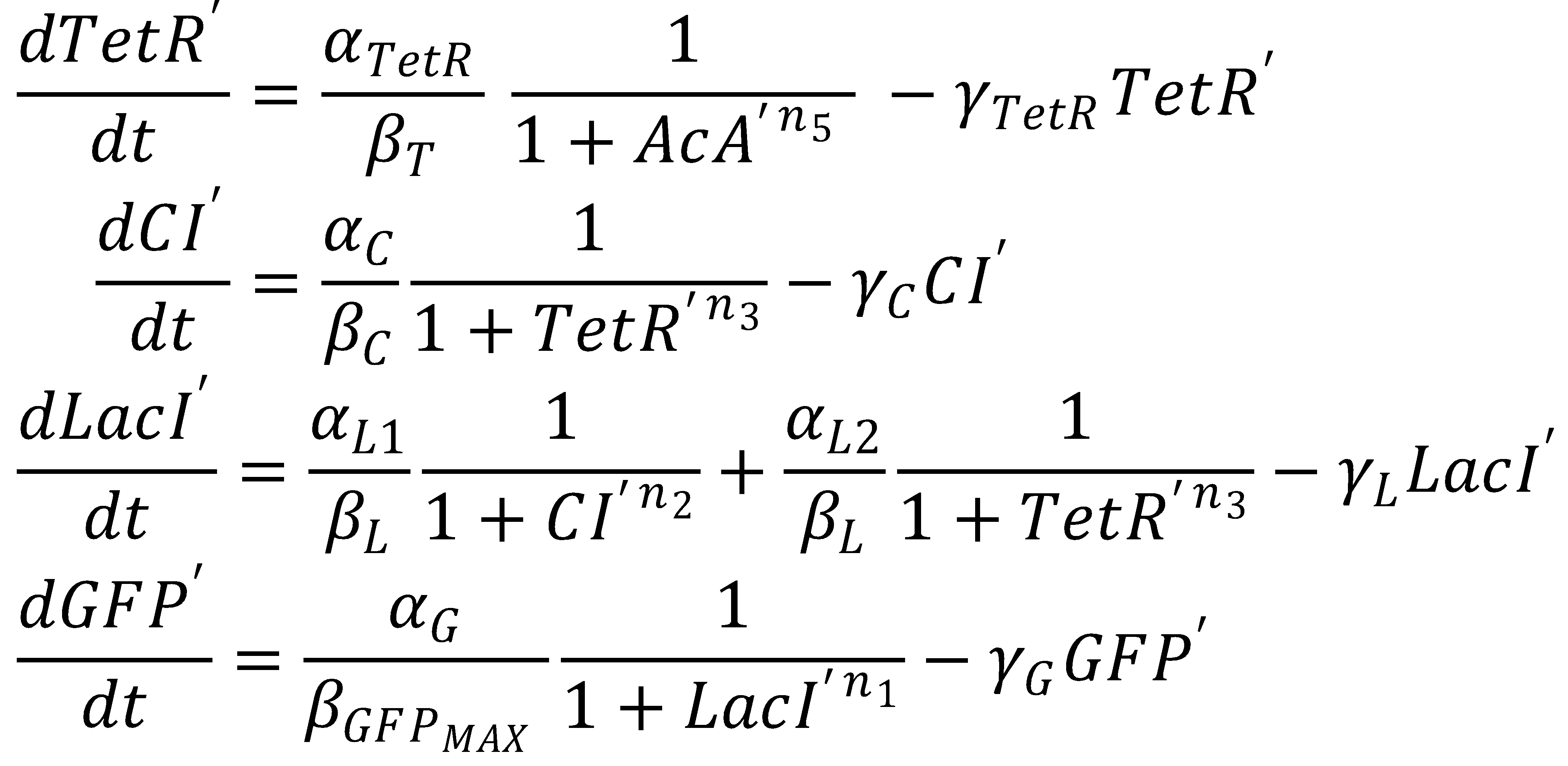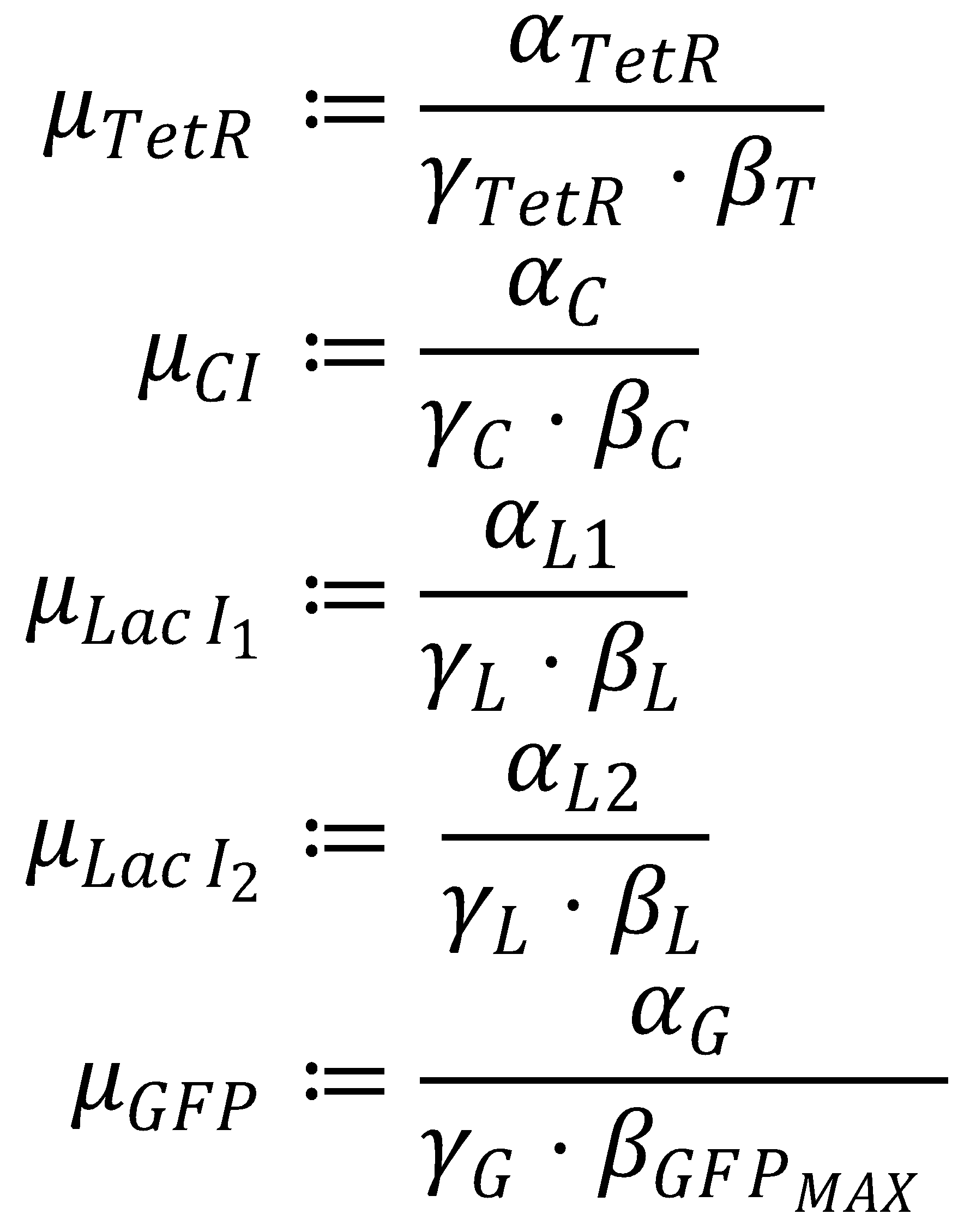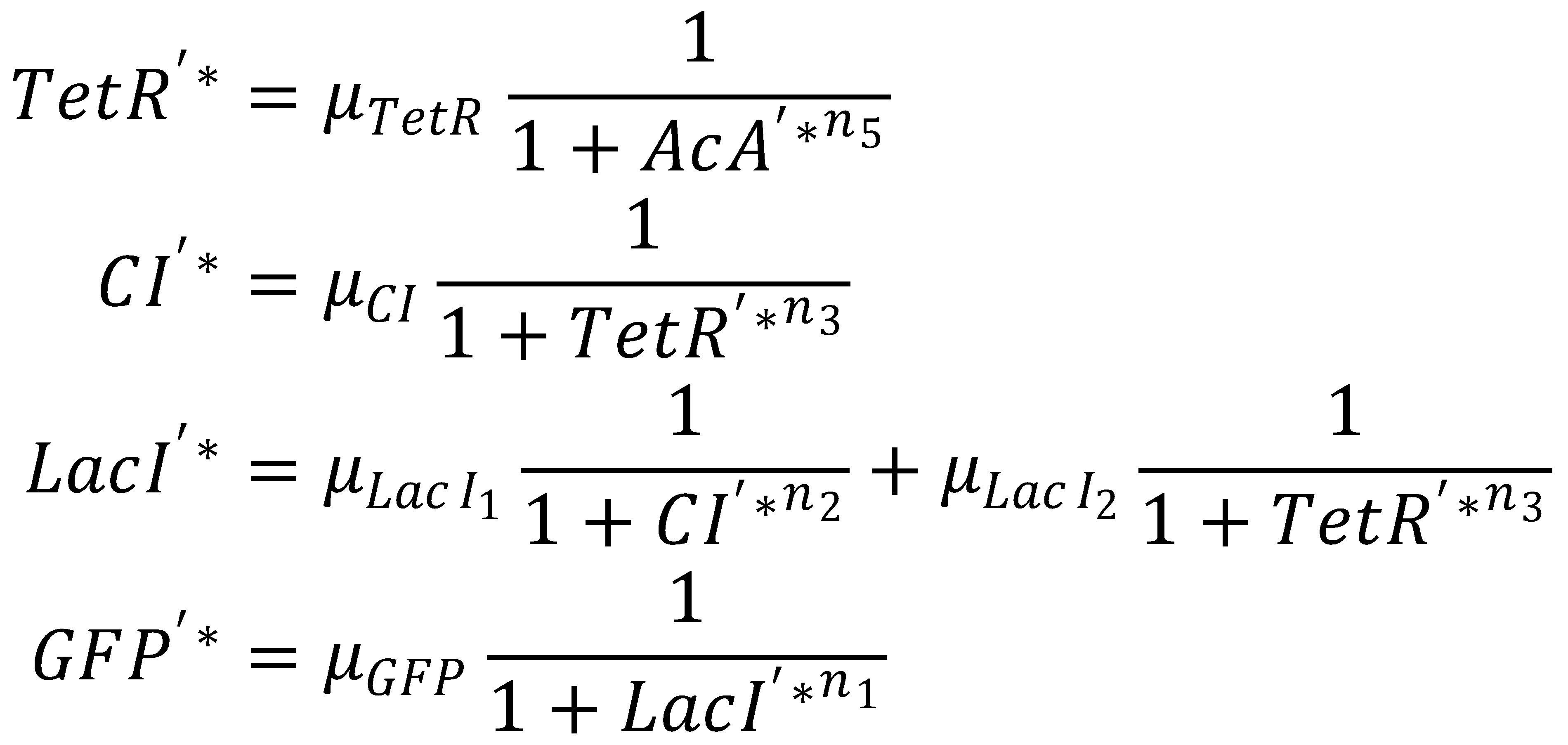Team:ETH Zurich/Modeling/Analytical Approximation
From 2011.igem.org
(→Kolmogorov-Petrovsky-Piskounov Equation) |
(→Kolmogorov-Petrovsky-Piskounov Equation) |
||
| Line 31: | Line 31: | ||
We derived the gradient formation dynamics analytically already in the [[Team:ETH_Zurich/Modeling/Microfluidics#Model|reaction-diffusion model]]. However, there we only solved the resulting partial differential equation numerically. '''Here, we are going to venture forth and give a suitable analytical approximation!''' | We derived the gradient formation dynamics analytically already in the [[Team:ETH_Zurich/Modeling/Microfluidics#Model|reaction-diffusion model]]. However, there we only solved the resulting partial differential equation numerically. '''Here, we are going to venture forth and give a suitable analytical approximation!''' | ||
== Kolmogorov-Petrovsky-Piskounov Equation == | == Kolmogorov-Petrovsky-Piskounov Equation == | ||
| - | [[File:ETH-AcAl-Reaction-Diffusion.png|317px|center|thumb|General partial differential equation for an acetaldehyde reaction-diffusion system. '''D(AcAl(x,z),z)''' is the diffusive term, '''R(AcAl(x,z))''' is the uniform (independent of the spatial z coordinate) reaction term.]] | + | In mathematics, the problem posed by general reaction-diffusion systems form is known as the '''Kolmogorov-Petrovsky-Piskounov Equation'''. In the case of acetaldehyde as diffusing and reacting molecule, the equation has the following general structure: |
| - | + | [[File:ETH-AcAl-Reaction-Diffusion.png|317px|center|thumb|General Kolmogorov-Petrovsky-Piskounov partial differential equation for an acetaldehyde reaction-diffusion system. '''D(AcAl(x,z),z)''' is the diffusive term, '''R(AcAl(x,z))''' is the uniform (independent of the spatial z coordinate) reaction term.]] | |
== Dead Zone Concept == | == Dead Zone Concept == | ||
Revision as of 18:12, 27 October 2011
Analytical Approximation
GFP Band: Dimensionless Model
1. Dimensionless Species
We nondimensionalized all species occurring in the equations for the GFP band circuit.
2. Dimensionless Equations
The dimensionless equations for the dynamics of the band-generating system then read
3. Steady State
4. Dimensionless Groupings
The equation system can be simplified by introducing the following dimensionless groupings:
This yields the final equations for steady state:
Gradient Approximation
We derived the gradient formation dynamics analytically already in the reaction-diffusion model. However, there we only solved the resulting partial differential equation numerically. Here, we are going to venture forth and give a suitable analytical approximation!
Kolmogorov-Petrovsky-Piskounov Equation
In mathematics, the problem posed by general reaction-diffusion systems form is known as the Kolmogorov-Petrovsky-Piskounov Equation. In the case of acetaldehyde as diffusing and reacting molecule, the equation has the following general structure:
Dead Zone Concept
Analytical Solution
References
 "
"