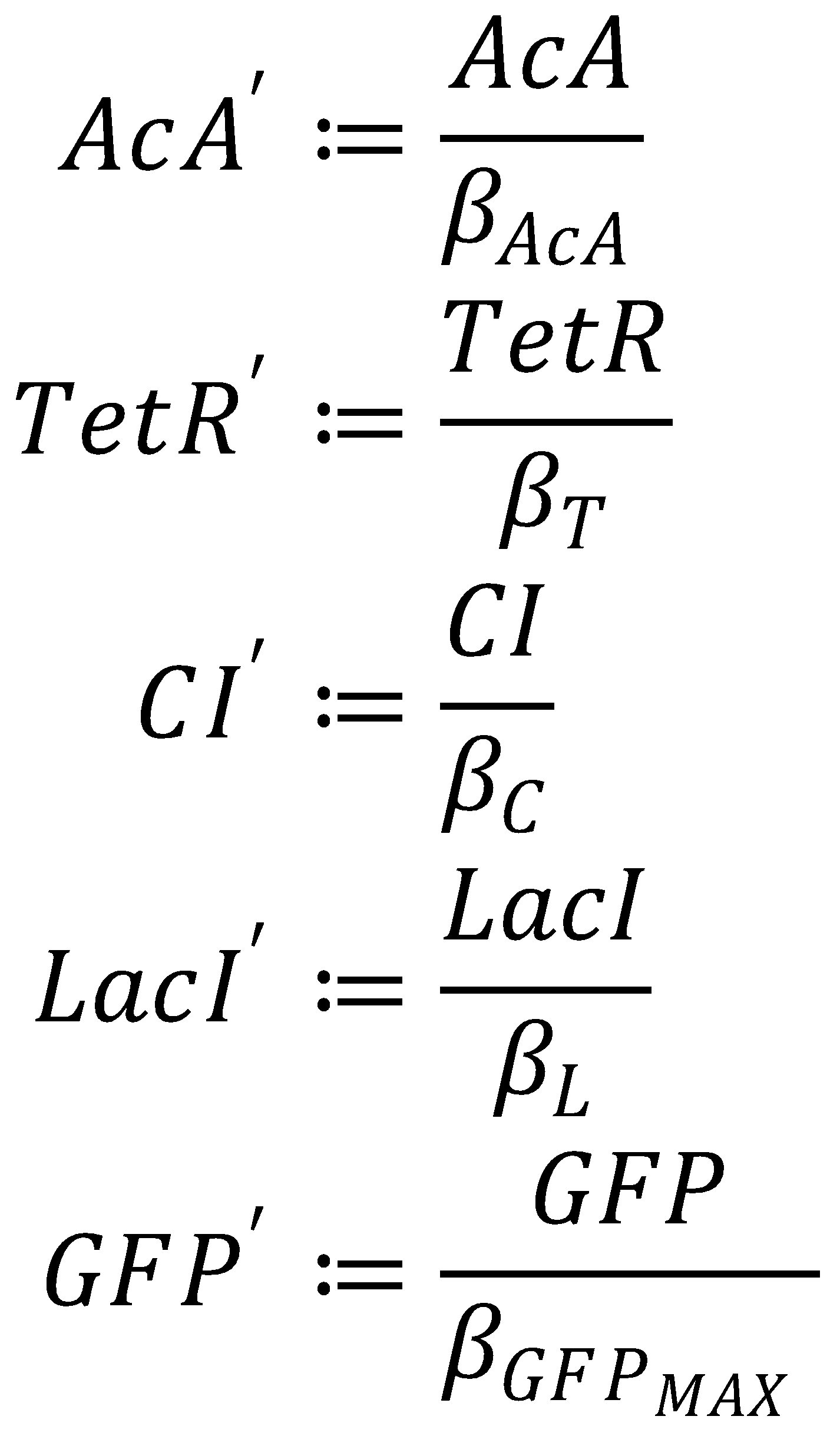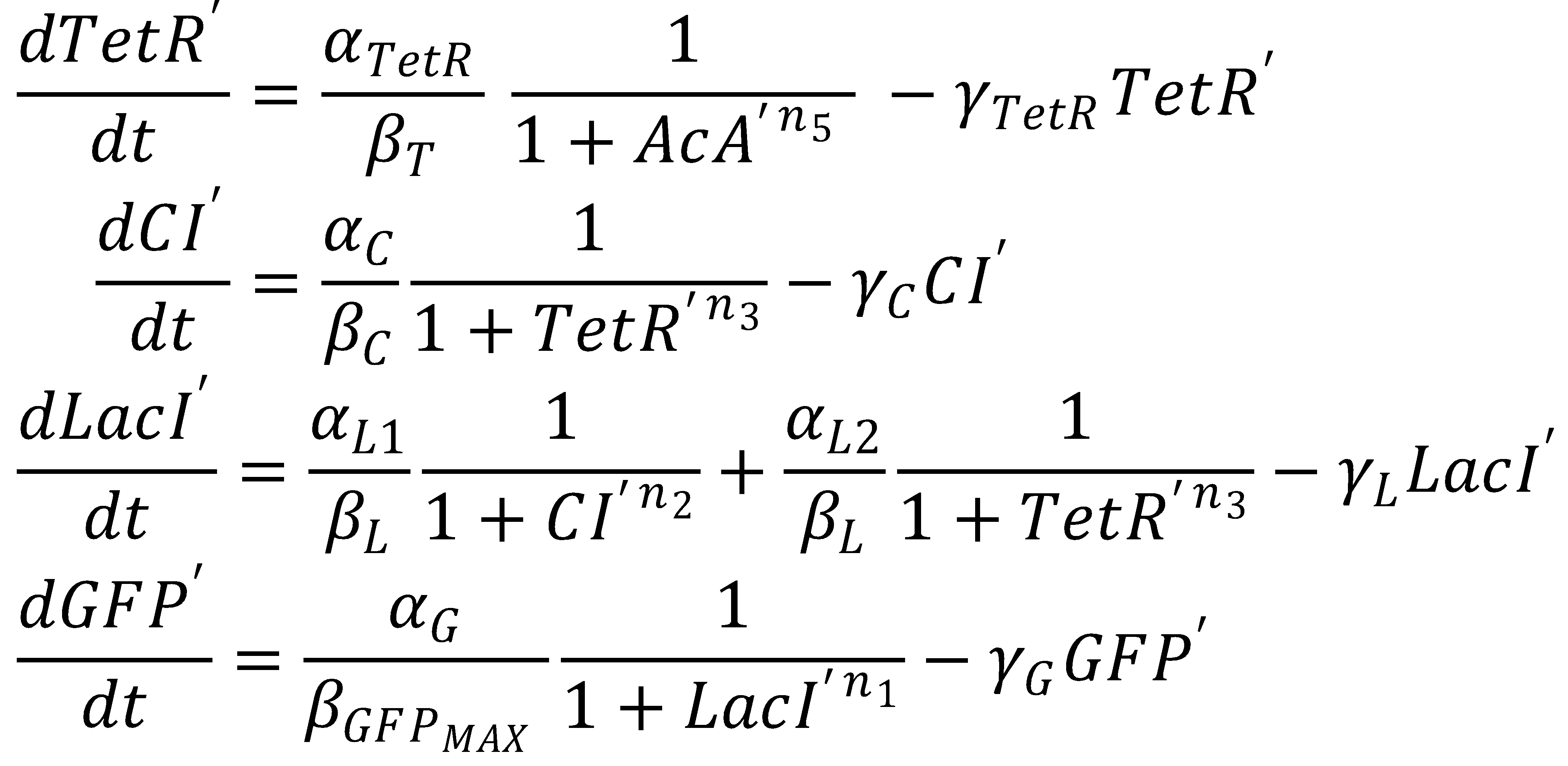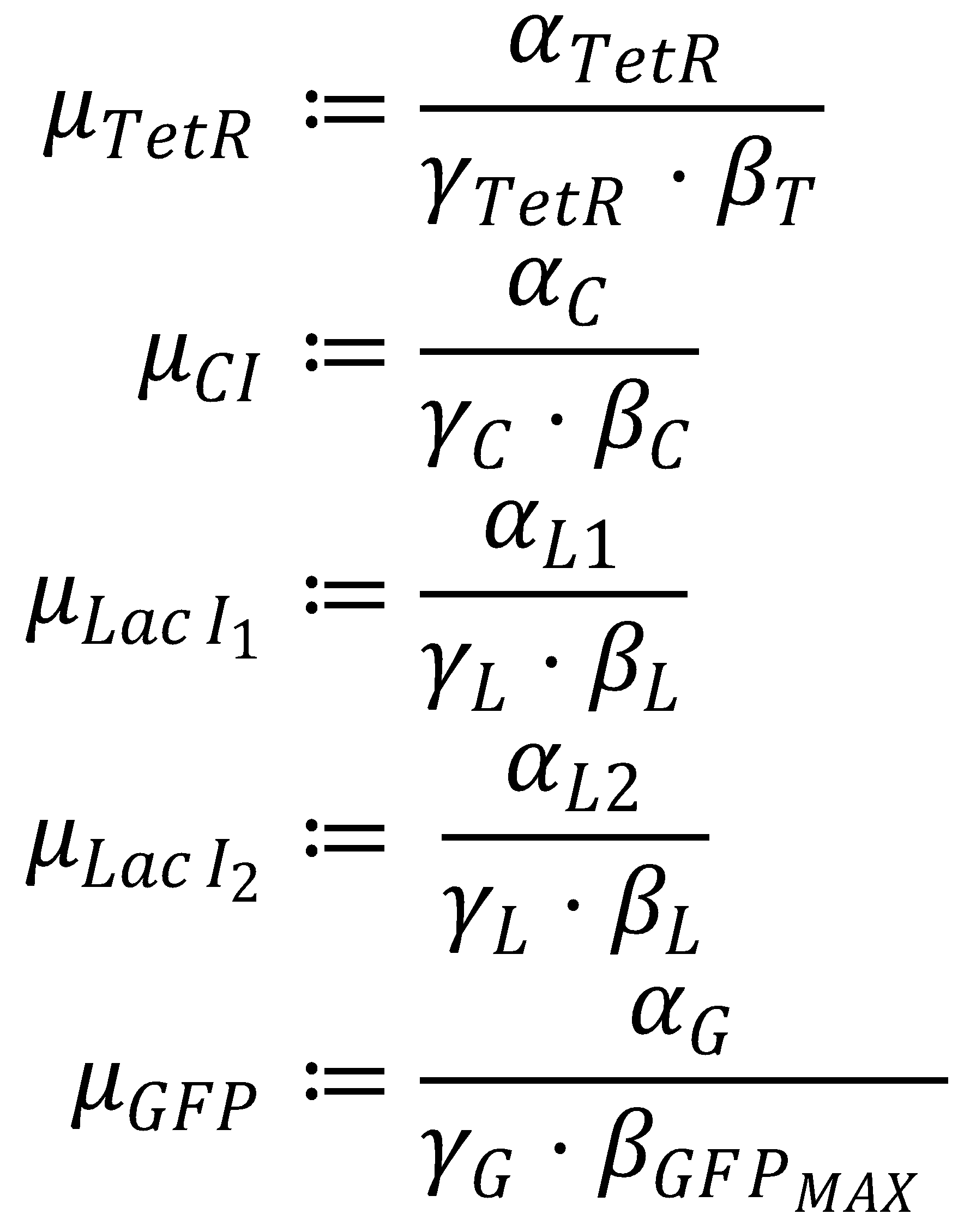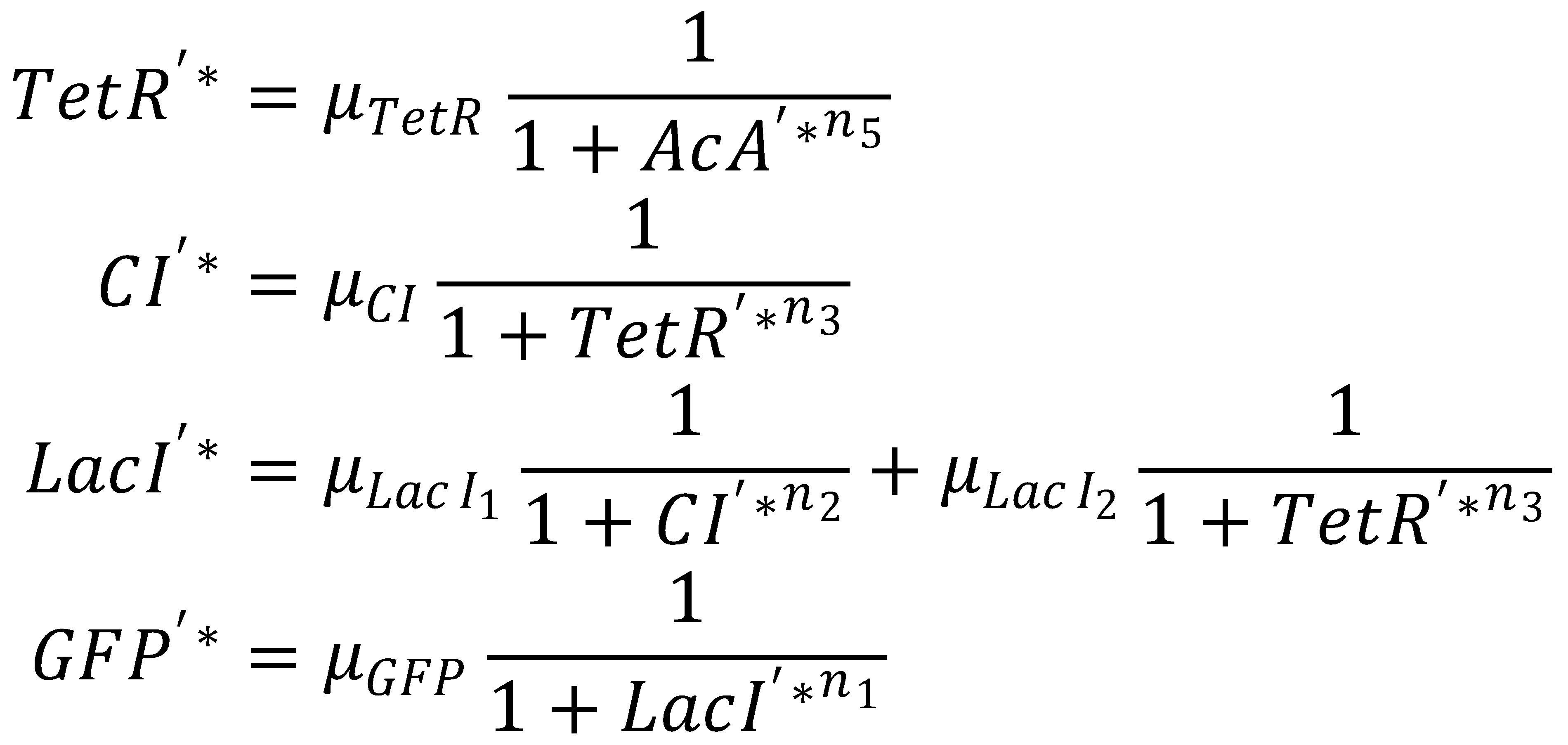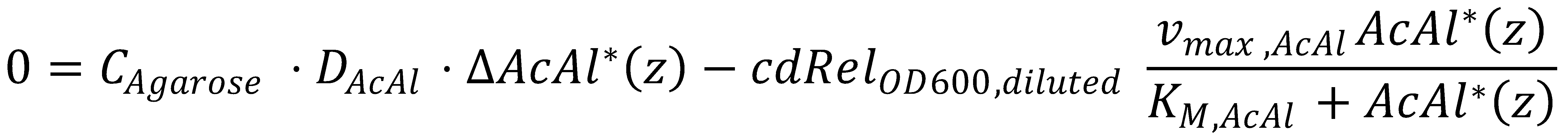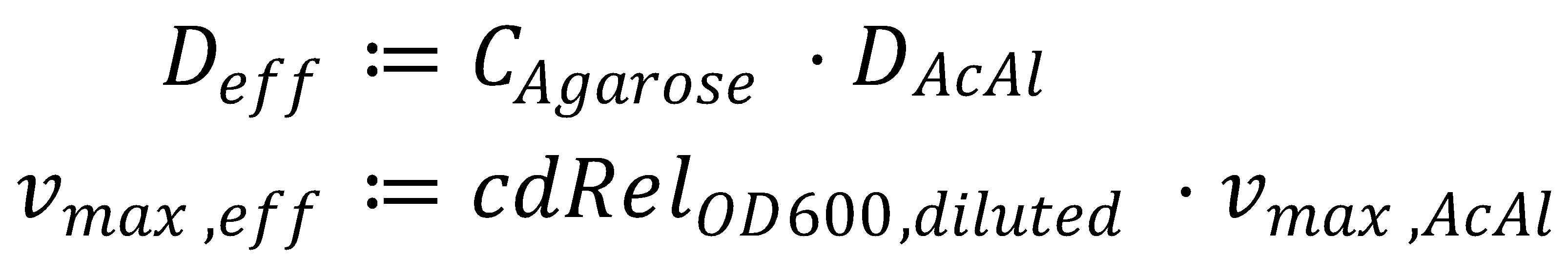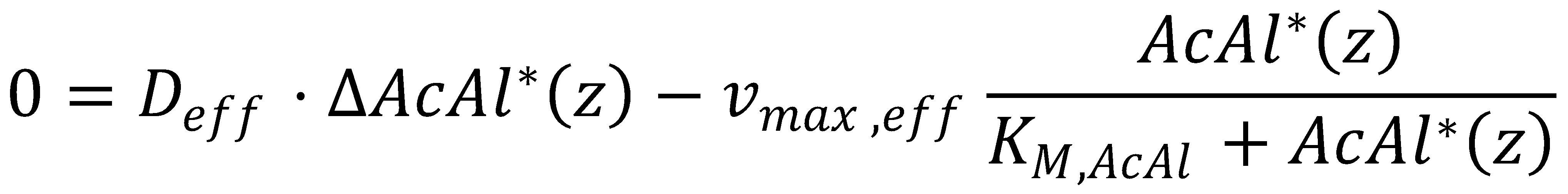Analytical Approximation

GFP Band: Dimensionless Model

1. Dimensionless Species

We nondimensionalized all species occurring in the equations for the GFP band circuit.

2. Dimensionless Equations

The dimensionless equations for the dynamics of the band-generating system then read

3. Steady State

4. Dimensionless Groupings

The equation system can be simplified by introducing the following dimensionless groupings:

This yields the final equations for steady state:

Steady State Gradient Approximation

We derived the gradient formation dynamics analytically already in the reaction-diffusion model. However, there we only solved the resulting partial differential equation numerically. Here, we are going to venture forth and give a suitable analytical approximation!

Kolmogorov-Petrovsky-Piskounov Equation

In mathematics, the problem posed by general reaction-diffusion systems form is known as the Kolmogorov-Petrovsky-Piskounov Equation. In the case of acetaldehyde as diffusing and reacting molecule, the equation has the following general structure:

General Kolmogorov-Petrovsky-Piskounov partial differential equation for an acetaldehyde-based reaction-diffusion system. D(AcAl(x,z),z) is the diffusive term, R(AcAl(x,z)) is the uniform (independent of the spatial z coordinate) reaction term.

Kolmogorov-Petrovsky-Piskounov partial differential equation for our system, as derived in the reaction-diffusion model for acetaldehyde.

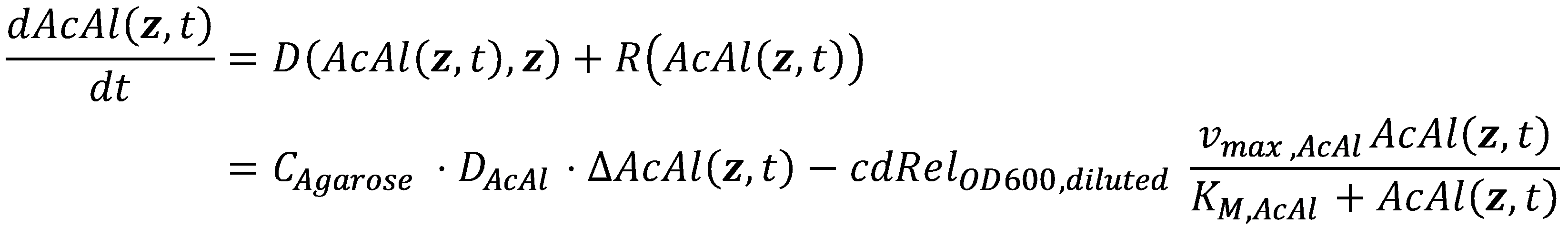
Boundary Conditions

For the analytical approximation of the acetaldehyde gradient, we only consider the boundary condition that the concentration at the reservoir (located at z = 0) stays constant:

[http://en.wikipedia.org/wiki/Dirichlet_boundary_condition Dirichlet Boundary Condition] for the concentration of acetaldehyde at the reservoir

This is in contrast to the full model, where we enforce that no diffusion occurs through the opening at the side of the channel which is closed and not connected to the reservoir. However, we will see that for our circuit, this assumption is valid as long as we are inside the detection range of our circuit, which is the case that we are interested in. In the end, we can also detect if we go out of detection range in the analytical model and make sure this assumption holds.

Solution at Steady State

At steady state, we have to solve the KPP equation for the time derivative set to zero, i.e.

Steady-State Kolmogorov-Petrovsky-Piskounov (KPP) Equation

Before we get started with solving the actual equation, we simplify it by gathering all the parameters we can:

Simplified parameters

Simplified Steady-State Kolmogorov-Petrovsky-Piskounov (KPP) Equation

Dead Zone Concept

Analytical Solution

References

http://www.ncbi.nlm.nih.gov/pubmed/16209545