Team:USTC-Software/parameter
From 2011.igem.org
 USTC-Software
USTC-Software
Parameter ananlysis(Design evaluation)
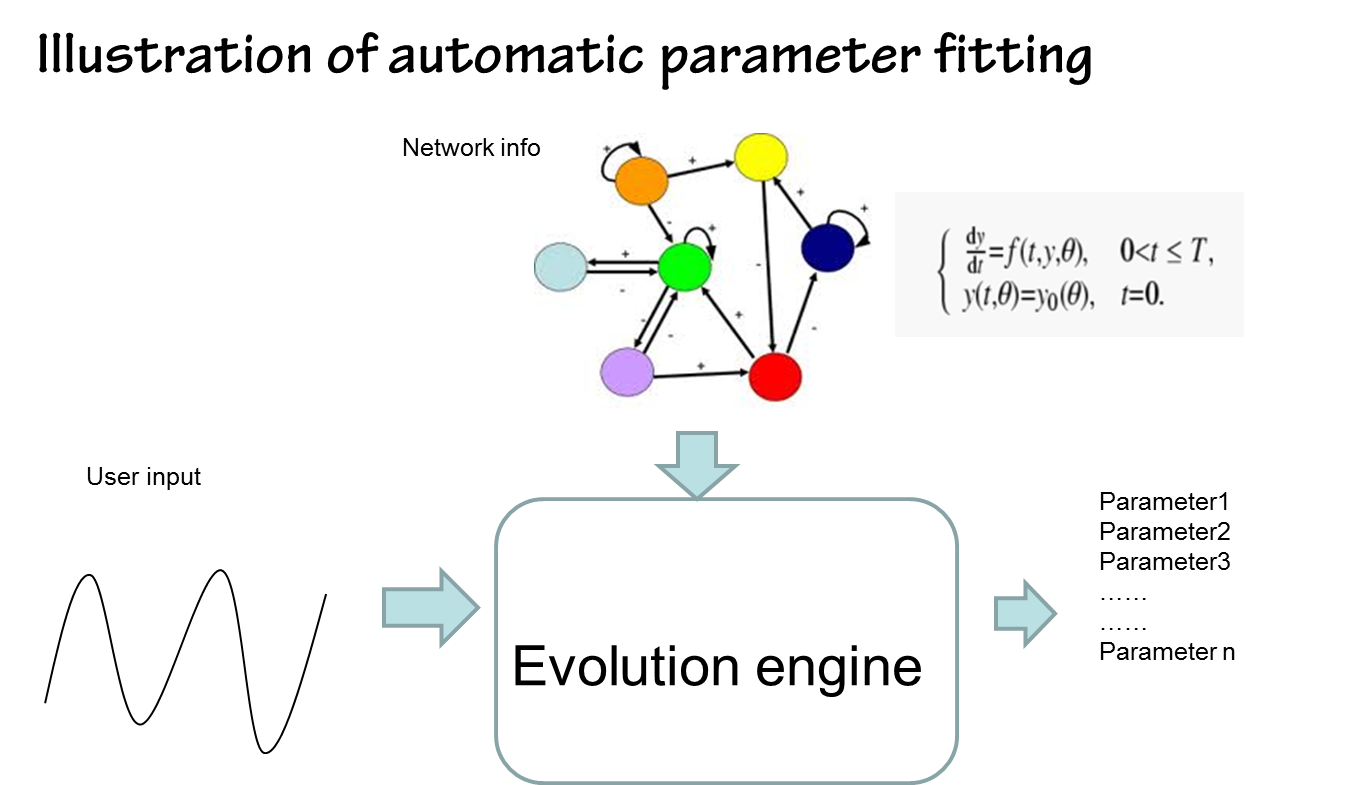
Part1 Automatic Parameter fitting:
1.1 Background
In electronics, You don't have to worry about the parameter problem with each part, circuit design softwares can help the user to easiliy fetch the standardized circuit part with well defined external response parameters from a device library.
Once a circuit is constructed, a mathematical model is formed with all the parameter defined and you only need to simulate. When put into practice, you just need to fine tune the behavoior with a rheostat
However, in synthetic biology, Some parameters of the parts haven’t been measured yet. Some parameters with quantitative mesured values, which are highly context dependent, can hardly be transfered across different hosts.
So when a gene circuit is contructed, the mathematical model associated with it is left with most parameters undefined. If you want to achieve a certain behaviour, you have to adjust a set of parameter values and run the simulation to check if it works.
Usually, you have to fill in a form of specified parameter values manually many times until it works
1.2 The advantage of automatic parameter fitting compared with manual parameter fitting
- Network generated by rule based modeling is ordinarily large
If it’s a big network with too many parameters undefined, it would get the user exhausted adjusting all the empty parameters by hand according to his/her experience and web resource.
- Compared to manually parameter adjustment, in silicon auto parameter adjustment is more convenient.It gives an estimation of the interest parameter value according to wet lab data, thus free the user from spending too much time on estimating a good parameter.
1.3 examples
We adopted a demo from a Tinkercell tutorial website on implementing a simple repressilator. After the network is generated by hand, the parameters are left behind to the user to adjust by themselves. But as you can see from the following figures, the process is tough and time consuming. (more snapshots of the process of manual parameter fitting are eliminated )
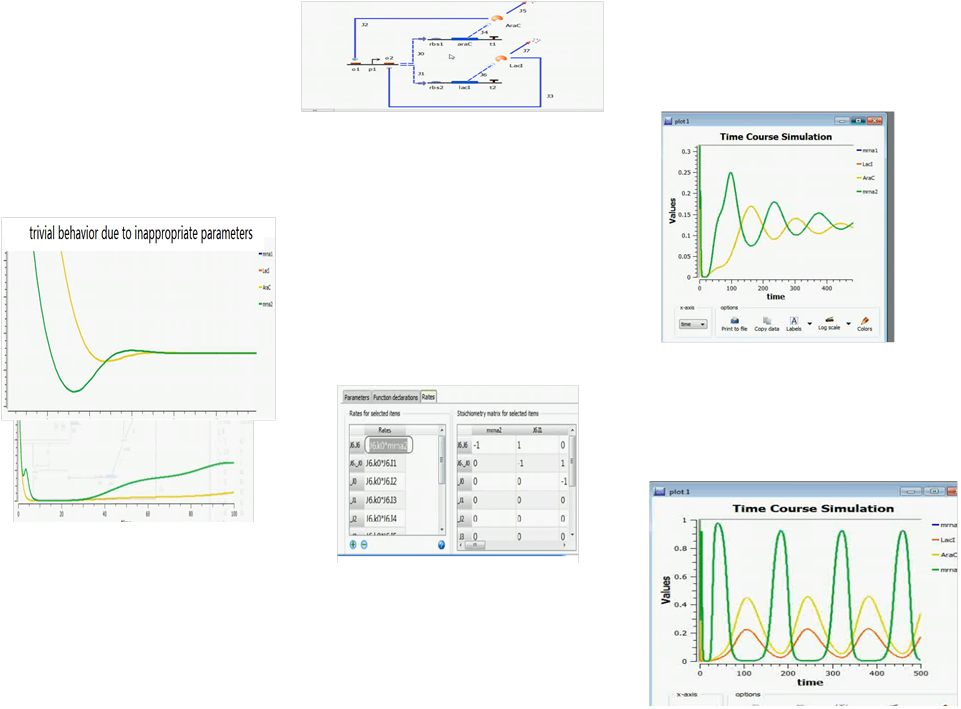
The figure above show a difficult parameter adjustment process by hand.
By contrast, parameters estimated by our approach in silicon can be done in a timely fashion. It’s fast and convenient(see figure below)
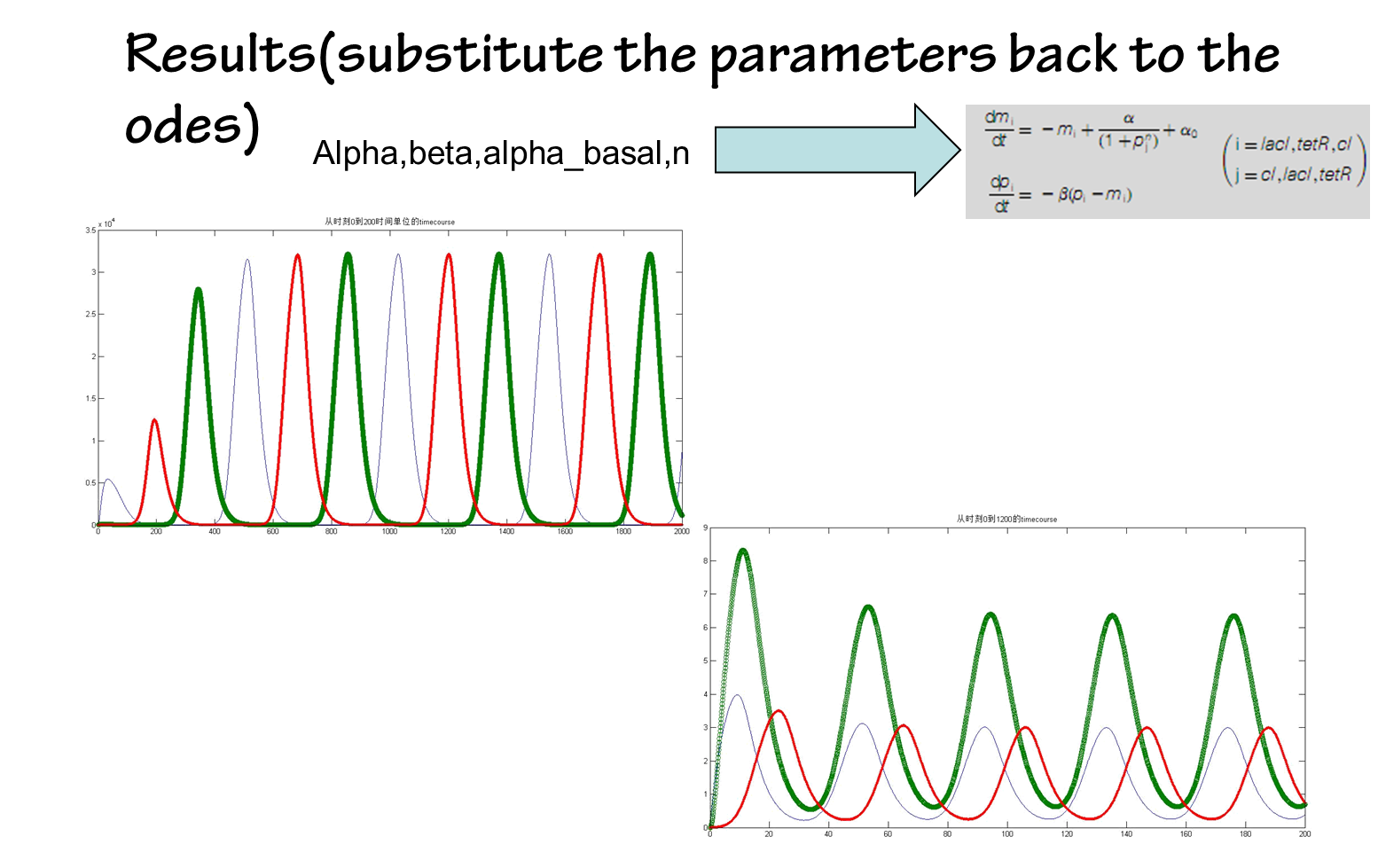
 the results are shown below(we choose the classical repressilator as an example)
the results are shown below(we choose the classical repressilator as an example)
Part2 Workability evaluation:
2.1 background
The workability of a design for a desired behaviour have to be evaluatedComputer descriptions of biological mechanisms are by necessity,very simplified.The biology system is so complex that current mathematical description is far from accurate
Parameters of biological parts are context dependent and some may vary drastically when host cell or environment change.Noise come from various sources and can drastically influence the performance of a circuit
When a mathematical model is given, only limited parameter regions will promote a desired behavior.Things that can be implemented through ode parameter adjustment might not necessarily be observed in real experiment.If the parameter range is "slim" at the working region, then most probably the desired phenomena will never be observed in wet experiment.
Problem of evaluating whether a design will work
The dimension of the parameter space can be high, maybe tens of dintinct parameters or much more, and the formula of the model are highly unlinear, so it's hard to figure out the workable regions analytically.
2.2 Our ideas about how to evaluate a design
Rather than to see how well the system can retain it's desired output against parameter variation, which is the most common defination of robustness. We focus our view on when the desired behavior is maintained, to what extent can the system bear parameter variation.
We sovle this problem by random sampling in the multi-dimension parameter space. This can be viewed as figuring out the profile of the parameter space through the samples set
So it's a problem of interpreting the data acquired by random sampling. fitness of the parameters
With a specified parameter set(p1,p2,…pn), one can run the ode simulation of the mathematical model associated with the gene circuit, to see whether the output behaviour make sense. To make a comparison between the output behavior of the simulation and the desired outcome, we introduce the fitness criteria, which can be done by computing cross correlation or absolute distance.
Firstly, with a predefined cutoff fitness value, Monte Carlo sampling is applied to collect enough parameter samples, in this process, only those with a fitness above the predefined value will be reserved, thus forming a large data set of workable parameters. In this random sampling process, when a new parameter configuration's fitness exceed the fitness of the old one, the new parameter configuration is preserved. When the fitness of the new parameter confituration is lower than the old one ,there is a probality of accepting that.Thus trying to make a more unbiased sampling.
This process can be run at different initial points.
The next step is to use the generated data to depict the profile of the workable region.
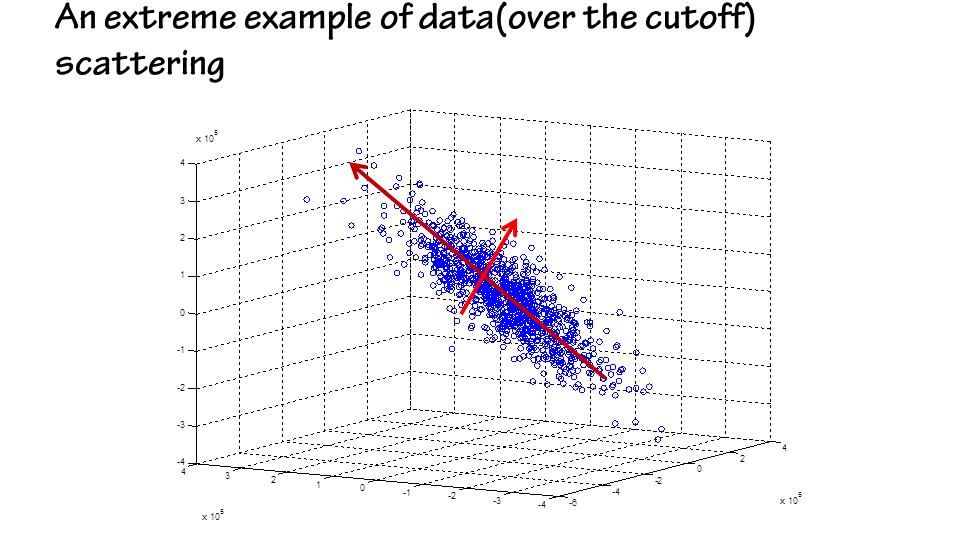
An additional benefit of PCA analysis is the multivariate sensitivity information it can find.
Gene circuits are usually robust in a single dimension of the parameter space,for variations in one direction will be compensated by other directions.
The new axis with the smallest variation correspond to the most sensitive direction of parameter variation.
If we get the most sensitive parameter direction, we probably know what to do to refine a circuit to quick tune it to a desired behavior or just try to keep that most sensitive parameter as constant as possible.
So the less principal component of the PCA result correspond to the most sensitive parameter direction, which should be put attention.
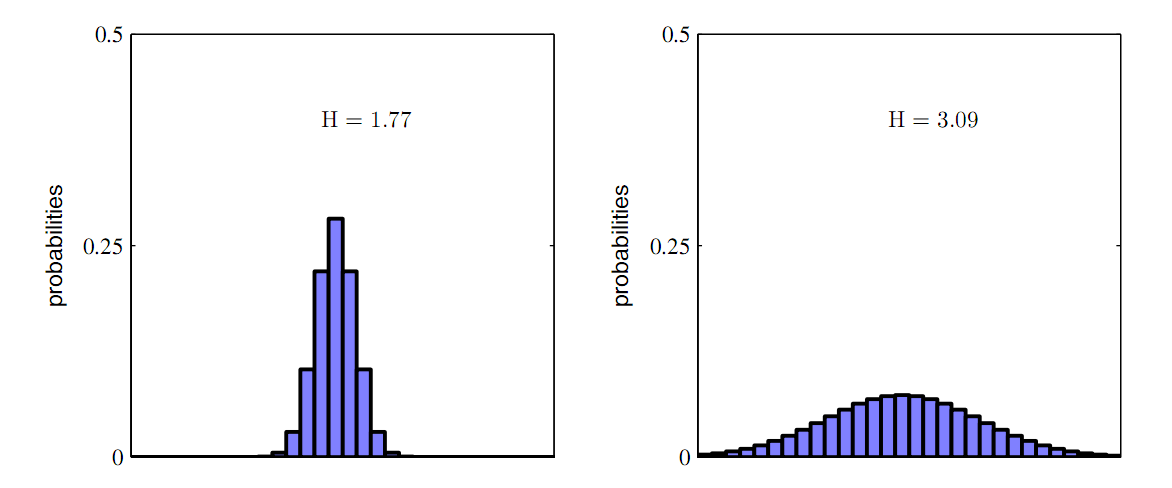
As you can see from the one dimensional case of the two figures above, the more broad distribution of parameters correspond to a bigger entropy. Thus, we can use entropy to depict the "broadness" of the the distribution of parameters. The more broad the distribution is, the more robust is the system, and the easier is it to achieve in real wet experiment. In other words, the gene circuit has a lot of parameter choices when in a changing environment.
The entropy method can be easily expanded to multi-dimensional case.
The parameter space can be divided to form a lattice, with each grid representing a state of the parameter sample. a simple formula H=-Ni/N*logNi/N, where Ni representing the number of dots lying inside the grid representing state i and N the total number of dots in the parameter space.
For multivariate Gaussian distribution, the entropy directly correspond to its covariance matrix.
comparison with some existed tools
Some existed robustness and sensitivity tools require the user to predefine a set of reference parameters and variate parameters to see the difference.
However, it may be time consuming for user to specify an accurate value to each parameter. And for novice to synthetic biology, this can hardly be done. Our approach only require the user to give a range to each parameter which is more convenient
Some existed tools also require the user to specify the way the perturbations are operated. Our approach conduct a weighted random sampling approach to variate the paramters.
For some existed tools, if you want to compare the robustness of two designs, the output functions should be the same.
Our approach's result is only a number, which is more general, it just indicate how broad is the workable parameter region.
To put in one, most robustness analysis are based on sensitivities, which is mesurement of how well the circuit can retain a desired behavior against parameter variation , while our approach aims at when the desired behaviour is maintained, to what extent can the parameters be varied, which is a counterpart to other methods
Particle swarm optimization (PSO) is a population based stochastic optimization technique developed by Dr. Eberhart and Dr. Kennedy in 1995,
inspired by social behavior of bird flocking or fish schooling. The particle swarm concept originated as a simulation of simplified social system.
The original intent was to graphically simulate the choreography of bird of a bird block or fish school.
However, it was found that particle swarm model can be used as an optimizer. Each particle keeps track of its coordinates in the problem space which are associated with the best solution (fitness) it has achieved so far. (The fitness value is also stored.)
This value is called pbest. Another "best" value that is tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the neighbors of the particle.
This location is called lbest. when a particle takes all the population as its topological neighbors, the best value is a global best and is called gbest. The particle swarm optimization concept consists of, at each time step, changing the velocity of (accelerating) each particle toward its pbest and lbest locations (local version of PSO).
Acceleration is weighted by a random term, with separate random numbers being generated for acceleration toward pbest and lbest locations. PSO has been successfully applied in many research and application areas.
It is demonstrated that PSO gets better results in a faster, cheaper way compared with other methods. Simulated annealing (SA) is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities).
For certain problems, simulated annealing may be more efficient than exhaustive enumeration — provided that the goal is merely to find an acceptably good solution in a fixed amount of time, rather than the best possible solution. In the simulated annealing (SA) method, each point s of the search space is analogous to a state of some physical system, and the function E(s) to be minimized is analogous to the internal energy of the system in that state.
The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy. At each step, the SA heuristic considers some neighbouring state s' of the current state s, and probabilistically decides between moving the system to state s' or staying in state s. These probabilities ultimately lead the system to move to states of lower energy.
Typically this step is repeated until the system reaches a state that is good enough for the application, or until a given computation budget has been exhausted. The neighbours of a state are new states of the problem that are produced after altering the given state in some particular way. For example, in the traveling salesman problem, each state is typically defined as a particular permutation of the cities to be visited. The neighbours of some particular permutation are the permutations that are produced for example by interchanging a pair of adjacent cities.
The action taken to alter the solution in order to find neighbouring solutions is called "move" and different "moves" give different neighbours. These moves usually result in minimal alterations of the solution, as the previous example depicts, in order to help an algorithm to optimize the solution to the maximum extent and also to retain the already optimum parts of the solution and affect only the suboptimum parts.
In the previous example, the parts of the solution are the parts of the tour. The probability of making the transition from the current state s to a candidate new state s' is specified by an acceptance probability function P(e,e',T), that depends on the energies e = E(s) and e' = E(s') of the two states, and on a global time-varying parameter T called the temperature. States with a smaller energy are better than those with a greater energy. The probability function P must be positive even when e' is greater than e.
This feature prevents the method from becoming stuck at a local minimum that is worse than the global one. Below is an aflow chart that demonstrates the whole process:Part3 Evolution Algorithm introduction
Particle swarm optimization (PSO) Algorithm
History
Algorithm introduction

Application
Simulated Annealing(SA) Algorithm
Principle of the algorithm
Steps
State transition
Probability function of the state transition


 "
"
