Team:Washington/Alkanes/Future/Modeling
From 2011.igem.org
Emily Yang (Talk | contribs) (→Appendix) |
Emily Yang (Talk | contribs) (→Appendix) |
||
| Line 30: | Line 30: | ||
1. E. Coli metabolic network [[Media: Ec_iJR904_GlcMM.txt]] | 1. E. Coli metabolic network [[Media: Ec_iJR904_GlcMM.txt]] | ||
| - | |||
2. MATLAB code for FBA [[Media: Matlab_Script.m]] | 2. MATLAB code for FBA [[Media: Matlab_Script.m]] | ||
Revision as of 05:54, 28 October 2011
Background
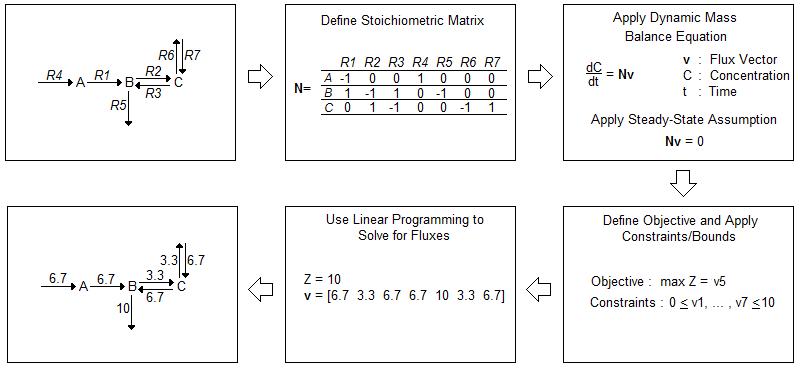
While in vivo analysis is invaluable, computational modeling can help direct experiments in a way that conserves time and resources. Current in silico models often rely on flux balance analysis (FBA) as an optimization algorithm. FBA provides a method for tracking fluxes within a biological system and “analyz[ing] biological networks in a quantitative manner” [1]. A flow chart of FBA methodology is depicted in Figure 1 [1].
FBA begins with the construction of an often complex biological network. After accounting for all fluxes within a system, FBA involves the construction of a stoichiometric matrix (N) where each column corresponds to a chemical reaction within the system and each row a molecular species. The matrix is then multiplied by a vector of internal and exchange fluxes (v), shown in Equation 1.
dx/dt = Nv {1}
Since FBA is a static model, the steady-state assumption, shown in Equation 2, applies. The overall equation simplifies to Equation 3.
dx/dt = 0 {2}
Nv = 0 {3}
Constraints are applied to the stoichiometric matrix to limit the number of possible solutions. These constraints often depend on the uptake rate and availability of nutrients within the media in which the cells are growing. A cell cannot take in a substrate if it is not available within its environment. After determining the constraints, an objective is defined, such as maximized protein production or maximized cell growth. Then, the fluxes that maximize the objective are mathematically calculated [1].
Methods
References
Appendix
1. E. Coli metabolic network Media: Ec_iJR904_GlcMM.txt 2. MATLAB code for FBA Media: Matlab_Script.m
 "
"