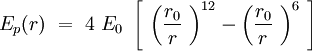Membrane tension calculation

Once the nanotube connexion between two bacteria is established ( click here to see the details on the nanotube formation ).

Motivation

Let's evaluate the constraints that impact the membrane. As it is a Gram positive bacteria, the external sugar envelope imposes the shape of the bacteria. On the other hand, the osmotic pressure is pushing the membrane against the sugar wall. We assume that on the time scale of our model, the total number of phospholipids inside the membrane is fixed, but the density of phospholipids can fluctuate depending on the phospholipid production. So we can pretend that our system is evolving through a series of quasi-equilibrium states.


Fig. 2: If there is an excess of phospholipids, the membrane is being compressed	Fig. 3: If there are not enough phospholipids, the membrane is being extended

The membrane tension is caused by interaction between phospholipids on the surface of bacteria. Closer the phospholipids are to each other, more the membrane is tense.

Can we describe the interaction between two phospholipids in the membrane? The question is complicated, but we will demonstrate that by describing properly the phospholipid, as it is reasonable to fit a Lennard-Jones potential energy to this interaction. Since the speed of conformational equilibration of phospholipid is way faster than the sliding of neighboring phospholipids we can consider phospholipids as cylinders (see the Fig. 4). To make things even simpler we decided to approximate these cylinders as points(see the Fig. 5).

</html>


Fig. 3: Chemical structure of a phospholipid	Fig. 4: Cylindrical approximation of Israelachvili for a phospholipid	Fig. 5: Our approximation

As we can see the modelers go always straight to the point :)

Speaking in terms of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a steric repulsion keeps the molecules apart, and the hydrophobic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients.

The membrane tension calculation

Some hypotheses used :

We deal with a system under fixed temperature, so we can reason in canonical ensemble terminology

Every bacterium in this model has a perfectly spherical form, so each phospholipid on it has 4 degrees of freedom (2 coordinates, 2 momentums per phospholipid)

We will consider phosphlipids equally distributed on the membrane and only the initial density of this distribution can change

Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the whole sphere surface per one phospholipid :

The caracteristic distance between two neighbor phospholipids on the membrane can be written like this :

where N is the number of phospholipids on the membrane. From this moment on we will work in canonical ensemble. The temperature is fixed and so is the number of particles in the system N. We also consider that the phospholipids can move only on the sphere surface that means that we will study the evolution of our system in 2N dimentional phase space. The partition function will look like :

Using statistical physics approach, we can say that the phase space has 4N dimensions: two dimensions of impulsion and two dimensions of coordinate for each particle (N is the number of particles in the system).

where the Hamiltonian is :