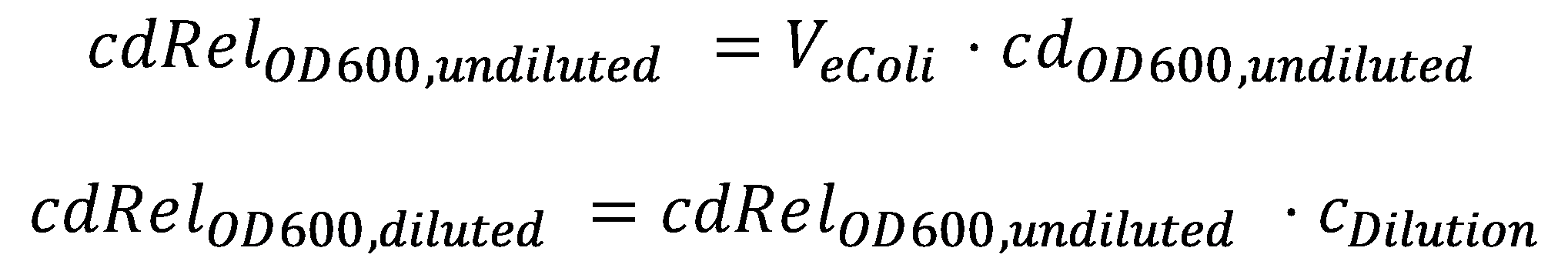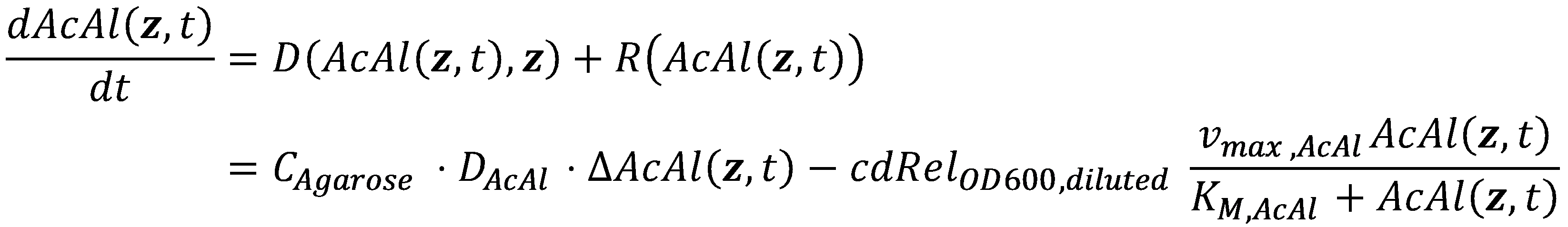Diffusion Model

In our first spatiotemporal model, we wanted to find out if a toxic molecule gradient would be formed at all. The idea was to generate it as an equilibrium of toxic molecule diffusion out of the reservoir into our channel and toxic molecule degradation by the cells in it. In order to answer this question, we modeled a spatiotemporal reaction-diffusion system in 3D with COMSOL Multiphysics.

Overview

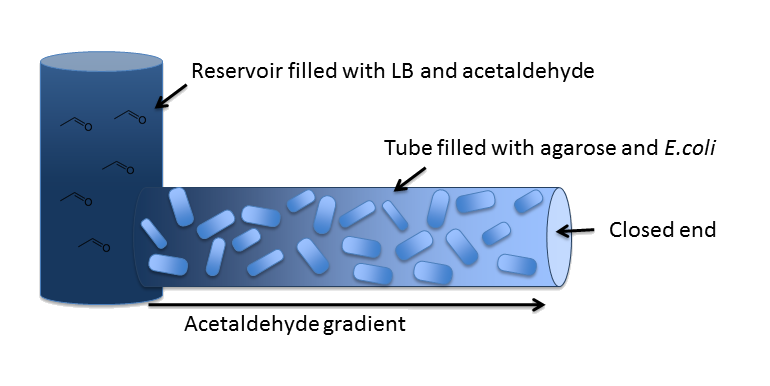
In our inital model, we chose a z_end = 5 cm long cylindrical channel with a radius of R_Channel = 1 mm (or equivalently 2 mm diameter). This channel is connected to a reservoir filled with medium and the toxic molecule. For the purpose of modeling the diffusion and degradation of the toxic molecule in the channel, we assumed that the reservoir has constant toxic molecule concentration (or equivalently has infinite size).

In our system, we degrade a toxic substance diffusing from a reservoir into a block of E. coli cells immobilized in agarose in order to generate a toxic substance gradient. The two substances we consider in our model are acetaldehyde and xylene. In our first microfluidics model we conducted a feasibility study and thus only investigated acetaldehyde degradation.

In general, an acetaldehyde-based reaction-diffusion system for our uniformly SmoColi-filled channel has the following form:

General partial differential equation for an acetaldehyde reaction-diffusion system. D(AcAl(x,z),z) is the diffusive term, R(AcAl(x,z)) is the uniform (independent of the spatial z coordinate) reaction term.

Diffusion

First of all, we have to model diffusion of acetaldehyde from the reservoir to the closed end of the microfluidics channel. The relevant diffusive term is the one for isotropic diffusion, i.e. diffusion that is uniform in all directions:

We assume that the experiment is conducted at pH 7 and 25°C. The relevant diffusion parameter, D_AcAl, is for acetaldehyde diffusion in water at 25°C. However, since the diffusion in our system happens in agarose, we scaled the diffusion constant by a factor C_Agarose.

Note: For parameter values and references click on a parameter or see the microfludics model section on the parameters page.

Degradation

Cell Density

In order to able to determine how much acetaldehyde our smoColi cells are able to degrade, we first need to determine the cell density of the immobilized cells in agarose. For this calculation, we assume we have a cell culture with OD₆₀₀ with which we fill the channel. Parameter-wise, to determine the relative cell density in the channel voume, we need to know:

• the mean cell density in [cells/volume] at OD₆₀₀=1, cd_{OD600, undiluted}, and
• the mean cell volume of a single cell, V_eColi.

A parameter we can choose suitably is the dilution of the cells in agarose, c_Dilution. Then we can calculate the relative cell density cdRel_{OD600, diluted} in the smoColi-agarose-filled microfluidics channel:

Enzymatic Degradation

Now that we know what the cell concentration in the channel is, we can model the degradation of the toxic molecule by the cell culture in agarose. This process, together with diffusion of more toxic molecules from the reservoir, will finally generate the toxic molecule gradient. From here on, we will assume that under laboratory conditions in a closed reservoir, acetaldehyde is stable and thus there is not extracellular degradation of it. It is important to note that this assumption only holds for closed reservoirs, as acetaldehyde evaporates easily and would escape an open reservoir.

In our enzymatic degradation model, we assume diffusion into the cells is fast compared to the degradation process. The degradation process then is modeled using Michaelis-Menten enzyme reaction kinetics:

The constants are the usual ones for Michaelis-Menten-type reactions:

• v_max,AcAl is the maximum reaction rate, i.e. the rate the toxic molecule degradation reaction occurs with at saturation point, and
• K_M,AcAl is the Michaelis Menten constant, i.e. the acetaldehyde concentration at which the reaction rate is half of v_max,AcAl

However, we have to scale the reaction according to the cell density cd_{OD600, diluted}, as not the entire space is filled with cells.

Estimation of v_max,AcAl

For the degradation of acetaldehyde we only had direct literature values for K_M,AcAl, but not for v_max,AcAl. However, we did find values for the specific activity K_cat,AcAl of acetaldehyde dehydrogenase in E. coli, which we used to estimate v_max,AcAl with the following equation:

Here, [E]^T is the total enzyme concentration of acetaldehyde dehydrogenase. This value we derived from the concentration of acetaldehyde dehydrogenase in cell extract, which we in turn calculated by estimating the number of acetaldehyde dehydrogenase enyzmes n_ADH in a single E. coli cell.

The number of acetaldehyde dehydrogenase enzymes n_ADH in a single E. coli cell was estimated from diluted cell-free extract with dilution ratio dil_Extract and diluted concentration of [ADH]_Extract.

Model

Now that we have values for all of the parameters, we can finally combine both the diffusive term and the local reaction term into the spatiotemporal reaction-diffusion (or in our case, degradation-diffusion) system:

Note that in our geometry, the channel extends in z-direction, i.e. the third component of z = ( x, y, z ).

However, we are still missing the initial condition at t=0 and the boundary conditions for both the constant acetaldehyde concentration at the reservoir and the channel walls. We start with the initial condition, which is that there is no acetaldehyde in the agarose-filled channel initially at t=0:

The first boundary condition we consider is the one that enforces constant acetaldehyde at the reservoir, which is located at z = 0 ([http://en.wikipedia.org/wiki/Dirichlet_boundary_condition Dirichlet Boundary Condition]):

Next, we enforce that no transport of acetaldehyde occurs across the channel walls along the channel's axis ([http://en.wikipedia.org/wiki/Neumann_boundary_condition Neumann Boundary Condition]):

Finally, we enforce that no transport of acetaldehyde occurs across the wall at the channel's end ([http://en.wikipedia.org/wiki/Neumann_boundary_condition Neumann Boundary Condition]):

Simulation

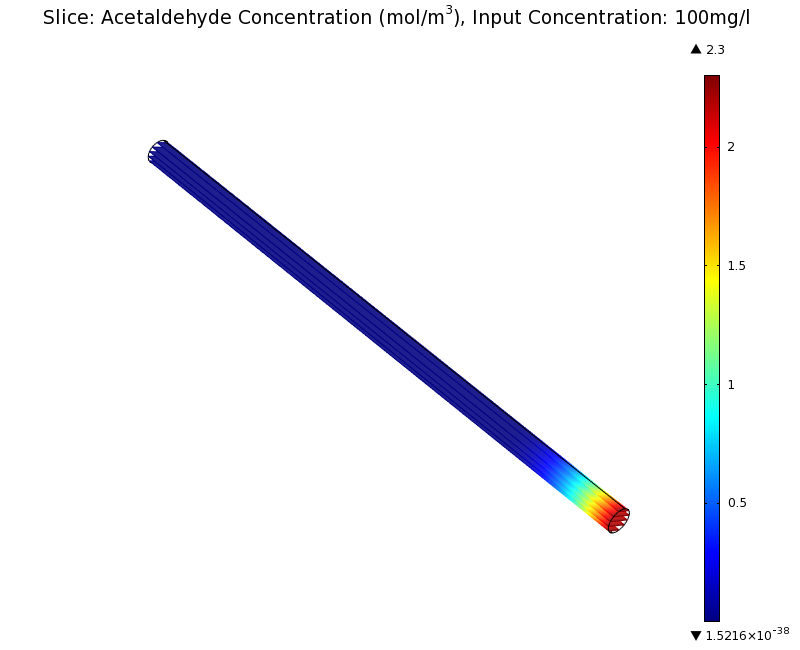
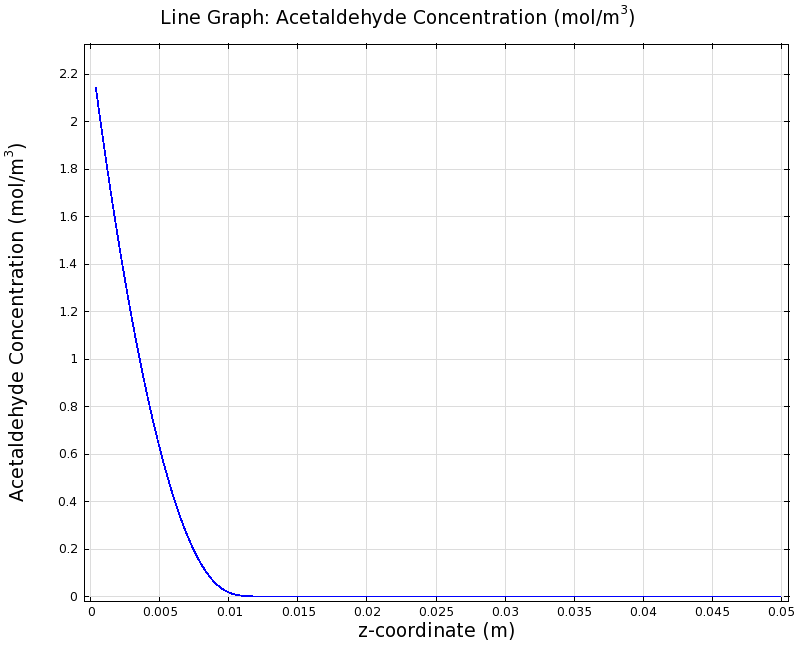
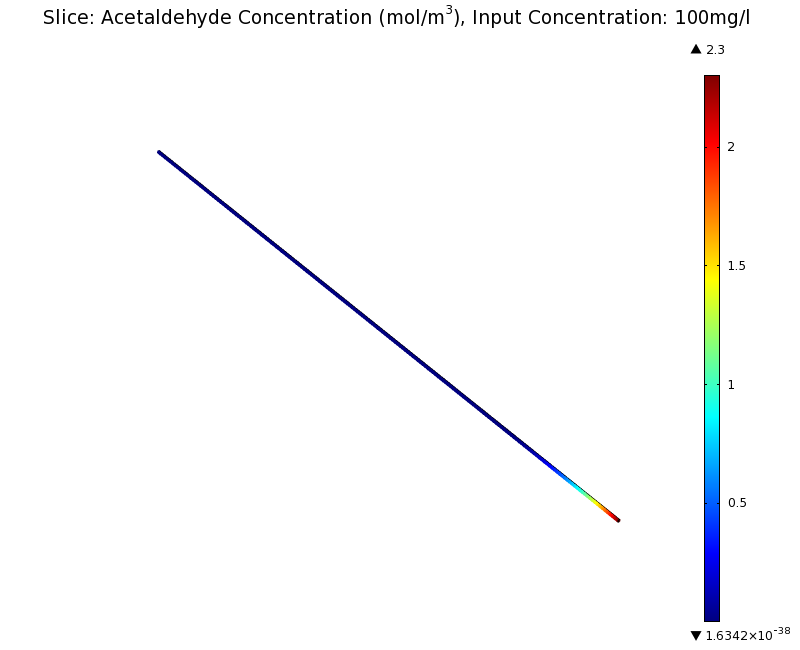
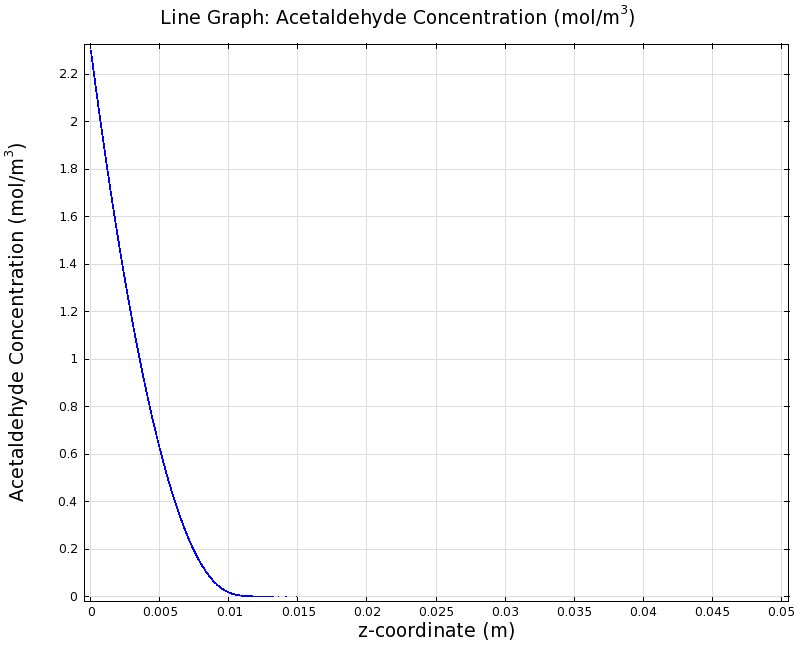
To see if we can indeed create an acetaldehyde gradient, we first solved for the gradient steady state in the channel. We chose an acetaldehyde concentration of 100 mg/l for the reservior in these simulations.

Steady State

Simulation for 100 mg/l of acetaldehyde, standard channel diameter (2mm)

Figure 1: 3D acetaldehyde concentration in mol/m3, 5 slices through the channel. Channel width: 2 mm, reservoir acetaldehyde concentration: 100 mg/l

Figure 2: 1D surface-averaged acetaldehyde concentration in z-axis direction, in mol/m3. Channel width: 2 mm, reservoir acetaldehyde concentration: 100 mg/l

Indeed our SmoColi cells in the model are able to generate a gradient by working (degrading acetaldehyde) against diffusion (which brings in more acetaldehyde). Close to the acetaldehyde input, the degradation mechanism is operating around saturation point, thus the close-to-linear gradient near the input. As more acetaldehyde is degraded further away, the gradient levels off as the degradation mechanism is not running at saturation point anymore.

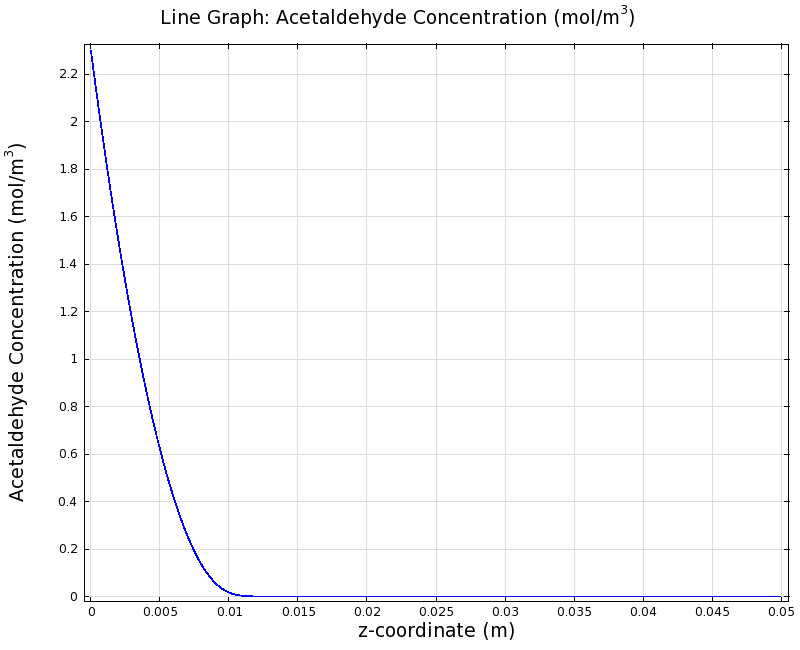
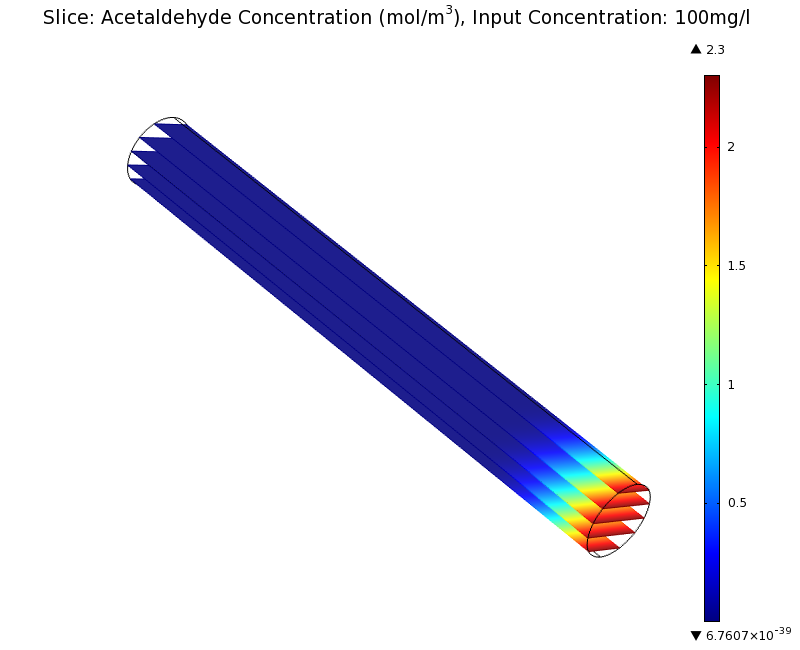
Our belief was that the channel diameter should not change the position of the GFP peak, i.e. that the produced gradient should remain the same for different channel diameters. To verify our intuition, we simulated the steady state of the acetaldehyde gradient in channels with different diameters:

Simulation for 100 mg/l of acetaldehyde, 0.1x standard channel diameter (200μm)

Figure 3: 3D acetaldehyde concentration in mol/m3, 5 slices through the channel. Channel width: 200μm, reservoir acetaldehyde concentration: 100 mg/l

Figure 4: 1D surface-averaged acetaldehyde concentration in z-axis direction, in mol/m3. Channel width: 200μm, reservoir acetaldehyde concentration: 100 mg/l

Simulation for 100 mg/l of acetaldehyde, 3x standard channel diameter (6mm)

Figure 5: 3D acetaldehyde concentration in mol/m3, 5 slices through the channel. Channel width: 200μm, reservoir acetaldehyde concentration: 100 mg/l

Figure 6: 1D surface-averaged acetaldehyde concentration in z-axis direction, in mol/m3. Channel width: 200μm, reservoir acetaldehyde concentration: 100 mg/l

We can see that the diameter indeed does not influence the mean dynamics of the acetaldehyde gradient (observant readers will notice that the concentration at the end of the channel is not exactly the same - this effect is a result of numerical imprecision). We note that there may be irregular behavior for very thin channels, since there will be only very few cells and their local concentration may vary. For the channel diameters we chose above, a mean field approximation should be sufficient though, as the amount of cells involved in the degradation is sufficiently high.

Dynamics

We were also interested in finding out the time scale which is needed to create the gradient. Therefore we also analyzed the dynamics in a spatiotemporal reaction (degradation) - diffusion simulation. As we can see above for the chosen acetaldehyde concentration of this simulation, the gradient primarily is formed in the first 1.5 centimeters of the channel. Therefore, we zoomed in on this part to get a closer look at the dynamics.

We simulated the system for 8 hours in total and now take a look at how long it takes for the gradient to form:

Video 1: 3D gradient formation over 8 hours, starting from zero acetaldehyde in the channel. Display: 3D acetaldehyde concentration in mol/m3, 5 slices through the channel. Channel width: 2 mm, reservoir acetaldehyde concentration: 100 mg/l Press play to start video!

Video 2: 1D gradient formation profile over 8 hours, starting from zero acetaldehyde in the channel, zoomed in on z = [0cm, 1.5cm]. 1D surface-averaged acetaldehyde concentration in z-axis direction, in mol/m3. Channel width: 2 mm, reservoir acetaldehyde concentration: 100 mg/l Press play to start video!

We can clearly see that the gradient converges to steady state after 8 hours and that it only changes very slowly anymore in the last 2 to 3 hours. Thus we deemed diffusion speed of acetaldehyde to not be a limiting factor for experimental design.

Updated Model

In the single-cell model, we noticed that the upper range of detection of our circuit might be toxic to our cells. This lead us to reassess the parameters we assumed in the model. After careful consideration we adjusted some of them to reflect more realistic assumptions as detailed in the toxicity and parameter tuning section of the single-cell model.

This means that the band is created by the bandpass for lower concentrations. However, the degradation mechanism is still the same, thus to avoid toxic concentrations at the input we also should shorten the channel, in our case to 1cm. We then re-ran the simulation of the reaction-diffusion model for the updated geometry, as seen below:

Steady State

Dynamics