Team:Wageningen UR/Project/ModelingProj1

Short repetition of the Hasty construct used as base for our system

For a better understanding of the equations which were used for the modeling of the system, figure 1 shows a short repetition of the circuit published by Danino et al. in the paper [http://www.nature.com/nature/journal/v463/n7279/abs/nature08753.html “A synchronized quorum of genetic clocks”], in our team commonly referred to as the "Hasty construct", which was used as a base for our design.

Fig.1: Basic oscillating genetic circuit as published by Danino & Hasty. [http://www.nature.com/nature/journal/v463/n7279/abs/nature08753.html]

The genes luxI and aiiA can be expressed when a AHL-LuxR complex binds to the promoter region. The circuit uses both a positive and negative feedback loop to control the AHL concentration and therefore the expression of the resulting proteins LuxI and AiiA. In the positive loop, LuxI generates more AHL, which, together with LuxR, can form more of the activating AHL-LuxR complex and therefore stimulates even more production of LuxI and consequently AHL. This complex also activates the expression of aiiA. In the negative feedback loop, AiiA degrades the AHL produced. For more detailed information about the circuit read more about the mechanism in the complete project description.

back to top

Mathematical model of the Hasty construct

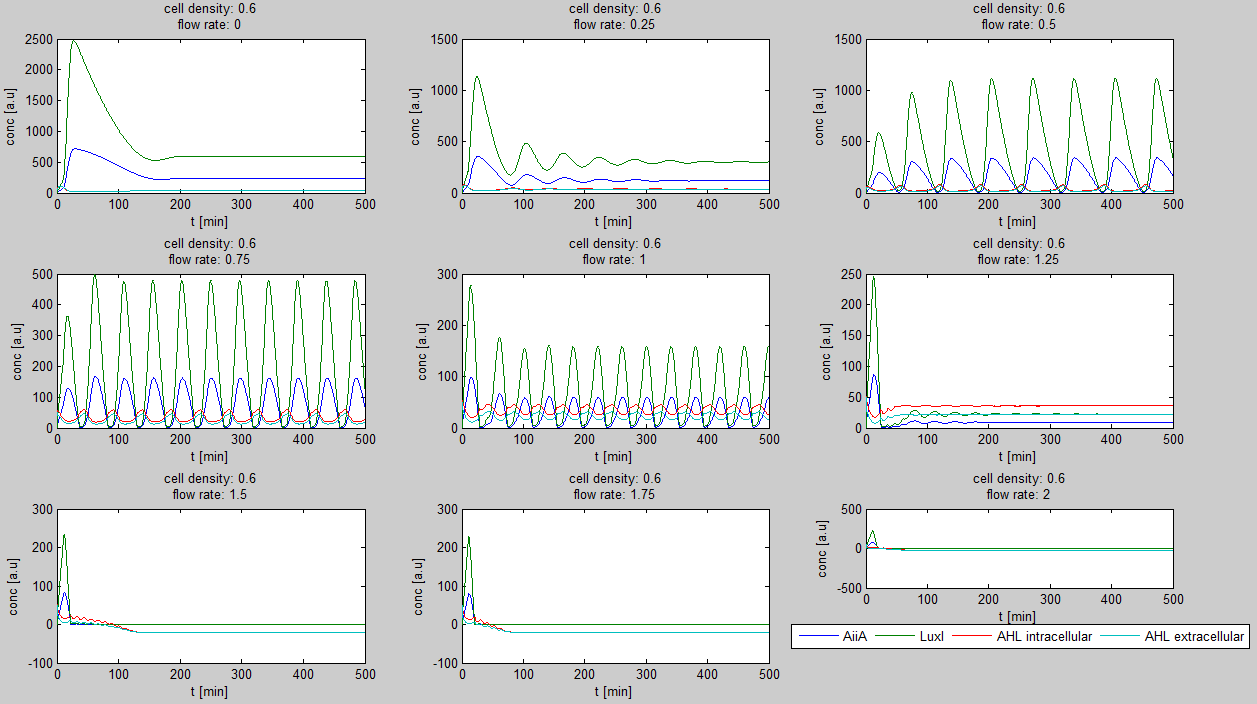
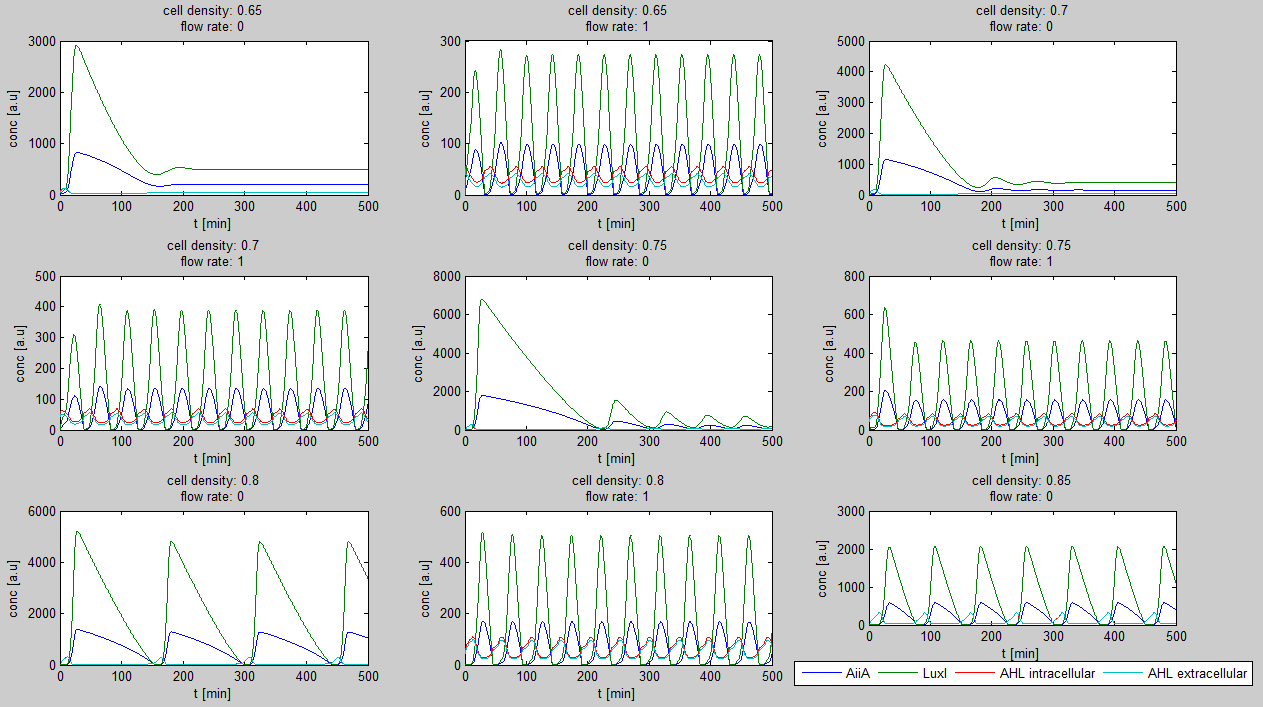
Since our bio bricked oscillatory system is based on the design seen above, our first model of the system is a reproduction of the mathematical model in the [http://www.nature.com/nature/journal/v463/n7279/suppinfo/nature08753.html supplementary information] accompanying the publication mentioned. In their simulations, Danino et al. used the following set of delay differential equations, which we also used as starting point for our modeling work.

left: Set of delay differential equations derived by Danino et al. to model the oscillatory behaviour of the design using a positive and negative feedback loop.

The production of AiiA and LuxI depend on the internal AHL concentration in the single cell. The steps (transcription, translation, maturation etc.) from the luxI and aiiA genes to the corresponding proteins are not modeled separately, but the delay of the correlation between the internal AHL concentration and the corresponding AiiA and LuxI is simulated by the following Hill function:

in which tau represents the time step. It can be seen that the function takes the history of the system into account, since the production of the proteins depend on the past concentration of internal AHL as in: .

back to top

Writing a modeling tool in matlab

Fig.2: GUI of the matlab modeling tool created by team Wageningen UR

For the first simulations, the same values for the parameters were used as in the cited paper and can be found in the [http://www.nature.com/nature/journal/v463/n7279/suppinfo/nature08753.html supplementary information]. To get graphs representing optimal oscillations, our team created a script for a matlab modeling tool which uses nested for-loops to vary the flow rate and cell density over a range of values. The resulting tool allows the user to enter the range in which the variables should be varied. The tool then iterates over the values and plots graphs of all combinations possible for that range of values. Figure 2 shows an example output of the tool.

Fig.2: Variation of output graphs depending on the different starting conditions

back to top

Conclusions for our system

The first observation from the model was that, for oscillations to occur, the flow rates may not be too fast, especially at lower cell densities. Since the device used for our system has larger dimensions than the microfluidic device used by Danino et al. the flow rates in the velocities required could not be achieved by varying height differences alone. Further information can be found in the information about the platform used to measure oscillations.

Furthermore, an interesting observation was that applying a flow rate over the cells was not essential to obtain ocillations. Figure 3 shows how, according to the model, oscillations can potentially occur at 0 flow rate. Interesting is that this happens only at high cell densities.

Fig.3: Graphs showing oscillatory behaviour increasing with cell density even when the flow rate is set to 0

Disregarding the strictly mathematical model, some more conclusions were drawn from modeling work as to whether to use a micro-dish or micro-sieve as platform for measuring oscillations. This is described in more detail in the section about the setup of the device.

Expansion of the model for the double tunable oscillatory construct

To accomodate the idea of the double tunable oscillator, the original set of delay differential equations shown above was expanded by two additional differential equations showing the behaviour of the lacI and tetR repressor. The equations for the LuxI and AiiA production were then expanded by a term showing the influence of the corresponding repressor lacI for LuxI and tetR for Aiia respectively. Below the adjusted set of differential equations is shown.

Top: Adjusted set of differential equations for the double tunable oscillator

Since the lacI repressed hybrid promoter used for this system was designed by the [http://parts.mit.edu/igem07/index.php/Tokyo/Works Tokyo iGEM 2007] team, the equations were derived according to their model. The tetR repressor was then modeled using the same template.

back to top