1. Short repetition of the Hasty construct used as base for our system
For a better understanding of the equations which were used for the modeling of the system, figure 1 shows a short repetition of the circuit published by Danino et al. in the paper [http://www.nature.com/nature/journal/v463/n7279/abs/nature08753.html “A synchronized quorum of genetic clocks”], in our team commonly referred to as the "Hasty construct", which was used as a base for our design.
Fig.1: Basic oscillating genetic circuit as published by Danino & Hasty. [http://www.nature.com/nature/journal/v463/n7279/abs/nature08753.html]
The genes luxI and aiiA can be expressed when a AHL-LuxR complex binds to the promoter region. The circuit uses both a positive and negative feedback loop to control the AHL concentration and therefore the expression of the resulting proteins LuxI and AiiA. In the positive loop, LuxI generates more AHL, which, together with LuxR, can form more of the activating AHL-LuxR complex and therefore stimulates even more production of LuxI and consequently AHL. This complex also activates the expression of aiiA. In the negative feedback loop, AiiA degrades the AHL produced. For more detailed information about the circuit read more about the mechanism in the complete project description.
back to top
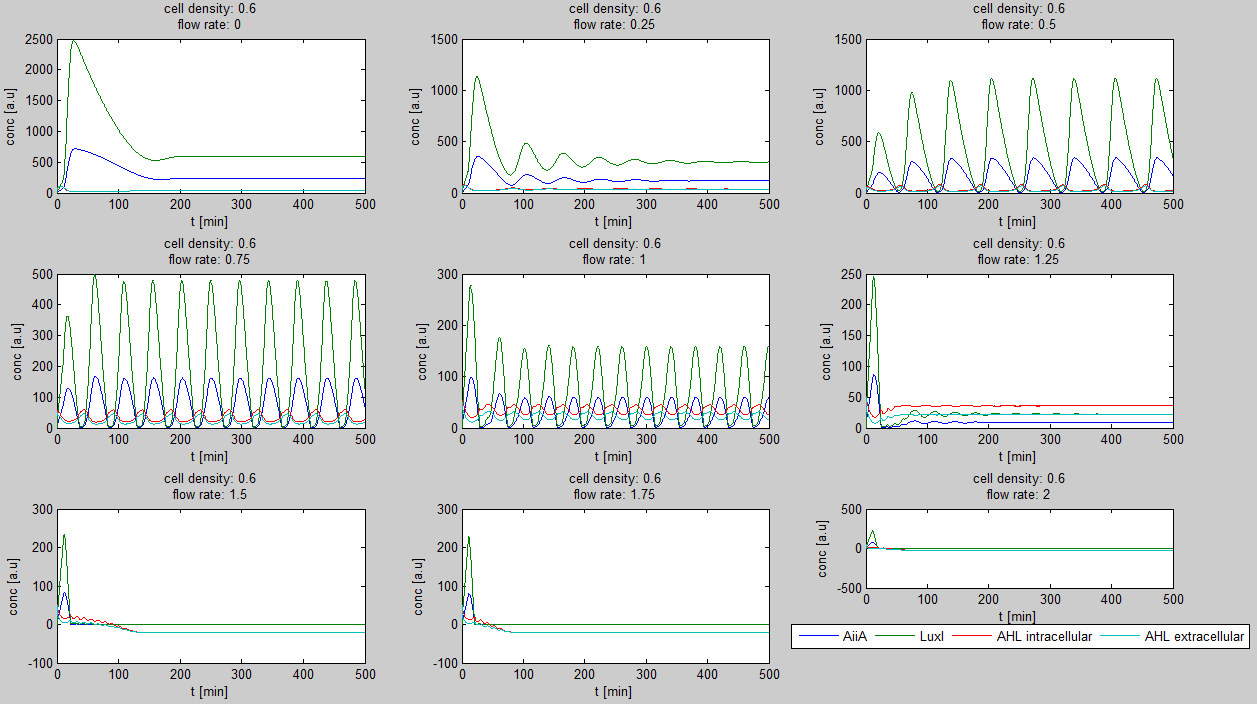
2. Mathematical model of the Hasty construct
Since our bio bricked oscillatory system is based on the design seen above, our first model of the system is a reproduction of the mathematical model in the [http://www.nature.com/nature/journal/v463/n7279/suppinfo/nature08753.html supplementary information] accompanying the publication mentioned. In their simulations, Danino et al. used the following set of delay differential equations, which we also used for our modeling tool written in matlab.
 "
"