Team:NTNU Trondheim/Modeling
From 2011.igem.org

Modeling
To describe and understand the biological reactions and process, as the bacteria turns red under stress we developed multiple mathematical and statistical models. As the most basic model we used a system om ordinary differential equations (ODE), this is a fully deterministic model, describing the change in concentration for all molecules involved. The process for a bacteria to go from normal to glowing red is involved, and one can think of this as a stochastic process, that at each step, the process can ether succeed or fail, with a given probability. This gives rise to a Bayesian model.
Combining these two models will result in a system of stochastic differential equations (SDE), which will be solved using numerical algorithms. As a last model we will explore the relationship between variants of stress and fluoricene intensity using (non)-conventional regression.
Model Introduction
At the heart of the modeling lies biological consistency and data integration. The modeling will be focused on interpretation simplicity and data consistency. That is to develop models that can be easily interpreted by biologist and mathematicians, but the models should also strive to describe that which is observed at the laboratory.
The two main ways to model biological systems. One way is deterministic, the other is stochastic. In this project we will attempt to approach to problems in both ways. Using a deterministic model, with fixed parameters, and a stochastic model to integrate data more dynamically.
Process description
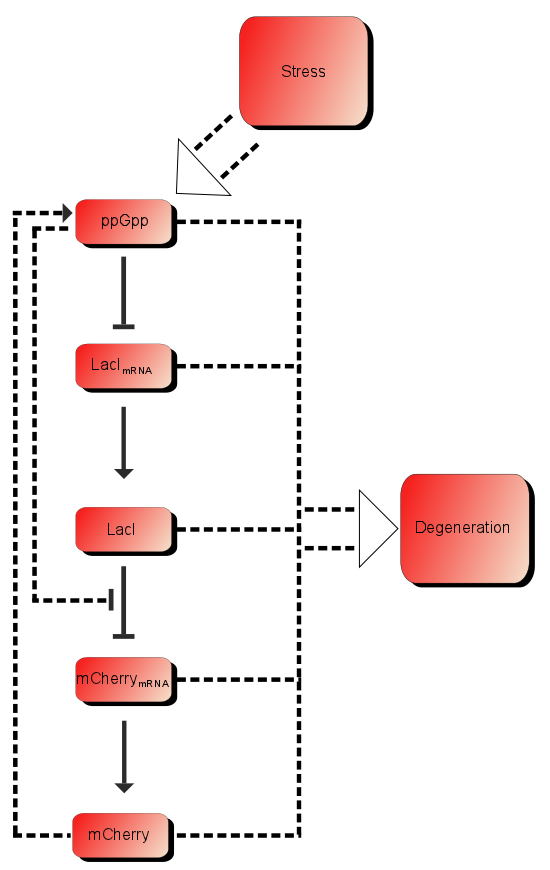
As described in the introduction, ppGpp will repress the production of LacI mRNA which in turn will increase the production of LacI. LacI will in turn repress the production of mCherry mRNA which leads to more mCherry. These are the dominating processes. In short when ppGpp are not present there will be little mCherry, when there are ppGpp rhe level of mCherry will be substantially higher.
In addition to these processes there are additional processes which might be of importance. First of all ppGpp affects the RNAp and can therefore affect the production of mCherry as well as the production of LacI, as described in the introduction LacI is expected to be heavily downregulated by ppGpp. The production of mCherry can also in some cases lead to stress and therefore more ppGpp which in turn leads to more mCherry, in other words a positive feedback loop. These effects are assumed to be small, but might still affect the outcome.
The Models
Four basic models where constructed, which will be described below.
File:ModelAssuptions.pdf File:ModelOvervew.pdf
Systems of ODE
Models based on Ordinary Differential Equations (ODEs) are one of the most used methods of describing genetic cicuits, the different processes and reactions taking place in the cell are described by a set of coupled differential equations. This method might give both qualitative and quantitative information about the system and can therefore be very useful. It is however dependent on accurate kinetic reaction parameters and in some cases one also has to take into account the stochastic nature of genetic circuits. The equations are then solved either in Dizzy or Matlab.
Stochastic Differential equations
In the cell, all movement of the molecules is random, this gives rise to the stochasticity observed in gene expression experiment. In this section we outline two methods where the randomness is accuared for; the Gillespie algorithm and the approximation τ - leap algorithm.
Tau - leap Algorithm
Gillespie
Regression Models
∫
Bayesian Hierarchy
This model did not work properly, and was dropped to concentrate our effort on the other models.
As shown in the introduction, the process before the bacteria turns red is a linear chain of events. This can be modeled as a stochastic process, and solved with Monte Carlo methods. This is a way of including stochastic elements and data integration. Setting the probability of a transition to be successful to be Beta distributed, with hyper parameters ("known constants"), αi and βi, the the probability of total success, that the start input will transcend and cause the output (observable), is the product of all the beta distributed variables, which itself is Beta distributed whit parameter α = ∑ αi-q+1 and β = ∑ βi-q+1, where q is the number of parameters.
Having done some previous test at the lab, we wish to extend this in a probabilistic context. To integrate this data and the model assumptions, we can get a better picture of what is happening in the cell, and how likely it is to succeed in each trail.
Model Validation
No data yet.
References
 "
"