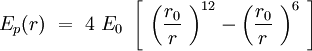"

From 2011.igem.org

When membranes behave like 2D Van der Waals fluids

Trapped between the osmotic pressure and the cell wall, phospholipids are moving in a double layered environment. Their motion is constricted into a two dimensional motion, following the shape of the membrane. At the scale of the phospholipid, the motion can be approximated to a motion in 2D. Using statistical physics approach, we can say that the phase space has 4N dimensions: two dimensions of impulsion and two dimensions of coordinate for each particle (N is the number of particles in the system).

Can we describe the interaction between two phospholipids in the membrane? The question is complicated, but we will demonstrate that by describing properly the phospholipid, as it is reasonable to fit a Lennard-Jones potential energy to this interaction. The energy of binding is smaller and the speed of sliding of one phospholipid against another is slower than the internal vibration of the chemical bounds and the internal conformers rotation of the CH2 tails. Though, in Intermolecular Forces by Israelachvili, the author shows that a phospholipid trapped in a bilayer can be aproximated by a section of cone. The section of cones is an individual, and the others are sections of cone joining the previous one. The shape of the sections are giving the shape of the global structure.

Fig5: Chemical structure of one phospholipid	Fig6: Schematics of the cylindrical approximation made for the phospholipid

Speaking in terms of energy, once we have these cones, it is reasonable to fit a Lennard-Jones potential to this interaction. If the cones are interpenetrating, a steric repulsion keeps the molecules apart, and the hydrophobic interaction that joins one lipid with the other acts as an attractive force keeping the coherence of the membrane. We will discuss later about the value of the two coefficients.

The membrane tension calculation

Considering one membrane a sphere of the radius R, on which the phospholipid double layer is uniformally distributed, we can find approximately a part of the whole sphere surface per one phospholipid :

The caracteristic distance between two neighbor phospholipids on the membrane can be written like this :

where N is the number of phospholipids on the membrane. From this moment on we will work in canonical ensemble. The temperature is fixed and so is the number of particles in the system N. We also consider that the phospholipids can move only on the sphere surface that means that we will study the evolution of our system in 2N dimentional phase space. The partition function will look like :

where the Hamiltonian is :

Knowing the partition function is a great deal. We can derive a free energy

of each sphere, total free energy and the membranian tenstion from it :

For two spheres we get :

and