Team:Sevilla/Modelling
From 2011.igem.org

Wire Kinetics
Our approach to the modeling of our project is centered in the properties of wires. A wire is composed by three elements: EHW, the Emitter Half-Wire, a cell with the hability of produce an arbitrary BioBit i with a spacefic rate; the SINK, a cell with the hability of degradate the BioBit i with a specefic rate and a RHW, the Receptor Half-Wire, a cell that can sense the concentration of i in the culture media and induce gene expresion in response to it. Our project is based in CBW, Chemical-Based Wires, so the BioBit is a chemical compound, in our case, a HSL molecule from quorum sensing, it doesn't matter which one (we also consider the LBW, Light-Based Wires, where a light with a specific spectrum is the BioBit). We are going to assume that the RHW and concentration of i, [i], is solved. We don't want to know the association constant of the molecule to its receptor, but the relation between the concentration of i and the induction of a reporter gene. It would be perfect if we could know the concentration of a BioBit i inferred from the properties of the EHW and the SINK, the two types of cells, in our case bacteria, that are going to define the final concentration of the BioBit i.

The first consideration we must know is: Is our circuit going to run in the exponential phase of growth, or in the stationary phase? We are going to assume that it is going to work in the stationary phase, where the bacterial densities are constants. So, let next equation be the rate of BioBit i production:
Where K_B is the rate of biosynthesis of BioBit i by the EHW and ρ_E is the density of EHW bacteria in the culture, and K_D is the rate of degradation of BioBit i by the SINK and ρ_S is the density of SINK bacteria en the culture. Now, you can see the sequence of calculus until get the primitive:
Now, we assume that the concentration of i(t) at t=0 is i(0) to find the value of the constant:
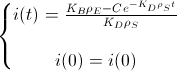
And this is the BioBit i concentration function of time and and taking into account the density of bacteria and the rates of production and degradation of i:
Now, it is interesting if we can get the concentration of BioBit i at equilibrium, this is, when time tends to infinity:
Another interesting thing that we can obtain from that equation is the time it takes to reach a certain fraction α (from 0 to 1) of equilibrium concentration:

So, we have a very interenting equation with great potential but, how can we get the values of the constants of biosynthesis and degradation, and the bacterial densities? The first thing we have to do is to create a cell with a RHW(i) coupled to a reporter gene (lacZ with ONPG, for instance), that is RHW_i>lacZ, and then, we make a messure of reporter activity for some differents concentrations of BioBit i over time:


Now, we have to build another construction to get the behaviour os the EHW, a RHW(j) coupled to the EHW(i):

The experiment is, once you have another verified RWH, RHW(j) in this case, you have to add the enought amount of j bbit to the medium for highest gene expresion, then, measure the reporter signal over time and find the curve that fits with it using the curve for RHW(i). This will let us know Now, if we consider the first part of our initial equation, we can characterize the kinetics of our EHW:
Considering the initial conditions,
The solution of the equation is:
 "
"


